[BASE Cinque - Appunti di Matematica ricreativa]
Ovvero permutazioni con ripetizioni, lineari e cicliche
Beh, se ci pensiamo un po', potremmo concordare che un braccialetto si può vedere da entrambi i lati anche quando è indossato. Quindi si riconosce che è lo stesso visto davanti/dietro, orario/antiorario oppure originale/ribaltato.
Una collana indossata invece si vede da un solo lato perché l'altro è attaccato alla pelle. Se si ribalta, diventa un'altra collana.
Nel calcolo combinatorio di definiscono:
---
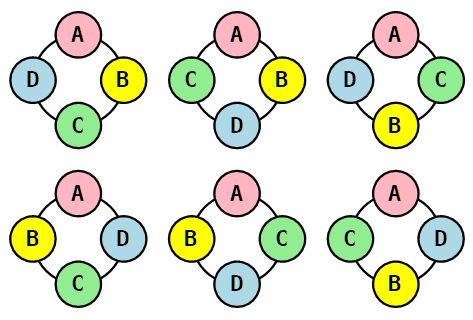
Collana (necklace). Una collana k-aria (o k-adica) di lunghezza n è una sequenza circolare di n oggetti scelti da un insieme di k elementi.
Tutte le rotazioni di tale sequenza in un dato senso (orario o antiorario) sono considerate uguali.
Per esempio:
ABCD = BCDA = CDAB = etc.
Invece due collane di cui una sia il ribaltamento dell'altra NON sono considerate uguali.
Per esempio:
ABCD non è uguale a DCBA
Esistono 6 collane di 4 elementi distinti (4-arie di lunghezza 4).
Sotto le prime tre collane ci sono le rispettive simmetriche, ottenute per ribaltamento.

---
Braccialetto (bracelet). Un braccialetto (o collana libera) è una collana in cui due sequenze sono uguali anche per ribaltamento ovvero quando una è disposta in senso opposto (orario/antiorario) rispetto all'altra. Per esempio:
ABCD = DCBA = etc.
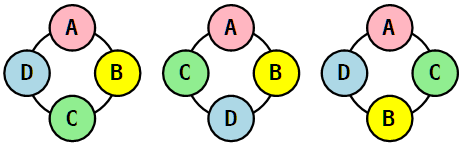
Ci sono solo 3 braccialetti di 4 elementi distinti (collane libere 4-arie di lunghezza 4).
1. Con 4 perline di 4 colori diversi
Supponiamo di avere 4 perline di 4 colori diversi: rosso, giallo, verde, celeste (R,G,V,C).
a) In quanti modi distinti le possiamo disporre in fila?
In pratica si chiede il numero di permutazioni semplici di 4 oggetti distinti.
b) In quanti modi distinti le possiamo disporre lungo una circonferenza per costruire una collana?
In pratica si chiede il numero delle permutazioni cicliche o circolari di 4 oggetti distinti, senza ripetizione.
c) Quanti braccialetti distinti possiamo costruire?
2. Con 6 perline di 2 colori diversi
Supponiamo di avere 6 perline di 2 colori diversi: 3 blu e 3 gialle.
a) In quanti modi distinti le possiamo disporre in fila?
b) In quanti modi distinti le possiamo disporre lungo una circonferenza?
In pratica si chiede il numero delle permutazioni semplici e cicliche di 6 oggetti divisi in due gruppi di 3 oggetti ciascuno, indistinguibili fra loro.
Oppure, le disposizioni di 2 oggetti a gruppi di 6 in cui ogni oggetto è ripetuto esattamente 3 volte.
c) Quanti braccialetti distinti possiamo costruire?
3. Sequenze periodiche di perline colorate
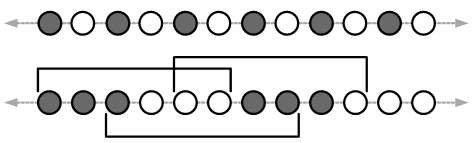
Immaginate una sequenza di perline bianche (B) e nere (N) illimitata in entrambi i versi.
Esistono solo due sequenze distinte di questo tipo nelle quali ogni tratto di 4 perline consecutive contiene esattamente 2 perline bianche e 2 nere.
a) Dimostra che le due sequenze sono del tipo:
...N,B,N,B,N,B,N,B... e
...N,N,B,B,N,N,B,B...

b) Quante sequenze distinte esistono nelle quali ogni tratto di 6 perline consecutive contiene esattamente tre 3 perline bianche e 3 nere?
Ecco due soluzioni abbastanza semplici, ma quante e quali altre se ne possono trovare?
4. Generalizziamo
Come nel caso precedente abbiamo una sequenza illimitata di perline di 2 colori.
a) Quante sequenze distinte esistono nelle quali ogni tratto di 8 perline consecutive ne contenga esattamente tre 4 bianche e 4 nere?
b) Sapreste costruire una formula generale per calcolare il numero delle sequenze in cui 2n perline consecutive ne contengano sempre n bianche ed n nere?
Tratto da un'idea di James Tanton su Twitter.
Nota: le seguenti soluzioni sono appunti da verificare. Non garantite!
1. Con 4 perline di 4 colori diversi
a) Le permutazioni semplici di n oggetti sono n!
24
b) Le permutazioni cicliche sono n!/n ovvero (n-1)!
6
c) ...
2. Con 6 perline di 2 colori diversi
a) Le disposizioni di 6 oggetti di cui 3 di un tipo e 3 di un altro tipo sono:
6! / (3! * 3!) = 20
b) 6 vedi soluzione successiva
c) 3 vedi soluzione successiva
3. Sequenze periodiche di perline colorate
Le sequenze sono tante quante le collane (da verificare ed eventualmente dimostrare).
a)...
b) Ci sono 5 collane e 3 braccialetti distinti. La figura è un esempio.
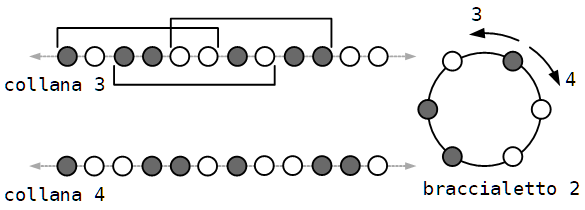
Le soluzioni sono:
Collane 1, 2. Braccialetto 1
aaabbb, bbbaaa
aabbba, bbaaab
abbbaa, baaabb
---
Collane 3, 4. Braccialetto 2
aababb, bbabaa
ababba, babaab
babbaa, abaabb
abbaab, baabba
bbaaba, aabbab
baabab,
abbaba
---
Collana 5. Braccialetto 3
ababab, bababa
4. Generalizziamo
a) ...
b) ...
---
Pace e bene a tutti.
GfBo
Data creazione: giugno 2021
Ultimo aggiornamento: giugno 2021
html5
Sito Web realizzato da Gianfranco Bo