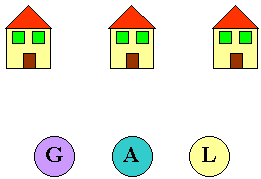
[HOME - BASE Cinque - Appunti di Matematica ricreativa]
Viviamo in un mondo pieno di tori
Sappiamo già che...
...il seguente vecchio problema non si può risolvere su un piano ma si
risolve benissimo sulla superficie di un salvagente (o di una ciambella).
Si devono collegare tre case con tre servizi: acqua, gas ed elettricità.
Disegnate le linee che collegano ciascuna casa con ciascun servizio facendo in
modo che non ci sia nessun incrocio fra le linee.
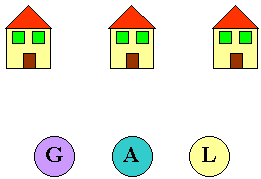
Immaginiamo di vivere su un pianeta a forma di salvagente o
ciambella. Allora potremmo collegare le tre case con i tre servizi senza
difficoltà. I matematici chiamano "toro" la figura geometrica
a forma di ciambella. Non è necessario che sia
perfettamente circolare, basta che abbia il buco.
Si potrebbe obiettare che la Terra non ha la forma di un toro.
Invece vi garantisco che nel pianeta in cui viviamo possiamo trovare centinaia e
forse anche migliaia di tori!
Un esempio è il Monte Forato che si trova nelle Alpi Apuane, in Toscana. E'
formato da due cime gemelle e deve il suo nome al foro naturale aperto nella
cresta che unisce le due cime.

Il Monte Forato (Alpi Apuane) |

L'arco naturale fra le due cime del Monte Forato |
Facciamo un po' di riscaldamento.
Quattro case e tre servizi
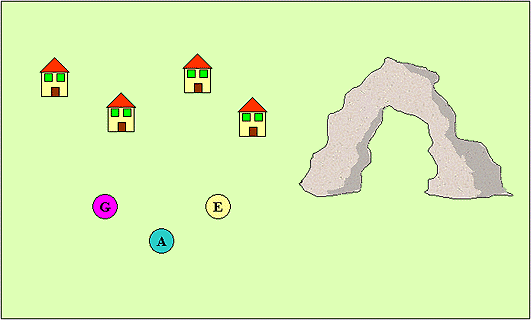
Osservate la figura qui sotto. In una zona pianeggiante si trovano quattro case
e tre servizi, acqua, gas ed elettricità. Nelle vicinanze sorge un arco
roccioso naturale. Disegnate le linee che collegano ciascuna casa con ciascun
servizio facendo in modo che non ci sia nessun incrocio fra le linee.
Ed ecco la vera sfida.
Quattro case e quattro servizi
Lo schema qui sotto è disegnato su un modello di superficie torica.
Disegna le linee che collegano ciascun bollino rosso con ciascun bollino blu
facendo in modo che non ci sia nessun incrocio fra le linee.
Il problema può essere risolto?

Quattro case e tre servizi

Quattro case e quattro servizi
Una soluzione potrebbe essere questa, disegnata su un rettangolo che è il
più semplice modello del toro.

Oppure quest'altra equivalente.

luglio 2004
Sito Web realizzato da Gianfranco Bo