[BASE Cinque - Appunti di Matematica ricreativa]

Passeggiate dei numeri primi

In questo gioco ti propongo di muoverti liberamente in una rete di vie addizionando tutti i numeri che incontri e cercando di realizzare la somma più grande possibile.

Attenzione, però: la somma finale e tutte le somme parziali devono essere numeri primi!

Per risolvere i problemi seguenti è utile la sequenza dei numeri primi da 2 a 139.

2, 3, 5, 7, 11, 13, 17, 19, 23, 29,

31, 37, 41, 43, 47, 53, 59, 61, 67, 71,

73, 79, 83, 89, 97, 101, 103, 107, 109, 113,

127, 131, 137, 139, ...

Passeggiata 1: primi gemelli

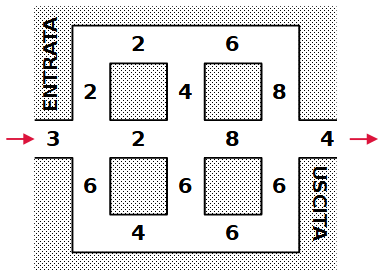
Entra nel labirinto dal numero 3 ed esci dal numero 4 a destra.

Puoi camminare lungo le vie quanto vuoi e guadagnare dei punti.

Ogni volta che passi su un numero, il totale dei tuoi punti aumenta di quel numero.

Cerca di realizzare il massimo numero possibile di punti.

Regole.

1. La somma finale e tutte le somme intermedie dei punti raccolti devono essere numeri primi.
2. E' vietato fare dietro-front.

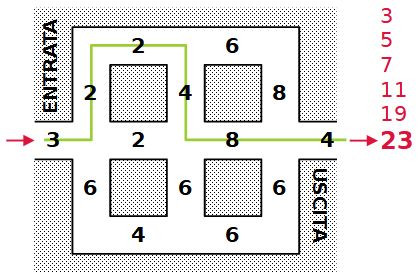
Esempio. La figura mostra un possibile percorso, con l'elenco dei totali parziali, che si conclude con 23 punti. Si può fare di meglio!

Passeggiata 2: primi che distano 10 unità

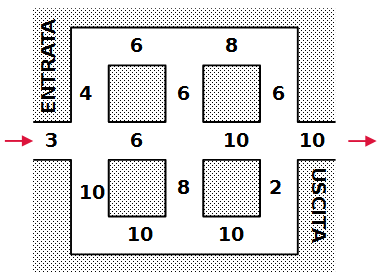
Entra nel labirinto dal numero 3 ed esci dal numero 10 a destra.

Puoi camminare lungo le vie quanto vuoi e guadagnare dei punti.

Ogni volta che passi su un numero, il totale dei tuoi punti aumenta di quel numero.

Cerca di realizzare il massimo numero possibile di punti.

Regole.

1. La somma finale e tutte le somme intermedie dei punti raccolti devono essere numeri primi.
2. E' vietato fare dietro-front.

Domanda bonus

Entra nel labirinto dal numero 3 ed esci dal numero 4 a destra.

Puoi camminare lungo le vie quanto vuoi e guadagnare dei punti.

Ogni volta che passi su un numero, il totale dei tuoi punti aumenta di quel numero.

Regole.

1. La somma finale e tutte le somme intermedie dei punti raccolti devono essere numeri primi.
2. E' vietato fare dietro-front.

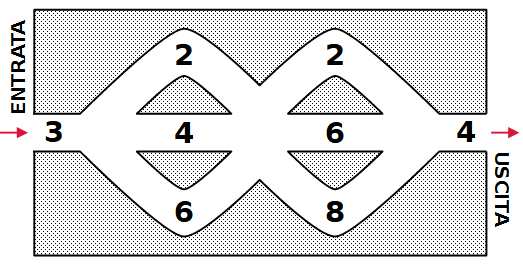
Esempio. La figura seguente mostra un possibile percorso, con l'elenco dei totali parziali, che si conclude con 41 punti.

Un'altra domanda importante.

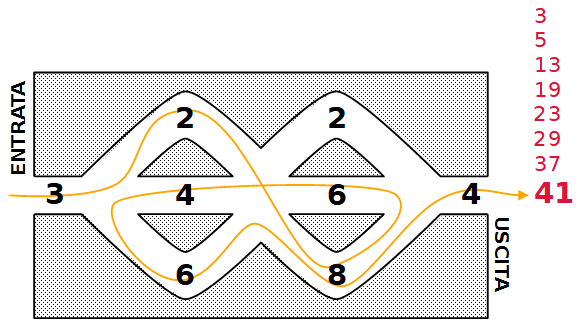
Qual è il MASSIMO punteggio teoricamente realizzabile sui labirinti che ti ho proposto?

Imparare a memoria i numeri primi da 2 a 100

A scuola, dopo aver lavorato un po' con le scomposizioni in fattori primi e le operazioni con le frazioni, ci si accorge di sapere "a memoria" l'elenco dei numeri primi almeno da 2 a 30.

E utile conoscere "a memoria" i numeri primi da 2 a 100?

O per lo meno, esiste un metodo per stabilire a mente e in pochi secondi se un numero di 2 cifre è primo?

Tale metodo esiste.

Vediamo.

• La radice quadrata di 100 è 10.
• I numeri primi minori di 10 sono: 2, 3, 5, 7
• Quindi, se un numero naturale compreso fra 2 e 100 non è divisibile per NESSUNO dei numeri 2, 3, 5, 7 allora è primo.
• Escludiamo subito i numeri pari (maggiori di 2).
• Per i numeri dispari, i criteri di divisibilità per 3 e 5 sono facilissimi.
• Beh, la tabellina del 7 bisogna saperla almeno fino a 7 × 14 = 98.
• Questo metodo funziona con i numeri compresi fra 2 e 120.

Esempi.

Ecco alcuni numeri che "sembrano" primi ma non lo sono:

• 51, divisibile per 3 e 7;
• 57, divisibile per 3 e 19;
• 87, divisibile per 3 e 29;
• 91, divisibile per 7 e 13.

 Invece 97 è primo perché non è divisibile per nessuno dei numeri 2, 3, 5, 7.

Risposte & riflessioni

Passeggiata 1.

Ecco una soluzione buona ma forse si può fare di meglio.

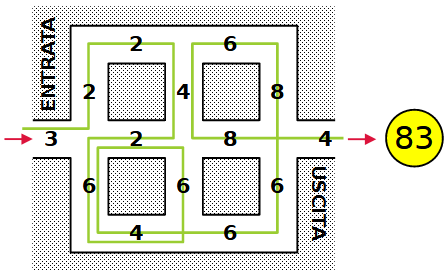
La soluzione si può anche scrivere elencando la sequenza delle somme parziali. Per verificarla occorre un briciolo di attenzione in più.

3, 5, 7, 11, 13, 19, 23, 29, 31, 37, 41, 47, 53, 61, 67, 71, 79, 83.

---

Passeggiata 2.

Ecco una soluzione buona. Se ne possono trovare altre, ma il valore 113 è insuperabile. Perché?

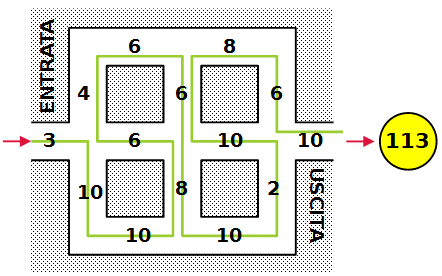
Sequenza delle somme parziali:

3, 13, 23, 31, 37, 41, 47, 53, 61, 71, 73, 83, 89, 97, 103, 113.

---

Domanda bonus.

Beh, con un tragitto abbastanza intricato si può arrivare a 113.

---

Un'altra domanda importante.

Qual è il MASSIMO punteggio teoricamente realizzabile sui labirinti che ti ho proposto?
Il massimo è 113.
Il numero più alto che compare nei grafi è 10, quindi, a qualunque somma parziale si arrivi durante il percorso, non è possibile aumentarla di più di 10 unità.
Ma arrivati a 113, il successivo numero primo è 127, con un salto di 14 unità. Impossibile da raggiungere.

---

Pace e bene a tutti.

GfBo

Data creazione: ottobre 2024

Ultimo aggiornamento: novembre 2024

html5

Sito Web realizzato da Gianfranco Bo