[BASE Cinque - Appunti di Matematica ricreativa]

Un'intuizione aritmetica dantesca, tra Euclide e Hilbert

Tu credi che a me tuo pensier mei
da quel ch’è primo, cosi come raia
da l’un, se si conosce, il cinque e’l sei;

Paradiso, XV, 55-57

Dante immagina che nel Paradiso le anime leggano nel suo pensiero tramite Dio e fa un paragone con la generazione dei numeri naturali a partire dall'unità.

Tu credi che il tuo pensiero si trasmetta (mei) a me tramite Colui che è Primo, così come dalla conoscenza dell'unità deriva (raia = raggiare) quella del cinque e del sei (quindi di tutti gli altri numeri).

L'intuizione di Dante sta in quelle tre parole: "se si conosce".

Solo se conosci l'unità puoi conoscere gli altri numeri che da essa sono generati.

Ma... cos'è l'unità, cos'è il numero 1?

Euclide

Dice Euclide nel libro 7 degli Elementi:

• Def. 1: Unità è ciò in virtù del quale ognuno degli enti è detto uno.
• Def. 2: Numero è una molteplicità composta da unità.

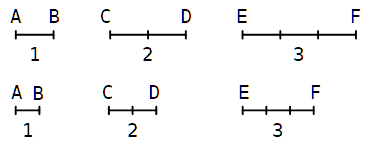
Euclide rappresentava i numeri con segmenti. Puoi conoscere la lunghezza di un segmento solo se sai qual è il segmento preso come unità di misura.

E' quello che facciamo anche oggi quando, per risolvere un problema di geometria, assegniamo a un segmento il valore 1 e troviamo le misure di tutti gli altri segmenti in funzione di quello unitario.

Oppure quando stabiliamo l'unità di misura nelle coordinate cartesiane.

L'aritmetica di Treviso

Quelle due definizioni di Euclide sono diventate una specie di tiritera che è andata avanti per tutto il medioevo e oltre.

Per esempio ne Larte de labbacho o Aritmetica di Treviso del 1478, il primo libro di matematica a stampa pubblicato al mondo, si legge:

L'unità è quella cosa dalla quale ogni cosa è detta una.
Il numero è una moltitudine congregata ovvero insembrada (mescolata?) da molte unità e almeno da due unità, come il 2, che è il primo e più piccolo numero che si trova.

Hilbert

Questa impostazione è arrivata persino a sfiorare David Hilbert, che dice nel Neubegründung der Mathematik (Nuove basi della Matematica) del 1922:

• Das Zeichen 1 ist eine Zahl.
• Ein Zeichen, das mit 1 beginnt und mit 1 endigt, so daß dazwischen
  auf 1 imlmer + und auf + immer 1 folgt, ist ebenfalls eine Zahl, z. B. die Zeichen:
  1+1,
  1+1+1.

Tradotto in italiano, più o meno, è:

• Il segno 1 è un numero.
• Un segno che inizia con 1 e finisce con 1, e nel mezzo, 1 segue sempre + e + segue sempre 1, è anch'esso un numero, per esempio:
  1+1,
  1+1+1.

---

Nel caso di Hilbert, però, la spiegazione è più complessa.

Gli assiomi di Giuseppe Peano

L'approccio di Peano è un'altra variazione sul tema.

Giuseppe Peano, nel libro Arithmetices principia: nova methodo exposita, del 1899, dice (tradotto in linguaggio naturale):

• Spiegazioni.
  Il segno N significa numero (intero positivo).
  Il segno 1 significa unità.
  Il segno a+1 significa il successivo di a.
• Assioma 1. (1 è un numero).
• Assioma 6. (se a è un numero allora il suo successivo è un numero).

L'analisi di Bertrand Russell degli assiomi di Peano

Eh sì, bisognerebbe parlare anche di questo.

In attesa di farlo, rimando al libro Bertrand Russell, Introduzione alla filosofia matematica, Newton, Capitolo 1 - La serie dei numeri naturali.

(Introduction to  Mathematical Philosophy, 1919)

Purtroppo, forse, né Euclide né Hilbert e neppure gli assiomi di Peano rivelano davvero cos'è l'unità e quindi i numeri.

Conclusione?

Conoscere l'unità è quindi un atto mentale meta-matematico?

E perché Dante cita il 5 e il 6 e non il 2 e il 3?

.

---

Pace e bene a tutti.

GfBo

Data creazione: aprile 2021

Ultimo aggiornamento: aprile 2021

html5

Sito Web realizzato da Gianfranco Bo