[HOME - BASE Cinque - Appunti di Matematica ricreativa]

Il triangolo di Dudeney

Questa è una delle più note invenzioni geometriche di Dudeney.
Il problema in sé è abbastanza semplice. E' un classico problema di dissezione.
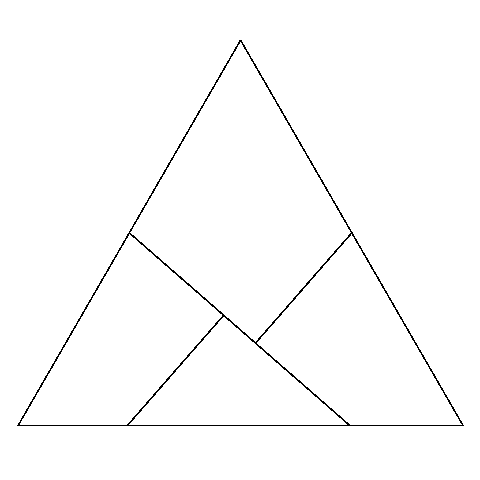
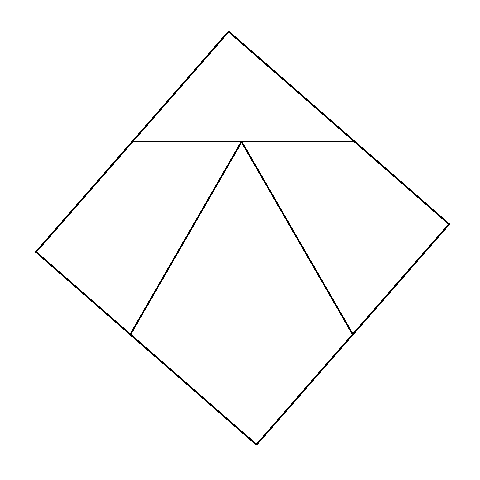
Si chiede di tagliare un triangolo equilatero in 4 parti con le quali si possa costruire un quadrato.
Il quadrato, ovviamente, deve avere la stessa area del triangolo.

Il bello è che i quattro pezzi possono essere fissati l'uno all'altro con tre cerniere in modo da formare una catena che:

a) se si chiude in un verso dà il triangolo equilatero;

b) se si chiude nell'altro verso dà il quadrato.

Risposte & riflessioni

Credo che il problema abbia diverse soluzioni costruibili con riga e compasso.
Qui presento una soluzione particolarmente semplice e facile da capire.

a) ABC è un triangolo equilatero.
b) M, N sono i punti medi di AC e AB.
c) Si traccia BM e si prolunga di MQ = AM.
d) Centrando sul punto medio R di BQ si traccia il cerchio di raggio RQ (blu nella figura).
e) P è il punto in cui il prolungamento di AC dalla parte di A incontra il cerchio BPQ.
f) Centrando su M si traccia il cerchio di raggio M si traccia il cerchio di raggio MP.
g) Tale cerchio incontra il lato BC in D.
h) Su AC si prende il punto E tale che DE = MA
i) Per E ed N si tracciano le perpendicolari EH ed NK a DM.

I segmenti DM, NK, HE dividono il triangolo in 4 parti che possono essere disposte in modo da formare un quadrato.

Dudeney fabbricò un modello in legno di questo puzzle e lo utilizzò per spiegare il problema all'Accademia delle Scienze inglese nel 1905.