[BASE Cinque - Appunti di Matematica ricreativa]

Il calibro aureo (parte seconda)

Perché funziona il calibro aureo e come realizzarne uno digitale da usare sullo schermo del computer

-->Vai alla parte prima

Nella prima parte di questo articolo abbiamo visto come costruire un calibro aureo usando quattro aste di legno. In questa seconda parte risponderemo a due domande:

1. Come e perché funziona il calibro aureo?
2. Come realizzare un calibro aureo digitale, che funzioni sullo schermo del computer?

Aspetti matematici

Per la prima domanda useremo i criteri di similitudine dei triangoli.

Per la seconda attività sfrutteremo una trasformazione geometrica che per gli amici si chiama stiramento. Lo stiramento conserva il parallelismo tra segmenti e i rapporti tra le distanze, anche quando è combinato con le isometrie (es. simmetria, rotazione).
In parole più tecniche, lo stiramento è un caso particolare di trasformazione geometrica affine che si chiama omologia affine ortogonale.
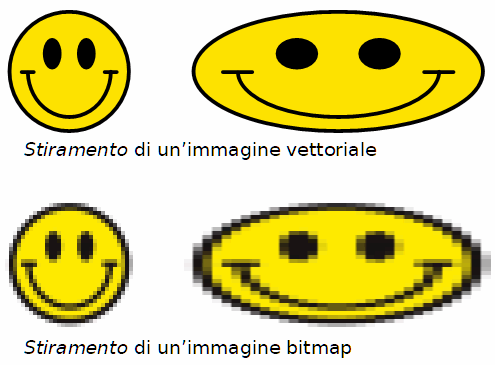
La figura seguente illustra alcuni esempi di stiramento.

Immagine vettoriale vs bitmap

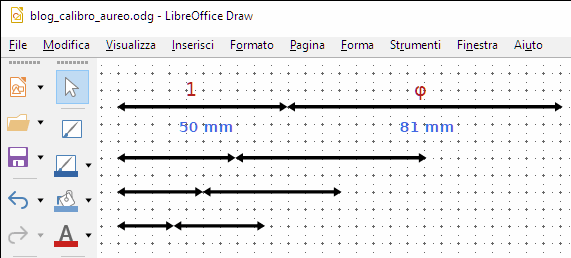
Inoltre disegneremo sullo schermo del computer un calibro aureo con un programma di grafica vettoriale, che in questo caso è Draw di LibreOffice o OpenOffice. Il programma è gratuito e opensource. I programmi di grafica vettoriale assomigliano a quelli di geometria dinamica (come Geogebra) ma sono molto più adatti a fare disegni tecnici e artistici.
Le trasformazioni geometriche delle immagini vettoriali mantengono intatta la loro qualità e non comportano gli sgranamenti tipici delle immagini bimap.

Come e perché funziona il calibro aureo.

Vogliamo costruire un calibro che permetta di misurare i rapporti aurei in una figura o un oggetto.

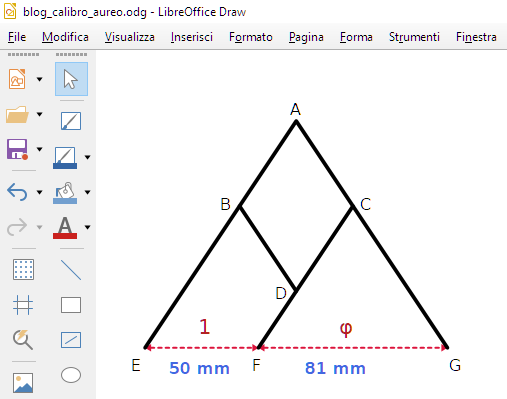
Il calibro dovrebbe essere una specie di compasso proporzionale come quello raffigurato qui sotto. E' formato da 4 aste, AE, AG, BD, CF, snodabili attorno ai punti A, B, C, D,

Se si allarga o stringe l'apertura, il rapporto tra FG e EF dovrebbe essere sempre uguale a φ.

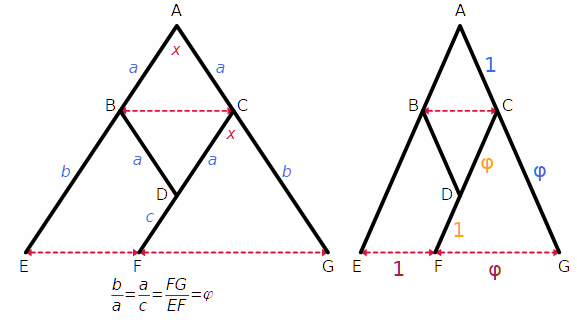
Nella figura:

• le lettere a, b, c, d esprimono le misure dei segmenti;
• in particolare, a + c = b;
• l'angolo x è variabile da 0° a 180°;
• dal fatto che ABDC è un rombo discende che la retta AE è parallela a CF e AG è parallela a BD.

Dobbiamo dimostrare che, variando l'angolo x, il rapporto FG : EF è costantemente uguale al rapporto b : a.

Poi stabiliremo quali valori possono avere a, b, c, affinché tale rapporto sia quello aureo.

Dimostrazione (in sintesi).

1. I triangoli ABC e CFG sono simili, perciò:
   FG : BC = b : a
2. Siccome BC = EF, concludiamo che:
   FG : EF = b : a

La scelta delle misure

Il calibro può essere grande o piccolo a piacere, in base alle misure che vogliamo fare.
In ogni caso il rapporto tra le lunghezze b, a deve essere uguale al rapporto aureo, cioè:

b : a = φ

ovvero:

b = φa

Per esempio, se partiamo da un'asta AG lunga 340 mm otteniamo le seguenti misure, assumendo il valore arrotondato φ = 1,618:

• a + b = 340 mm;
• poiché b = φa,
  abbiamo che a + φa = 340, quindi
  a = 340/(1 + φ) = 129,87 = 130 mm circa;
• b = 340 - a = 210,13 = 210 mm circa;
• c = b - a = 80 mm circa.

Con queste dimensioni possiamo misurare distanze fino a un massimo di:

2(a + b) = 680 mm circa.

La seguente tabella, realizzata con un foglio elettronico, presenta alcuni valori possibili per calibri grandi, medi e piccoli. Le lunghezze sono espresse in millimetri.

Come realizzare un calibro aureo digitale, che funzioni sullo schermo del computer.

Vediamo due metodi. Attenzione, entrambi usano un programma di grafica vettoriale, che in questo caso è Draw di LibreOffice o OpenOffice.

Primo metodo (facilissimo, tempo 1 minuto)

1. Disegnate due segmenti adiacenti lunghi rispettivamente 50 mm e 81 mm (il rapporto fra queste due misure è vicinissimo al rapporto aureo).
2. Impostate le frecce a entrambe le estremità di ogni segmento.
3. Selezionate i due segmenti e usate il comando "raggruppa" in modo da trasformarli in un elemento unico.
4. Ecco finito il calibro aureo.

Potete copiare, incollare, spostare, ruotare, allungare, accorciare, colorare il calibro a vostro piacere. Il rapporto fra i due segmenti che lo compongono rimarrà sempre uguale a φ.

Per usarlo dovete importare un'immagine bitmap nella pagina di Draw e sovrapporre il calibro su di essa, come mostrato qui sotto.
Scoprirete, per esempio, che Leonardo da Vinci (forse) usava il calibro aureo!

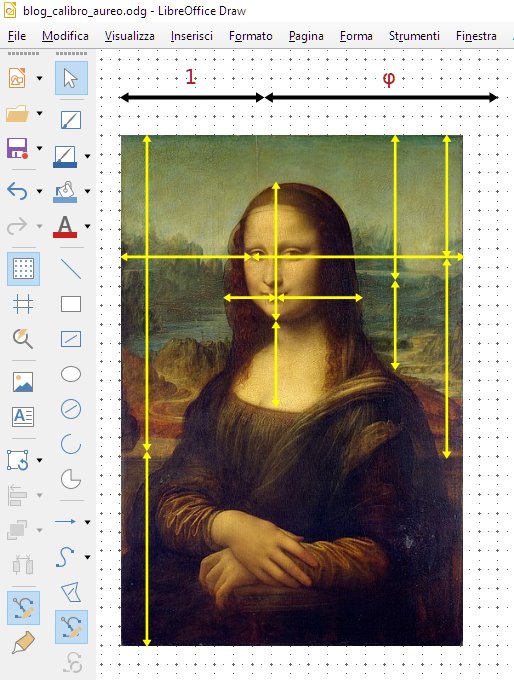
La Gioconda, di Leonardo da Vinci.

Secondo metodo (facile, tempo 5 minuti)

1. Partite con due sementi adiacenti EF, FG lunghi rispettivamente 50 mm e 81 mm come nel disegno precedente.
2. Costruite un triangolo isoscele EAG con AE = AG, alto a piacere.
3. Tracciate per F il segmento FC parallelo ad AE che incontra AG in C.
4. Segnate su AE il punto B tale che AB = AC.
5. Tracciate per B il segmento BD parallelo ad AG che incontra FC in D.
6. Eliminate i segmenti di partenza EF, FG.
7. Selezionate tutti i segmenti rimasti e usate il comando "raggruppa" in modo da trasformarli in un elemento unico.
8. Ecco finito il calibro aureo.

Come nel caso precedente, potete copiare, incollare, spostare, ruotare, stirare, colorare il calibro a vostro piacere. Il rapporto fra le distanze FG ed EF rimarrà sempre uguale a φ.

Per usare il calibro dovete importare un'immagine bitmap nella pagina di Draw e sovrapporlo su di essa, come mostrato qui sotto.

Ho fatto qualche prova sulle Trentasei vedute del Monte Fuji di Katsushika Hokusai. Ecco un esempio.

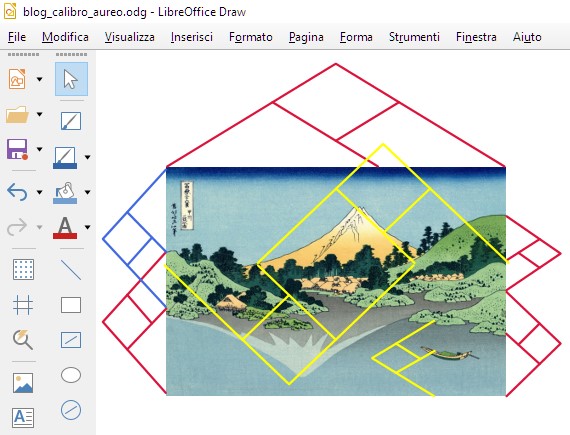
Il Monte Fuji riflesso nel Lago Kawaguchi, visto dal Passo Misaka nella Provincia di Kai, di Katsushika Hokusai

Ho l'impressione che Hokusai NON usi le proporzioni auree oppure le usi in modo complesso, introducendo alcuni piccoli spostamenti.

Questo è un argomento da approfondire...

Data creazione: gennaio 2021

Ultimo aggiornamento: gennaio 2021

html 5

Sito Web realizzato da Gianfranco Bo