[BASE Cinque - Appunti di Matematica ricreativa]

Chiocciola logaritmica

Nel bosco, ho trovato alcune conchiglie di chiocciole. Appartengono alla famiglia delle Elicidi ma quale sarà il genere? Helix, Cepa, Theba, ...?

Si dice che le conchiglie delle chiocciole hanno la forma di spirale logaritmica.

E' vero?

Come si spiega?

Forma e dimensioni

Il diametro di queste conchiglie varia da 1 a 2 cm.

La forma, vista dall'alto è una spirale avvolta in senso orario (partendo dal centro).

Una leggenda narra che una chiocciola su 20.000 è avvolta in senso antiorario, ma io non ne ho mai visto.

Che tipo di spirale è?

Spirale di Archimede e spirale logaritmica

Spirale di Archimede

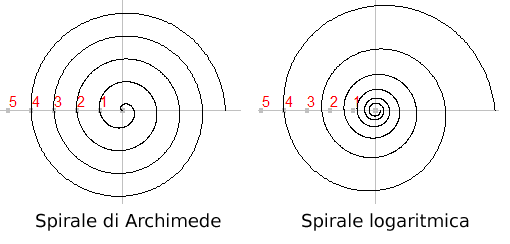
La spirale di Archimede, chiamata anche evolvente, è definita come la traiettoria descritta da un punto che si muove con velocità costante su una semiretta che ruota uniformemente intorno alla propria origine.

Il passo di questa spirale, cioè la distanza fra due spire successive, è costante.

In coordinate polari, l'equazione della spirale di Archimede è:

r(t) = a · t

dove r è il raggio t è l'angolo di rotazione.

Più alto è il coefficiente a, più la spirale è "fitta".

Le equazioni parametriche, invece sono:

x = a · r · cos(t)

y = a · r · sin(t)

Spirale logaritmica

La spirale logaritmica è definita come la traiettoria di un punto che si muove con accelerazione costante su una semiretta che ruota uniformemente intorno alla propria origine.

Il passo della spirale logaritmica, a differenza della spirale di Archimede, non è costante ma cresce secondo una progressione geometrica.

In coordinate polari, l'equazione della spirale di Archimede è:

r(t) = a · e^{b · t}

dove r è il raggio t è l'angolo di rotazione mentre a, b sono due parametri che influiscono sulle caratteristiche della curva.

Le equazioni parametriche, invece sono:

x = a · r · cos(t)

y = a · r · sin(t)

La spirale logaritmica non ha un punto di inizio, ma prosegue indefinitamente sia verso il centro (chiamato polo) sia verso l’esterno.

Che tipo di spirale è quella della chiocciola?

Si nota a prima vista che il passo della spirale cresce ad ogni giro, quindi non può essere una spirale di Archimede.

Una semplice sovrapposizione grafica ci fa notare che la spirale logaritmica si adatta abbastanza bene alla forma della chiocciola, almeno per i primi 5 giri, poi se ne allontana.

Forse, l'accrescimento della chiocciola, a un certo punto, non segue più una progressione geometrica (o esponenziale).

Perché la spirale della chiocciola è logaritmica?

Telegraficamente ipotizzo...

• Le chiocciole (e gli animali in genere) crescono in dimensioni ma mantengono la loro forma.
• La spirale logaritmica ha la caratteristica di mantenere la forma. Ciò significa che se cercassimo di osservare il centro della spirale con una lente d’ingrandimento via via più potente, vedremmo sempre la stessa curva.
• La conchiglia è frutto di un accumulo di parti vecchie e nuove adatte a contenere un organismo che cresce in dimensioni senza cambiare la propria forma.
• Ma come si spiega l'ingrandimento esponenziale della spirale? Probabilmente una nuova sezione della conchiglia si forma quando l'organismo è cresciuto di una determinata percentuale costante rispetto allo stadio precedente.
• Poiché la crescita esponenziale porta in breve tempo a dimensioni troppo grandi, a un certo punto diventa insostenibile perciò rallenta o si ferma.

Data creazione: ottobre 2013

Ultimo aggiornamento: ottobre 2013

html 4.01 strict

Sito Web realizzato da Gianfranco Bo