
[HOME - BASE Cinque - Appunti di Matematica ricreativa]
Un vecchio gioco da Luna Park per spillare soldi alla gente
Questo gioco per me ha un particolare valore: è uno dei primi giochi matematici che ho visto fare nelle fiere tradizionali di almeno 40 anni fa, quando ero piccolo. C'era qualcuno che si guadagnava da vivere con 5 dischi colorati e un banchetto.
Il problema dei 5 dischi
Abbiamo un disco di cartone di raggio 10 cm e cinque
dischi più piccoli di raggio 6,2 cm.
Dobbiamo disporre i cinque dischi piccoli sopra il disco
grande in modo da coprirlo completamente.
Per la precisione il raggio dei dischi piccoli misura 6,180340...cm,
cioè è uguale alla sezione aurea del
raggio del disco grande.

Il problema dei 5 dischi ottimizzato
Risolvere il problema precedente con 5 dischi
piccoli di raggio 6,1 cm.
Per la precisione il raggio è: 6,09382864... cm
Il problema dei 7 dischi
Questa volta il disco di cartone di raggio 10 cm
deve essere interamente ricoperto con 7 dischi di raggio 0,5
cm. Esattamente.
Nota storica.
Non conosco l'origine di questo problema.
La prima soluzione del problema ottimizzato è stata data da
Neville, E. H. in "On the Solution of Numerical
Functional Equations, Illustrated by an Account of a Popular
Puzzle and of its Solution." Proc. London Math. Soc. 14,
308-326, 1915.
Eric Harold Neville (1889-1961) was
a student at Trinity; took the Tripos a year early in 1909 in
order to be in the last of the old-style Triposes, coming in
Second; Smith's Prize, 1911; Fellow of Trinity, 1912. In Jan
1914, he lectured in Madras, acting as Hardy's agent in
arranging for Ramanujan to come to England. Ramanujan stayed
at the Nevilles' house in 113 Chestertown Road for six weeks
on his arrival in Cambridge in April 1914. Neville lost his
Fellowship in 1917, possibly because of his pacifist views.
Tratto da: The British Society for the History of
Mathematics, BSHM Gazetteer
Eric Harold Neville
Neville was Professor of Mathematics 1919-1954. The
collection of his papers includes manuscripts of unpublished
mathematical books; excerpts and offprints; papers relating
to the Indian mathematician Srinivasa Ramanujan 1914 and 1957;
sundry letters 1927-1961; papers relating to the disposal of
his library and other manuscripts. Mathematics books from the
library of Professor Neville, including about 300 pre-1851
works and many later, were added to the Main Library stock,
but are currently being reorganised as a discrete collection.
Secondo David Singmaster la formulazione generale di
questo problema è troppo complessa per poter essere
considerata "ricreativa", e in effetti ha ragione.
Il problema può essere generalizzato così:
Dato un disco di raggio unitario, trovare il più piccolo raggio r(n) che devono avere n dischi uguali per ricoprire completamente il disco di raggio unitario.
Ecco le soluzioni per n che va da 1 a 12.
| n | r(n) |
| 1 | 1 |
| 2 | 1 |
| 3 | sqr(3)/2 |
| 4 | sqr(2)/2 |
| 5 | 0.609382... |
| 6 | 0.555905... |
| 7 | 0,5 |
| 8 | 0.445041... |
| 9 | 0.414213... |
| 10 | 0.394930... |
| 11 | 0.380006... |
| 12 | 0.361103... |
Il problema dei 5
dischi
Abbiamo un disco di cartone di raggio 10 cm e cinque
dischi più piccoli di raggio 6,2 cm.
Dobbiamo disporre i cinque dischi piccoli sopra il disco
grande in modo da coprirlo completamente.
Per la precisione il raggio dei dischi piccoli misura 6,180340...cm,
cioè è uguale alla sezione aurea del
raggio del disco grande.
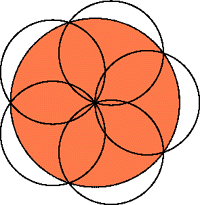
Se si fissa un piano cartesiano con l'origine nel centro del cerchio grande, e si prende come unità il raggio del cerchio grande, allora i centri ci dei cinque cerchi si trovano nei punti di coordinate:

dove f (phi)
è il rapporto aureo e i=1, 2, 3, 4, 5.
(phi-1 = 1/phi = 0,6180339)
Il problema dei 5 dischi ottimizzato
Risolvere il problema precedente con 5 dischi
piccoli di raggio 6,1 cm.
Per la precisione il raggio è: 6,09382864... cm
Nella soluzione si evidenzia la simmetria assiale ma non
quella centrale.

La soluzione di H. Neville
Il problema dei 7 dischi
Questa volta il disco di cartone di raggio 10 cm
deve essere interamente ricoperto con 7 dischi di raggio 0,5
cm. Esattamente.
???
Sito Web realizzato da Gianfranco Bo