[BASE Cinque - Appunti di Matematica ricreativa]

La dimensione frattale

della curva di von Koch

Vi propongo (in riassunto) un problema tratto dal bel libretto di Gilles Dowek, Volete giocare con la matematica?, Barbera editore.

L'albergo sulla spiaggia

Stanno per aprire un nuovo albergo vicino alla spiaggia. L'architetto ha progettato l'albergo intorno a tre spazi: il sentiero (una segmento), la terrazza (un rettangolo) e la costa (una linea frattale).

Si devono lastricare il sentiero, la terrazza e il tratto di costa che è la linea (frattale) di von Koch.

Per il sentiero servono 300 lastre da mettere in fila, una di seguito all'altra.
Per la terrazza servono 700 lastre.
Per la costa servono 1000 lastre.

All'ultimo momento si viene a sapere che l'impresa costruttrice ha soltanto lastre 3 volte più piccole di quelle previste.

Quante di queste lastre serviranno per il sentiero, per la terrazza e per la costa?

Riporto qui sotto la descrizione della curva di von Koch, tratta dal libro di Dowek. che rappresenta la costa, ovvero il confine fra la terra e il mare.

Curva di von Koch

La risposta, relativamente al sentiero e alla terrazza, è facile. Come dice Enrico Delfini al forum:

Leggendo il testo del problema e la triplice domanda, si capisce dove vuole andare a parare l'estensore.

Se si tratta di pavimentare un sentiero (paradigma di grandezza unidimensionale, ci sarà bisogno di n piastrelle x 3.

Se si tratta di una terrazza (bi-dimensionale) ce ne vorranno n x 9.

Per una costa frattale...

Si ricasca comunque nella solita difficoltà semantica. e di rapporto tra "esempio pratico" e "teoria".

Ad esempio: se la linea di costa, o anche il sentiero, è una linea ad una dimensione, e abbiamo a disposizione formelle quadrate, posso usarle in diagonale ? coprendo 1,4142... ad ogni piastrella. o anche di più se ci sono delle curve ! (e nel frattale ce ne sono....)

Dowek spiega così il terzo caso, relativo alla costa.

Per coprire la costa servivano 1000 lastre grandi, ora con lo stesso quantitativo di lastre più piccole si può ricoprire una costa tre volte più piccola.

La costa però è composta da 4 segmenti che formano ognuno una costa ridotta a un terzo.

Occorre perciò un quantitativo quadruplo di lastre, ammontante a 4000 unità.

L'autore poi approfondisce queste considerazioni per dimostrare che la dimensione di Hausdorff della curva di von Koch è log4 / log3.

Chi sa spiegare meglio la soluzione del problema?

Risposte & riflessioni

Ringrazio Enrico, Ivana, Quelo per le illuminanti risposte e i suggerimenti che mi hanno permesso di capire meglio il problema.

In sintesi la risposta è:

piastrelle per il sentiero = 300 x 3 = 900
piastrelle per la terrazza = 700 x 9 = 6300
piastrelle per la costa = 1000 x 4 = 4000

Ho preparato un programmino in Decimal BASIC che illustra vari casi di ricoprimento della curva di von Koch con piastrelle sia circolari, sia quadrate.

Ecco alcuni risultati.

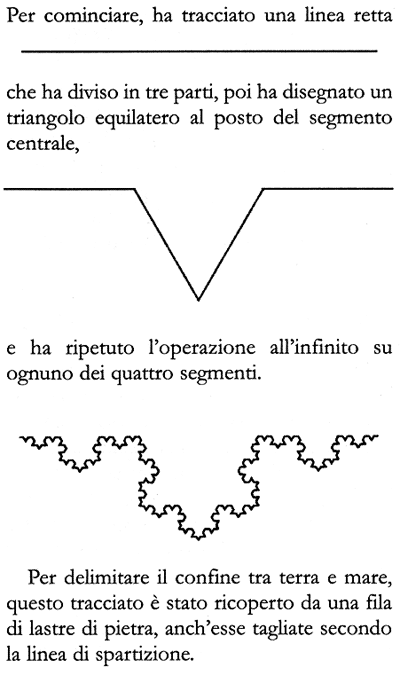
Qual è la piastrella quadrata più piccola con cui posso coprire un segmento rettilineo?

E' quella che ha tale segmento come diagonale.

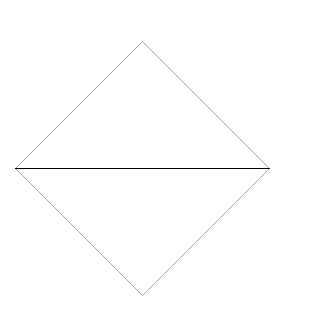
curva von Koch

fig. 1) Koch livello 1

Lo copro con una grande piastrella. La quale copre anche tutti i livelli successivi della curva di von Koch.

Se mi danno piastrelle tre volte più piccole, me ne bastano 3 per coprire il segmento.

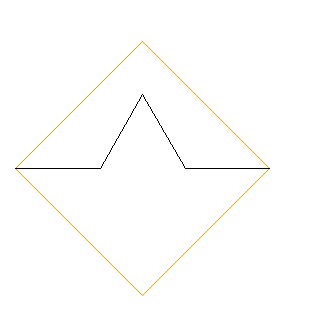
curva von Koch

fig. 2) Koch livello 2

Lo posso coprire con la stessa piastrella di prima...

...ma che succede se ho soltanto piastrelle tre volte più piccole di quella precedente?

Me ne servono 4.

curva von Koch

fig. 3) Koch livello 2

Se ho piastrelle tre volte più piccole (di quelle 4 della figura), e se lo sviluppo della curva frattale si ferma qui, me ne bastano 4 · 3=12.

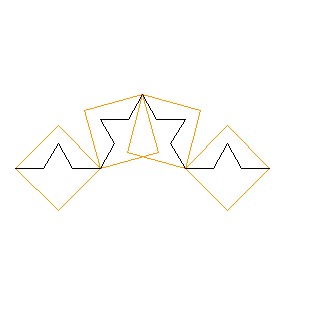
curva von Koch

fig. 4) Koch livello 3

Lo posso coprire con le 4 piastrelle di prima...

...ma che succede se ho soltanto piastrelle tre volte più piccole di quelle precedenti?

Me ne servono 4².

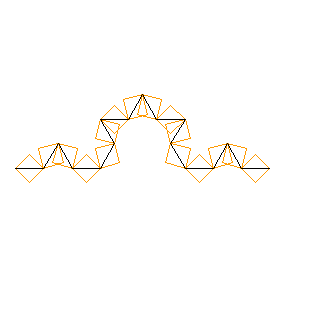
curva von Koch

fig. 5) Koch livello 3

Se ho piastrelle tre volte più piccole (di quelle 16 della figura), e se lo sviluppo della curva frattale si ferma qui, me ne bastano 4² · 3 = 48.

Generalizziamo: Koch livello "infinito"

Lo posso coprire con una grande piastrella...

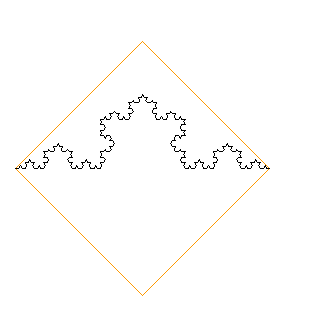
curva von Koch

fig. 6) Generalizziamo: Koch livello "infinito"

... o con 4 piastrelle, 3 volte più piccole...

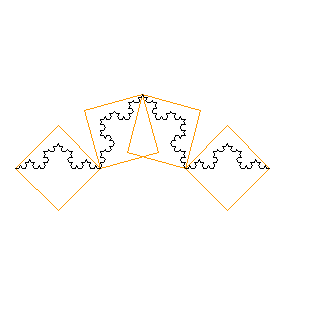
curva von Koch

fig. 7) Koch livello "infinito"

... o con 4² piastrelle, 3² volte più piccole...

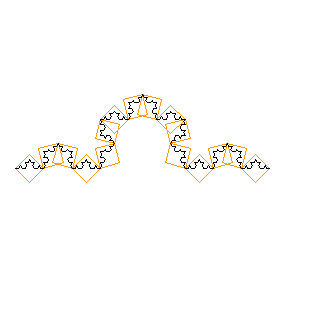
curva von Koch

fig. 8) Koch livello "infinito"

... o con 4³ piastrelle, 3³ volte più piccole... e così via.

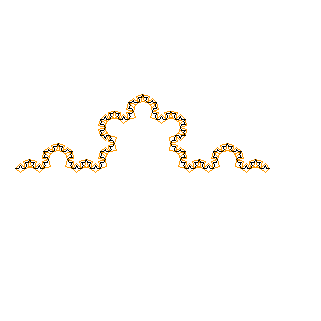
curva von Koch

fig. 9) Koch livello "infinito"

Poiché la curva si suppone generata fino al livello "infinito", il processo non ha termine.

La posso coprire con 4ⁿ piastrelle, 3ⁿ volte più piccole rispetto alla grande piastrella iniziale.

Inoltre, in qualunque stadio mi trovo, se uso piastrelle tre volte più piccole, me ne servono il quadruplo.

Questo perché la curva è generata fino al livello "infinito" (che però non riesco a immaginare).

Ok, ma come si collega questo fatto con la dimensione frattale (di Hausdorff?)?

tipo di figura	numero di piastrelle di diametro D che servono per ricoprirla	numero di piastrelle di diametro D/p (cioè p volte più piccole di quelle precedenti) che servono per ricoprirla	numero di dimensioni della figura
linea	n	N = p¹ · n	dim. topologica = 1
superficie	n	N = p² · n	dim. topologica = 2
solido	n	N = p³ · n	dim. topologica = 3
curva di von Koch	n	N = p^d · n	dim. topologica = 1 dim frattale = log4/log3 = 1,26...

Osservando la tabella possiamo dire che il numero di dimensioni di un oggetto è l'esponente d da dare a p nelle espressioni:

N = p^d·n

Nel caso della curva di von Koch, abbiamo:

N = n·4ⁿ

n = n

p = 3ⁿ

e possiamo quindi scrivere:

n·4ⁿ = 3ⁿ·d

n·log4 = n·d·log3

d = log4 / log3

Nota 1.

Il ricoprimento con "sfere" o dischi, può avvenire anche in modo irregolare, come illustrato nella figura seguente.

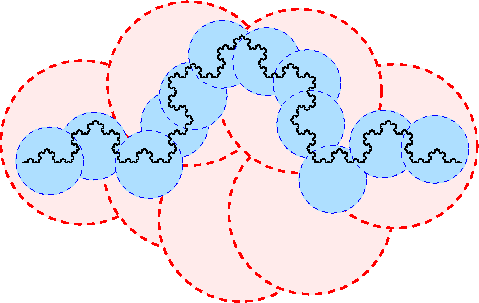
curva von Koch

Nota 2 (tratta dal testo La dimensione frattale di Luciano D'Alessio, Dipartimento di Chimica, Università della Basilicata - Corso di formazione per insegnanti di scienze, 18-25 maggio 2006)

La dimensione frattale di un oggetto rappresenta allo stesso tempo il grado di irregolarità, la capacità di riempimento dello spazio e il livello di autosomiglianza. Quest'ultimo concetto é ben evidente in alcune figure classiche della geometria frattale, come la polvere di Cantor, la curva di von Koch e il triangolo di Sierpinski.

In questi casi la dimensione frattale può essere calcolata facilmente con l'equazione:

d = ln(N)/ln(S)

in cui N è il numero delle parti autosimili, in cui un oggetto può essere suddiviso,

ed S é il fattore di scala per cui bisogna moltiplicare ciascuna delle

parti per sovrapporla al tutto. Questa equazione fornisce per i tre oggetti

mostrati sopra i seguenti valori:

Polvere di Cantor: d = ln 2/ln 3 = 0.63
curva di Koch: d = ln 4/ln 3 = 1.26
Triangolo di Sierpinski: d = ln 3/ln 2 = 1.58

Oggi il termine frattalità é sinonimo oltre che di dimensionalità frazionaria, anche di irregolarità a tutte le scale, di complessità, di autoreferenzialità ed S é il fattore di scala per cui bisogna moltiplicare ciascuna delle

parti per sovrapporla al tutto. Questa equazione fornisce per i tre oggetti

Nota 3 (tratta dal sito www.frattali.it, a cura di Claudia Lotti).

Un altro modo di caratterizzare un frattale è quello di definirne la dimensione.

Infatti, un frattale si può definire come un oggetto a dimensione frazionaria.

Il concetto di dimensione di un oggetto è abbastanza familiare. Ad esempio un segmento ha dimensione 1, un quadrato ha dimensione 2 ed un cubo ha dimensione 3. Cerchiamo ora di dare una definizione più rigorosa al concetto di dimensione. Per fare questo useremo la definizione di autosimilarità.

Ricordo che un oggetto è autosimile quando può essere diviso in un certo numero di parti simili alla figura intera.

Ad esempio:

un segmento può essere diviso in N parti simili al segmento intero, ciascuna parte di lunghezza 1/ N;
un quadrato può essere diviso in N² parti simili al quadrato intero. Ciascuno di questi quadratini più piccoli avrà area pari a 1/N² del quadrato grande;
un cubo può essere diviso in N³cubi più piccoli; ciascuno avrà volume pari ad 1/ N³ del cubo iniziale.

In questi casi la dimensione è data dall'esponente di N.

Vediamo la definizione generale. Supponiamo di considerare un frattale in cui possiamo distinguere N copie autosimili. Ciascuna di queste copie si ottiene tramite un'omotetia di rapporto K. La dimensione frattale D è definita nel seguente modo:

D = log N / log (1/K)

Nei tre esempi visti sopra K = 1/N. Di conseguenza otteniamo:

D(segmento) = log N / log(N) = 1;
D(quadrato) = log(N²) / log(N) = 2;
D(cubo) = log(N³) / log (N) = 3.

Se applichiamo questo procedimento al triangolo di Sierpinski, otteniamo:

curva von Koch

D = log 3 / log 2 = 1,585

Infatti, il triangolo di Sierpinski può essere diviso in 3 parti simili all'intero triangolo. Ciascuna di esse si ottiene grazie ad un'omotetia (ingrandimento o riduzione in scala) di rapporto K=1/2.

Considerando invece la curva di von Koch, otteniamo:

curva von Koch

D = log 4 / log 3 = 1,262

Infatti, la curva di von Koch può essere divisa in 4 parti simili all'intero frattale. Ciascuna di esse si ottiene grazie ad un'omotetia di rapporto K=1/3.

In entrambi i casi si tratta di numeri frazionari compresi fra 1 e 2. Possiamo dire che la dimensione ci dà un'idea di quanto il frattale riempia il piano. Frattali di dimensione prossima ad 1 saranno simili ad una curva, frattali di dimensione prossima a 2, tenderanno ad occupare tutto il piano.

Nota 4.

Questo è il programma in Decimal BASIC che ho utilizzato per fare i disegni.

!'Disegna un cerchio di centro e raggio dati

PICTURE circle(cx,cy,r)

SET LINE COLOR 56

PLOT cx, cy

LET st=PI/180

FOR i=0 TO 2*PI STEP st

PLOT LINES: cx+r*COS(i),cy+r*SIN(i);

NEXT i

SET LINE COLOR 1

END PICTURE

!'Disegna un quarato dati gli estremi della diagonale

PICTURE quad(x1,y1,x2,y2)

SET LINE COLOR 56

LET cx=ABS(x1+x2)/2

LET cy=ABS(y1+y2)/2

LET diag=SQR((y2-y1)^2+(x2-x1)^2)

LET lato=diag/SQR(2)

LET ang=ATN((y2-y1)/(x2-x1))

LET x3=cx+diag/2*COS(ang+PI/2)

LET y3=cy+diag/2*SIN(ang+PI/2)

LET x4=cx+diag/2*COS(ang-PI/2)

LET y4=cy+diag/2*SIN(ang-PI/2)

PLOT LINES: x1,y1;

PLOT LINES: x3,y3;

PLOT LINES: x2,y2;

PLOT LINES: x4,y4;

PLOT LINES: x1,y1

SET LINE COLOR 1

END PICTURE

!'Disegna la curva di von Koch con i seguenti parametri:

!'lev = 1, 2, 3, 4, 5, ...livello

!'lin = 0,1, traccia le linee sì/no

!'cir = 0,1, traccia un ricoprimento di cerchi sì/no

!'quad = 0,1, traccia un ricoprimento di quadrati sì/no

!'t()

SUB koch(lev,lin,cir,quad,t())

SET WINDOW -1,20, -10,11

LET contcol=1

SET LINE COLOR contcol

LET scala=50

LET a=lev

LET p = a

LET h = 3 ^ (-p)

IF lin=1 THEN PLOT LINES: 0, 0;

LET x=0

LET y=0

FOR n = 0 TO 4 ^ (p - 1)-1

!'Cambia colore ad ogni sezione

'IF n/(4^2) = INT (n/4^2) THEN

' LET contcol=contcol+1

' SET LINE COLOR contcol

'END IF

LET m = n

FOR l = 0 TO p - 1

LET t(l) = MOD(m , 4 )

LET m = INT(m /( 4 ))

NEXT l

LET s = 0

FOR k = 0 TO p - 1

LET s = s + MOD((t(k) + 1) , 3 ) - 1

NEXT k

LET xv=x

LET yv=y

LET x = x + scala*COS(PI * s / 3) * h

LET y = y + scala*SIN(PI * s / 3) * h

IF lin=1 THEN PLOT LINES:x, y;

!'Cerchi

!'Centro

LET cx=ABS(xv+x)/2

LET cy=ABS(yv+y)/2

!'Raggio

LET r=SQR((xv-x)^2+(yv-y)^2)/2

IF cir=1 THEN DRAW circle(cx,cy,r)

IF cir=1 THEN PLOT LINES: x,y;

IF quad=1 THEN DRAW quad(xv,yv,x,y)

IF quad=1 THEN PLOT LINES: x,y;

NEXT N

END SUB

!'programma principale

!'Per ottenere un disegno è sufficiente chiamare la funzione

!' call koch(lev,lin,cir,quad,t())

!'Demo

OPTION BASE 0

DIM t(200)

!'Ricoprimento con cerchi

FOR lev1 = 1 TO 5

FOR lev2 = 1 TO lev1

SET DRAW MODE HIDDEN

CLEAR

!'Disegna un ricoprimento

CALL koch(lev2,0,1,0,t)

!'Disegna le linee

CALL koch(lev1,1,0,0,t)

SET DRAW MODE EXPLICIT

WAIT DELAY 1

NEXT lev2

NEXT lev1

!'Ricoprimento con quadrati

FOR lev1 = 1 TO 5

FOR lev2 = 1 TO lev1

SET DRAW MODE HIDDEN

CLEAR

!'Disegna un ricoprimento

CALL koch(lev2,0,0,1,t)

!'Disegna le linee

CALL koch(lev1,1,0,0,t)

SET DRAW MODE EXPLICIT

WAIT DELAY 1

NEXT lev2

NEXT lev1

END

Data creazione: giugno 2008

Ultimo aggiornamento: giugno 2008

xhtml 1.1

Sito Web realizzato da Gianfranco Bo