[HOME - BASE Cinque - Appunti di Matematica ricreativa]
Puzzles paradossali facili da costruire, un po' più difficili da spiegare
Da 8x8 a 5x13
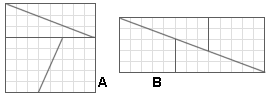
Le due figure qui sotto sono formate dagli stessi
pezzi disposti in un ordine diverso.
La prima figura è un quadrato di area 8x8=64
La seconda è un rettangolo di area 13x5=65
Come si spiega?

Dove si è perso il quadratino?
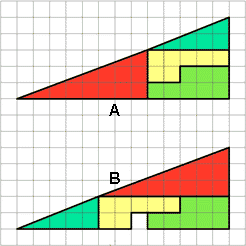
Le due figure qui sotto sono formate dagli stessi
pezzi disposti in un ordine diverso.
La prima figura è un triangolo rettangolo di area 13x5/2=65/2
La seconda è un triangolo rettangolo di area 13x5/2=65/2
Eppure è evidente che nella seconda figura manca un
quadratino.
Come si spiega?
Quattro quadratini scomparsi!
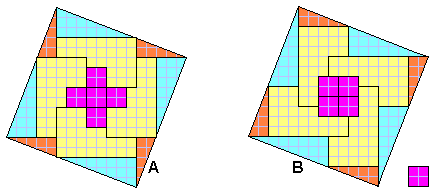
I due quadrati qui sotto sono uguali e sono formati
dagli stessi pezzi disposti in un ordine diverso.
Eppure è evidente che nella seconda figura mancano ben 4
quadratini.
Dove sono finiti?
Nota storica.
Loyd, Cyclopedia, 1914, pp. 288 & 378. Da 8 x
8 a 5 x 13
Una buona discussione
delle evanescenze geometriche si trova nel libro di Martin
Gardner, Mathematics, Magic and Mistery, del 1956.
Da 8x8 a 5x13
Nella figura B la diagonale è una linea ingannevole.
Per come è costruita la figura A, non può essere un solo
segmento di retta.
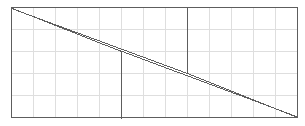
In realtà, come si vede nella figura qui sotto, sono 4
segmenti che formano un parallelogrammo talmente schiacciato
da poter essere confuso con una linea abbastanza spessa.
L'area del parallelogrammo corrisponde proprio al quadratino
in più.
Dove si è perso il quadratino?
Quattro quadratini scomparsi!
Sito Web realizzato da Gianfranco Bo