[BASE Cinque - Appunti di Matematica ricreativa]

Inviluppo della parabola

Grazie a Info per aver postato questo problema al Forum e a gnugnu per i contributi alla discussione e alle soluzioni.

La discussione nel Forum è intitolata Coordinate di un rombo.

Chi non ha mai fatto disegni come questo?

Figura 1.

Qual è la regola per tracciare questo tipo di disegni?

Potete fare così, con riferimento alla figura 1:

• disegnate un quadrato di lato lungo a (per esempio 10 cm);
• dividete due lati consecutivi di un quadrato in 10 parti uguali;
• numerate i punti di divisione da 0 a 10;
• collegate con un segmento il punto 0 del lato orizzontale con il punto 10 del lato verticale;
• procedete allo stesso modo collegando successivamente le coppie 1-9, 2-8, 3-7, 4-6, e così via fino a 9-1.

Usando le coordinate cartesiane possiamo dire, in generale, che tracciamo i segmenti che collegano i punti (0;x) e (a-x;0) con:

• a = lato del quadrato;
• 0≤x≤a (x che varia fra 0 e a)

Se facciamo una suddivisione via via più fitta, otteniamo delle figure come quella qui sotto.

Figura 2.

La figura è formata soltanto da linee rette ma si forma una linea di confine evidentemente curva.

Tale linea separa la parte del quadrato che contiene le linee rette dalla parte che non ne contiene.

Che tipo di linea è?

In questo caso è un arco di parabola.

Per la precisione, la parabola ha il fuoco nel centro del quadrato e il vertice nel punto medio tra il fuoco e il vertice del quadrato che si trova nell'origine degli assi.

L'inviluppo

Le infinite rette che si possono tracciare seguendo la regola indicata sono tutte tangenti a una unica parabola.

In linguaggio matematico possiamo dire che una famiglia di rette inviluppa una curva se ogni retta della famiglia è tangente alla curva stessa.

In altri termini possiamo anche dire che la curva (nel nostro caso la parabola) è l'inviluppo della famiglia di rette.

La seguente animazione rende bene l'idea.

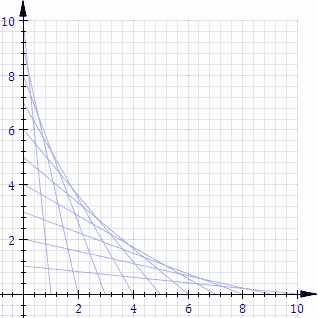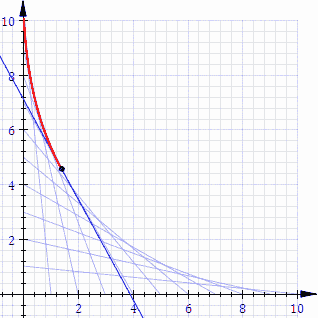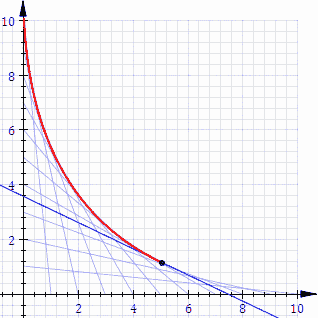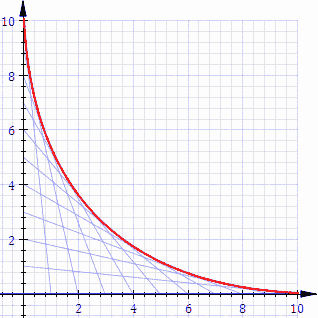
Credit: Wikipedia

Come si calcola l'equazione della curva di inviluppo?

Da approfondire...

Per me, un metodo abbastanza semplice è quello di usare le curve di Bezier quadratiche per arrivare con pochi passaggi alle seguenti equazioni parametriche:

x=t²

y=(1-t)²

con 0≤t≤1

Giochiamo con le tangenti

Se ripetiamo lo stesso procedimento su tutti i lati del quadrato otteniamo la seguente figura.

E' bella esteticamente ed è interessante matematicamente.

Figura 3.

Che quadrilatero è quello tracciato in rosso?

E' un quadrato.

Più avanti sarà chiaro il perché.

Quali sono le coordinate dei suoi vertici?

Se assumiamo che il lato del quadrato sia lungo 1 (una unità) e sempre facendo riferimento alla figura 3:

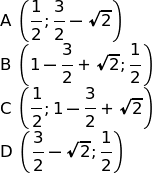
Se invece il lato del quadrato grande è diverso da 1, allora tutte le misure cambiano in proporzione.

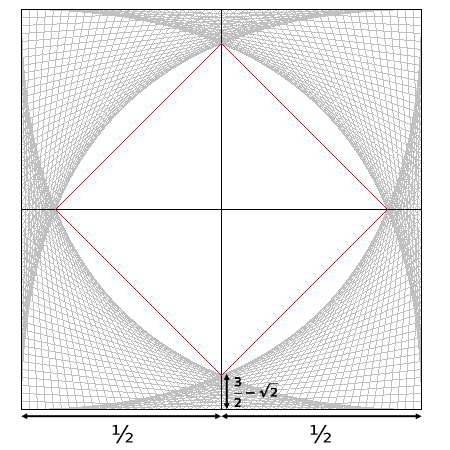
Figura 4.

Come si possono calcolare matematicamente le coordinate dei suoi vertici?

Osservate la figura 5.

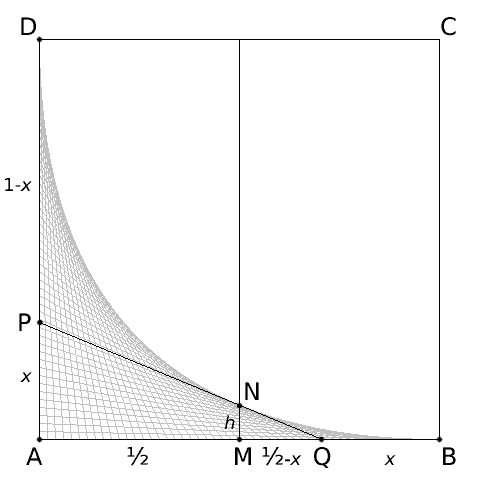
Figura 5.

Siamo nel quadrato ABCD di lato unitario. Consideriamo il generico segmento PQ dove:

PA = x

AQ = 1-x

con 0<x<1/2

Sia inoltre:

M = punto medio di AB

MN perpendicolare ad AB

Vogliamo trovare per quale valore di x il segmento MN=h è massimo. In questo caso, N è un vertice del quadrato interno.

Poiché i triangoli AQP e MQN sono simili, possiamo scrivere la seguente uguaglianza:

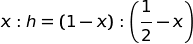
da cui:

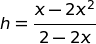
Volendo massimizzare h, calcoliamo la derivata prima e la poniamo uguale a 0.

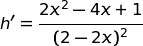
Ponendo il numeratore uguale a 0 abbiamo due soluzioni di cui quella accettabile è:

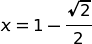
Da cui si ricava, in conclusione:

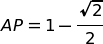
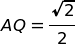
Sostituendo si ottiene:

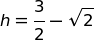
Quindi le coordinate dei vertici del quadrato interno sono:

Come si può scrivere un semplice programma per computer che faccia automaticamente disegni di questo tipo?

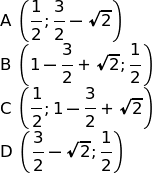
Trascrivo due esempi in DECIMAL BASIC.

Esempio 1.

Il seguente programmino disegna la figura 6.

LET lx=10

LET orig=0

SET WINDOW orig,lx,orig,lx

SET LINE COLOR 27

FOR x=0 TO lx STEP 0.2

 PLOT LINES: 0,(lx-x);x,0

 PLOT LINES: x,0;lx,x

 PLOT LINES: lx,x;lx-x,lx

 PLOT LINES: lx-x,lx;0,lx-x

NEXT x

SET LINE COLOR 4

LET a=lx*0.5

LET b=lx*(3/2-SQR(2))

PLOT LINES: a,b;lx-b,a;a,lx-b;b,a;a,b

END

Figura 6.

Esempio 2.

Il seguente programmino disegna la figura 7, utilizzando la tecnica delle curve di Bezier.

In questo caso sono dati tre punti di controllo: (0;0), (2;10), (10;2).

Poi è tracciata la famiglia di curve di Bezier lineari (rette) che inviluppa la curva quadratica.

LET lx=10

LET orig=-1

SET WINDOW orig,lx,orig,lx

DRAW grid

LET Ax=2

LET Ay=10

LET Bx=0

LET By=0

LET Cx=10

LET Cy=2

FOR t=0 TO 1 STEP 0.02

 LET Pxt=(1-t)*Ax+t*Bx

 LET Pyt=(1-t)*Ay+t*By

 LET Qxt=(1-t)*Bx+t*Cx

 LET Qyt=(1-t)*By+t*Cy

 PLOT LINES: Pxt,Pyt;Qxt,Qyt

NEXT t

END

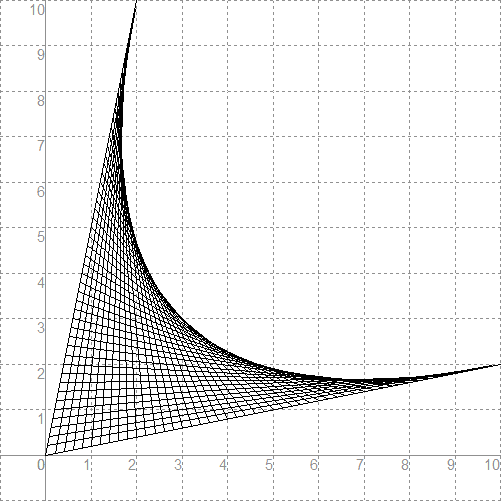
Figura 7.

Pace e bene a tutti!

Gianfranco Bo

Data creazione: settembre 2014

Ultimo aggiornamento: settembre 2014

xhtml 1.1

Sito Web realizzato da Gianfranco Bo