[HOME - BASE Cinque - Appunti di Matematica ricreativa]

Il problema della mitra

ed altre dissezioni

1. Il problema della mitra
Prendete un quadrato e dividetelo in 4 parti tracciando le due diagonali.
Tagliatene via un quarto. La figura che rimane è chiamata mitra perché assomiglia al tipico copricapo indossato dai vescovi nelle funzioni solenni.

E' possibile tagliare la mitra in 5 pezzi e ricomporli in modo da ottenere un quadrato di area uguale a quella della mitra?
Charles Babbage (?)

2. Sam Loyd e il puzzle della mitra
Un giorno qualcuno chiese a Samuel Loyd di dissezionare 3/4 di un quadrato in 4 figure congruenti.
Egli intendeva il tromino-L ma il giovane Sam fraintese e disegnò la mitra.
Disse che impiegò un anno per risolverlo.
Ma questo problema è veramente risolubile?

Il tromino-L è un esempio di gnomon. E' possibile dissezionarlo in 4 parti uguali?

E' possibile sezionare la mitra in 4 figure congruenti?

Questo problema è abbastanza difficile perciò possiamo allenarci con alcuni problemi più facili.

3. Mezza mitra
E' possibile dissezionare mezza mitra in 4 figure uguali?

Loyd, Cyclopedia, 1914

4. Due quadrati in una mitra
Si hanno 2 quadrati. Il lato del secondo è doppio del lato del primo.
Si chiede di dividerli in quattro parti che ricomposte diano una mitra.

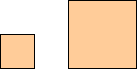
Jackson, Rational Amusement, 1821

5. Sei quadrati per fare una mitra
Si hanno sei quadrati uguali.
E'possibile tagliarne tre e ricomporre i pezzi in modo da formare una mitra?

Jackson, Rational Amusement, 1821

6. Quadrare il rettangolo
E' possibile ritagliare un qualunque rettangolo in un numero finito di pezzi e ricomporli in modo da formare un quadrato che abbia la stessa area del rettangolo?

Risposte & riflessioni

1. Il problema della mitra

2. Sam Loyd e il puzzle della mitra
Soluzione (della prima parte) inviata da Panet

3. Mezza mitra
Soluzioni inviate da Panet e Gea

4. Due quadrati in una mitra

5. Sei quadrati per fare una mitra
Un particolare ringraziamento a Gea per questa soluzione.

6. Quadrare il rettangolo