[BASE Cinque - Appunti di Matematica ricreativa]
Un classico problema generalizzato a n dimensioni.
E' uno dei quesiti più famosi al mondo ma ci sono delle novità.
Per chi si fosse sintonizzato solo ora, riporto il testo del problema nella
sua formulazione di base.
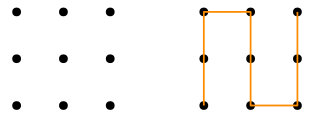
Ci sono 9 punti su un piano disposti in una griglia quadrata 3×3.
Il problema consiste nel disegnare una linea spezzata formata da 4 segmenti che passi attraverso tutti i nove punti.
La linea deve attraversare ogni punto una sola volta.
Qui sotto vedete la griglia 3×3 e a fianco una soluzione errata perché la linea è formata da 5 segmenti invece dei 4 richiesti.

E' uguale al problema di base senza la condizione che la linea passi per ogni punto una sola volta.
In altre parole, la linea può attraversare più volte uno stesso punto.
Questa volta avete 16 punti su un piano disposti in una griglia quadrata 4×4.
Il problema consiste nel disegnare una linea spezzata formata dal minimo numero possibile di segmenti segmenti che passi attraverso tutti i 16 punti.
Qual è tale numero minimo?

Fate altre prove con griglie quadrate di 25, 36, ... punti.
Quali conclusioni potete trarre?
Per risolvere questo problema bisogna pensare fuori dalla scatola (think out of the box).
Ciò significa che non dobbiamo farci condizionare dai confini della griglia. Le linee da tracciare, infatti, devono uscire da questi confini.
Un problema simile a questo fu posto per la prima volta da Samuel Loyd e si trova nella sua Cyclopedia of Puzzles pubblicata nel 1914.
E Samuel Loyd, a sua volta, si ispirò al cosiddetto uovo di Colombo.
Chi sono, allora, gli strani personaggi che compaiono nel disegno?

Figura tratta da Samuel Loyd, Cyclopedia of Puzzles, New York, 1914, pag 301.
Marco Ripà e Pablo Ramirez hanno esteso il problema a una griglia quadrata di N×N punti nel piano e a una griglia cubica di N×N×N punti nello spazio. E sono andati anche oltre: hanno spiegato come sia possibile risolvere questo puzzle negli spazi a più di tre dimensioni.
I risultati delle loro ricerche si trovano nei seguenti articoli:
1) Marco Ripà e Pablo Ramirez, Il Nine Dots Puzzle esteso a N×N×...×N punti.
2) Marco Ripà, Nine Dots Puzzle extended to N1×N2×...×Nk points under house arrest.
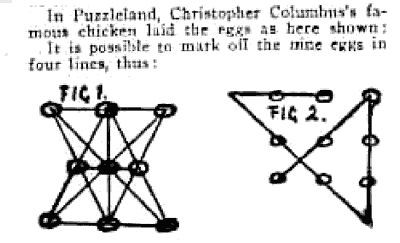
La pagina originale della Cyclopedia of Puzzles dove Samuel Loyd pubblicò il problema.
In rosso è segnato il testo in cui Loyd formula il nostro problema dei 9 punti.

Pagina tratta da Samuel Loyd, Cyclopedia of Puzzles, New York, 1914, pag 301.
Ecco le soluzioni ai due problemi proposte da Loyd.
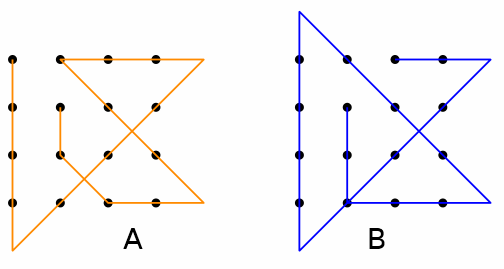
Se ammettiamo che la linea spezzata possa incrociarsi una volta in corrispondenza di uno dei punti della griglia allora il minimo numero di segmenti necessari è 6. (Esempio B)
Se invece stabiliamo che la linea spezzata debba attraversare una sola volta ciascun punto della griglia, allora il minimo numero di segmenti necessari è 7. (Esempio A)
Data creazione: luglio 2013
Ultimo aggiornamento: luglio 2013
xhtml 1.1
Sito Web realizzato da Gianfranco Bo