[HOME - BASE Cinque - Appunti di Matematica ricreativa]
di Utervis
Un ringraziamento particolare a Francesco Veneziano, che ha aperto la strada della soluzione relativamente al caso dei poligoni regolari e soprattutto all'amico Flavio Cimollin, per l'appoggio costante e i suoi notevoli contributi nella stesura della seconda parte di quanto segue.
Se in un rettangolo tracciamo le due diagonali, in modo da collegare tutti i suoi vertici fra loro, si contano cinque nodi, punti di intersezione tra due rette congiungenti i vertici, compresi questi stessi, quattro superfici o regioni, delimitate da un area chiusa e finita, ed otto linee che collegano due nodi qualsiasi.
In un qualsiasi esagono quanti nodi, quante superfici e quante linee riusciamo a contare? Ed invece, in generale, in poligono con n vertici?
N.d.E. Questo problema riprende la Ricreazione n. 264 di Settembre 2002, L'orologio di Utervis alla quale sono state date illuminanti risposte da Enrico Delfini, Sprmnt21, Francesco Veneziano.
Ringrazio Utervis per la seguente esauriente spiegazione. Un lavoro veramente grande!
Lasciamo per un momento da parte il caso dell'esagono, per poi tornarci su successivamente, e trattiamo dapprima il caso generale stabilendo delle regole che valgano per qualsiasi figura poligonale chiusa. Consideriamo quindi che questa sia costituita da n lati ed n vertici: per prima cosa numeriamo da uno ad n tutti i vertici. Il primo di questi lo possiamo collegare ai restanti n - 1, ottenendo così le prime n - 1 linee di confine: di queste, due sono i lati del poligono base e le restanti n - 3 sono le diagonali vere e proprie, congiungenti, cioè, due vertici non consecutivi fra loro. Passando al secondo vertice si nota che anche questo lo possiamo collegare agli altri n - 1, ma dobbiamo escludere il lato 12, già considerato precedentemente, per cui occorre aggiungere n - 2 linee di confine di cui un lato del poligono ed n - 3 diagonali. Passiamo al terzo vertice e, con ragionamento analogo, troviamo che dobbiamo aggiungere altre n - 3 linee di confine. Alla fine possiamo collegare il vertice n - 1 solo con n, ed n con nessuno. Quante linee di confine abbiamo tracciato fin ora? Evidentemente abbiamo:
(n - 1) + (n - 2) + (n - 3) + .... + 2 + 1 + 0
Ora se raggruppiamo gli n termini n abbiamo un primo termine pari a n·n; a questo dobbiamo sottrarre un secondo termine costituito dalla somma dei primi n numeri naturali (lo zero finale è, infatti, pari ad n - n) che sappiamo essere n·(n + 1)/2. Quindi la sommatoria precedente è uguale a:
n·n - n·(n + 1)/2 = n·[n - (n + 1)/2] = n·(2·n - n - 1)/2 = n·(n - 1)/2
Un altro modo per ottenere lo stesso risultato è il seguente: se n sono i lati (e i vertici) del poligono, da ogni angolo parte una congiungente con tutti gli altri vertici, quindi n volte n - 1 congiungenti, per un totale di n·(n - 1) linee, di cui, come detto, due sono lati del poligono e le restanti diagonali. Ogni congiungente unisce due vertici, perciò esse sono conteggiate due volte e numericamente sono solamente n·(n - 1)/2 di cui n lati ed n·(n - 3)/2 diagonali.
Ad esempio per il rettangolo risulta n = 4 e la formula dà come risultato sei. Però questo non è ancora il totale delle linee di confine perché qualcuna di tale congingente si interseca con altre determinando dei nodi interni in più rispetto ai vertici di partenza i quali dividono le diagonali determinate in più parti. Nel rettangolo, infatti, il nodo interno spezzetta le due diagonali in quattro linee di confine a cui si aggiungono i quattro lati della figura. Ed allora quanto occorre aggiungere al risultato ottenuto? Occorre determinare il numero di questi nodi interni ...

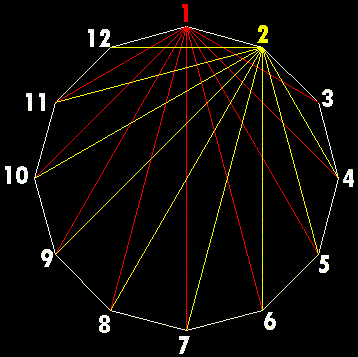
Per poter determinare il numero di questi nodi interni consideriamo il dodecagono regolare raffigurato sopra. Dal vertice 1 abbiamo fatto partire le diagonali rosse (più i due lati che lo uniscono coi vertici adiacenti, 2 e 12) e dal vertice 2 le diagonali gialle (più i due lati che lo uniscono coi vertici 3 ed 1). Come si nota da 1 inizialmente (prima di fare le diagonali gialle) non si intercetta ancora alcun nodo interno; quando però andiamo ad inserire anche le linee gialle la prima di queste, dal vertice 2 al vertice 4, forma già un primo nodo interno, poi, con la seconda diagonale, dal vertice 2 al vertice 5, altri due nodi, poi rispettivamente tre con la terza diagonale, quattro con la quarta diagonale, e così via ... fino all'ultima diagonale, dal vertice 2 al vertice 12, che genera nove nodi interni. Tornando alla generalizzazione dal secondo vertice si determinano complessivamente:
1 + 2 + 3 + ... + n - 3
nodi interni. Questi sono pari alla somma dei primi n - 3 numeri naturali:
(n - 3)·(n - 2)/2
che possiamo vedere anche pari al numero triangolare n - 3.
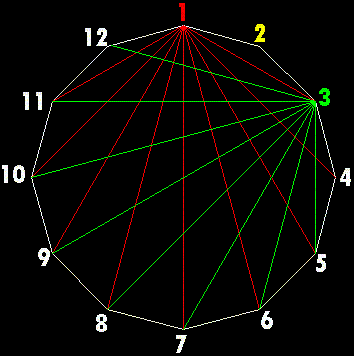
Passiamo al vertice 3 del dodecagono con tutte le diagonali in verde e contiamo dapprima quanti nodi interni si generano con le diagonali rosse: la prima, dal vertice 3 al vertice 5, forma un primo nodo, poi, dal vertice 3 al vertice 6, altri due nodi, poi analogamente altri tre, quattro, e così via fino all'ultima diagonale, dal vertice 3 al vertice 12, che ne genera otto. Non dobbiamo commettere l'errore di considerare anche la diagonale dal vertice 3 al vertice 1 perché essendo colorata in rosso lo abbiamo già fatto dal vertice 1 al 3. Generalizzando dal terzo vertice si determinano:
1 + 2 + 3 + ... + n - 4 = (n - 4)·(n - 3)/2
che possiamo vedere anche pari al numero triangolare n - 4. Contiamo ora quanti nodi interni generano le diagonali verdi uscenti dal vertice 3 con quelle gialle uscenti da 2:
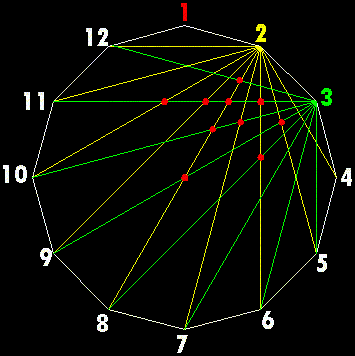
la prima, dal vertice 3 al vertice 5, forma un primo nodo, poi, dal vertice 3 al vertice 6, altri due nodi, poi rispettivamente altri tre, altri quattro, e così via ... fino all'ultima diagonale, dal vertice 3 al vertice 12, che ne genera otto. Come al solito non dobbiamo considerare la diagonale dal vertice 3 al vertice 1 perché essendo rossa lo abbiamo già fatto da 1 a 3. Si hanno così altri (n - 4)·(n - 3)/2 nodi, ma non tutti risultano inediti: in particolare quelli evidenziati nella figura precedente con un puntino rosso erano già stati individuati negli incroci delle diagonali uscenti dal vertice 1 con quelle uscenti dal vertice 2 e non concorrono alla generazione di ulteriori nodi in più, ma, come si vedrà meglio in seguito, solo per valutare diversamente il numero delle linee di confine totali. Nel dodecagono regolare questi nodi in comune per le diagonali partenti dal terzo vertice sono ben dieci come si vede dalla figura. Nei poligoni irregolari può accadere, invece, che si abbiano solo alcune di queste coincidenze o che non si abbiano affatto. Definiamo allora poligono "irregolare nel modo massimo" quello nel quale da ogni vertice qualsiasi diagonale genera sempre nodi interni inediti dando così luogo al numero massimo di tali nodi. Evidentemente nel poligono regolare si ha sempre il numero minimo di nodi interni in quanto si ha un numero maggiori di nodi coincidenti che individueremo meglio in seguito. Andiamo ora a caccia del loro valore massimo che, come detto, si ha nel poligono irregolare nel modo massimo. Come visto dalle formule precedenti quelle che si hanno dal vertice 3 sono in tutto:
[(n - 4)·(n - 3)/2] + [(n - 4)·(n - 3)/2] = (n - 4)·(n - 3)
che possiamo vedere anche pari al doppio del numero triangolare n - 4. Passiamo al vertice 4: ripetendo un ragionamento del tutto analogo a quello fatto per i vertici che lo precedono si vede facilmente che nel poligono irregolare nel modo massimo le diagonali che escono da 4 intercettano (n - 5)·(n - 4)/2 nodi con le diagonali uscenti dal vetrice 1 ed altrettanto se ne intercettano sia con le diagonali uscenti dal vertice 2 che quelle uscenti nel vertice 3 per un totale pari questa volta a:
3·(n - 5)·(n - 4)/2
nodi, che possiamo vedere anche pari al triplo del numero triangolare n - 5. Per un generico nodo i intermedio essi sono:
(i - 1)·(n - i)·(n - i - 1)/2
e per il nodo finale n:
(n - 1)·(n - n)·(n - n - 1)/2 = 0
Vediamo allora per il vertice n - 1:
(n - 2)·(n - n + 1)·(n - n + 1 - 1)/2 = 0
e per quello n - 2:
(n - 3)·(n - n + 2)·(n - n + 2 - 1)/2 = (n - 3)
che possiamo anche vedere anche pari a n - 3 volte il primo numero triangolare che è pari ad 1. Per tutti gli n vertici per poligono irregolare nel modo massimo si hanno in definitiva:
0 + [(n - 3)·(n - 2)/2] + [(n - 4)·(n - 3)] + [3·(n - 5) ·(n - 4)/2] + ... + + [(i - 1)·(n - i)·(n - i - 1)/2] + ... + [(n - 3)·1] + 0 + 0
Questa somma, apparentemente difficile da calcolare, possiamo vederla anche come la somma dei primi n - 3 numeri triangolari più il doppio della somma dei primi n - 4 numeri triangolari più la somma del triplo dei primi n - 5 numeri triangolari e così via di seguito ... fino ad arrivare alla somma degli n - 3 volte il primo numero triangolare. In altri termini essa risulta pari a:
[n·(n - 2)·(n - 1)/6] + [2·n·(n - 3)·(n - 2)/6] + [3·n·(n - 4)·(n - 3)/6] + ... + [(n - 1)·1]
Sviluppando questa somma, dopo vari passaggi, si ottiene, quale risultato finale, che il numero complessivo dei nodi interni di un poligono irregolare nel modo massimo con n vertici vale:
n·(n - 1)·(n - 2)·(n - 3)/24
Un altro modo per ottenere lo stesso risultato è il seguente: se si prendono quattro vertici fra gli n possibili, che chiamiamo con A, B, C e D (contati in ordine uno dietro l'altro), e si tirano le diagonali AC e BD si intuisce chiaramente che si può caratterizzare un solo nodo interno dando una quaterna qualsiasi di vertici, e che una quaterna di vertici identifica uno ed un solo punto di incrocio, dato che gli altri lati, AB, CD, AD e BC, non hanno altri punti di incrocio. Allora il numero di nodi interni non è altro che il numero di differenti quaterne che si possono formare a partire da n punti, ovvero, indicando con ! il simbolo di fattoriale ed utilizzando il coefficiente binomiale, è il numero:
C(n,4) = n!/[4!·(n - 4)!] = n·(n - 1)·(n - 2)·(n - 3)/24
come ricavato sopra.
Ora che conosciamo il numero di nodi interni di un poligono irregolare nel modo massimo possiamo determinare il numero delle linee di confine che scaturiscono da essi. Infatti, poiché dall'intersezione di due diagonali qualsiasi si ha un solo nodo che divide ciascuna di essa in due, le linee di confine aumentano di due per ogni nodo interno indipendentemente se una, o entrambe, le diagonali considerate sono bisecate da un'altra diagonale. L'esempio classico lo si ha col rettangolo: una volta tracciate le sue due diagonali si ha un solo nodo interno e quindi le linee di confine complessive sono le precedenti più altre due. Segue che nel poligono irregolare nel modo massimo di n lati queste saranno pari al doppio dei nodi interni e quindi in definitiva pari a:
n·(n - 1) ·(n - 2) ·(n - 3)/12
che andremo ad aggiungere ai:
n·(n -1)/2
determinati all'inizio, per un totale di linee di confine L pari a:
L = [n·(n - 1)·(n - 2)·(n - 3)/12] + [n·(n - 1)/2] = [n·(n - 1)·(n - 2)·(n - 3) + 6·n·(n - 1)]/12 = = n·(n - 1)·[(n - 2) ·(n - 3) + 6]/12
Il numero complessivo di nodi N è invece pari alla somma di quelli interni e di quelli perimetrali, cioè dei vertici, che sono n, per un totale di:
N = [n·(n - 1)·(n - 2)·(n - 3)/24] + n
Passiamo ora a determinare il numero delle superfici S: consideriamo anzitutto la figura più elementare, cioè un triangolo qualsiasi in cui è evidente che si hanno tre nodi, una superficie e tre linee. A questo punto se a tale triangolo aggiungiamo un secondo triangolo, che abbia in comune con il precedente un lato, si avranno quattro nodi, due superfici e cinque linee, ma, tracciando anche la seconda diagonale, cinque nodi, quattro superfici ed otto linee. Insomma, aggiungendo, di volta in volta, un nuovo triangolo, che abbia sempre in comune un lato con uno dei triangoli precedenti, i nodi e le superfici aumentano di uno, ma le linee di due, per cui sommando il numero dei nodi con il numero delle superfici e sottraendo il numero delle linee il risultato è sempre pari ad uno:
N + S - L = 1
che prende il nome di formula di Eulero, da cui:
S = 1 + L - N
Per un poligono generico di n lati il numero minimo di triangoli da esso ricavabile è pari semplicemente ad n - 2: basta, infatti, considerare che da un qualsiasi vertice partono n - 3 diagonali e che ognuno di essa è in comune ai due triangoli adiacenti.
A questo punto abbiamo tutti gli elementi per determinare le varie quantità per un poligono irregolare nel modo massimo: ad esempio per un esagono si ha:
N = [n·(n - 1)·(n - 2)·(n - 3)/24] + n = [6·(6 - 1)·(6 - 2)·(6 - 3)/24] + 6 = 15 + 6 = 21 L = n·(n - 1)·[(n - 2)·(n - 3) + 6]/12 = 6·(6 - 1)·[(6 - 2) ·(6 - 3) + 6]/12 = 6·5·18/12 = 45 S = 1 + L - N = 1 + 45 - 21 = 25
La cosa si complica notevolmente quando si passa ai poligoni regolari. Infatti, vediamo, solo per curiosità, tutte le diagonali del poligono regolare con un numero di vertici pari a 30:
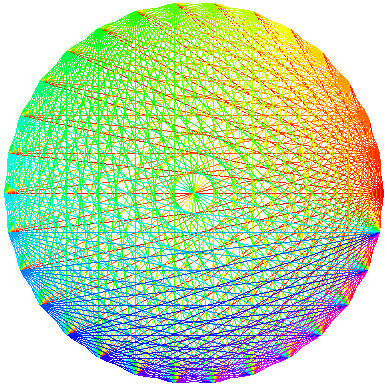
Nel disegno su riprodotto notiamo sì dei nodi interni in comune, ma lo stesso non rende certamente l'idea di quante diagonali in tutto passano per questi. Per poterli ammirare adeguatamente cliccate sulla figura stessa: tale operazione consentirà l'apertura di una nuova finestra esplorativa nella quale, visto il notevole ingrandimento, è possibile valutare davvero quegli stupendi punti in cui si incrociano fin anche sette diagonali, oltre al baricentro dove ne passano addirittura 15.
Pur volendo restare coi piedi per terra diamo anche uno sguardo al nostro dodecagono regolare, che poi non è una figura così eccezionale come la precedente:
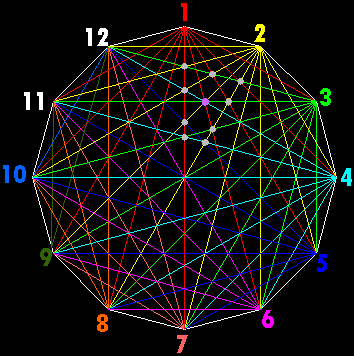
Come si vede nel centro della figura si incontrano addirittura sei diagonali ed è facile intuire che per tutti i poligoni con un numero n pari di lati esattamente n/2 diagonali si incontreranno nel suo centro. Infatti, se n è dispari alcuna diagonale può passare per il centro visto che nessun vertice risulta simmetrico ad un altro rispetto al centro stesso; viceversa per n pari una diagonale per poter passare per il centro deve collegare necessariamente un vertice con quello opposto, dal momento che in tali tipi di figure ogni vertice ne ha solamente un altro di opposto, per cui dopo n/2 vertici tutti quanti sono stati collegati a due a due. Ma, escludendo il centro, cerchiamo di capire quanti sono questi punti che possiamo finalmente definire "multipli". Nel dodecagono notiamo la presenza di svariati punti multipli: in alcuni in cui si incrociano solo tre diagonali, definendo un "nodo doppio", in altri in cui addirittura se ne incrociano quattro generando così un "nodo triplo". In figura sono evidenziati solo quelli in uno spicchio, dato che per simmetria tutti gli altri saranno analoghi: i nodi doppi sono stati colorati in grigio, i tripli in viola. In generale possiamo dire che se m diagonali di un poligono regolare si intersecano nello stesso punto esse generano un nodo (m - 1)-plo (il centro del dodecagono è perciò un punto quintuplo).
Curiosamente, quello che abbiamo visto lo potremmo avere tutti davanti agli occhi ogni giorno: basta prendere un orologio e collegare fra di loro ad esempio le ore 12-5, 1-8, 2-10 e 3-11. Miracolosamente tutte e quattro le linee si incontreranno in un unico punto!

La dimostrazione di questa serie di coincidenze non è particolarmente difficile, ma non è facilmente estendibile al caso generale di determinare il numero di punti di intersezione delle diagonali di un poligono regolare con n lati. Infatti, la successione al variare di n è estremamente irregolare e difficile da studiare. Il primo a risolvere questo intricato problema fu il matematico olandese Gerrit Bol, che ne diede una soluzione completa nel 1936. Peccato che compì una serie di errori nel calcolare alcuni dei coefficienti della formula finale. Nei decenni successivi fu dimostrato dapprima che tre diagonali non si intersecano mai nello stesso punto se il numero di lati n è un numero primo, poi che in generale non si hanno intersezioni multiple se n è dispari ed infine che non si possono intersecare nello stesso punto più di sette diagonali (escludendo sempre il centro dei poligoni con un numero pari di lati) che generano, per quanto detto, al massimo punti sestupli. La soluzione vera e propria del problema è stata individuata solo nel 1995 da B.Poonen e M. Rubinstein, ma il fatto più sconcertante è che è stata trovata grazie all'ausilio indispensabile del computer. Infatti, ci sono stati troppi calcoli per poter essere eseguiti a mano, ed in effetti ci sarebbe stato davvero da stupirsi se nel lontano 1936 Bol fosse riuscito a non commettere neanche un errore. Nel 1995 invece i due matematici sono partiti da una considerazione geometrica che permettesse di far luce su quando tre diagonali si intersecano. Se disponiamo sei punti, A, B, C, D, E, ed F, su una circonferenza e tracciamo i tre segmenti AB, BE e CF come nella figura che segue:

allora si può dimostrare, senza troppa difficoltà, che le tre diagonali si incontrano in un unico punto P se e solo se:
(AF·BC·DE) / (CD·EF·AB) = 1
Rimaneggiando questa formula ed adattandola al problema sono quindi riusciti a trovare un metodo per affrontarlo. Dapprima utilizzando i numeri complessi ed in particolare le radici dell'unità, ed in secondo luogo con l'applicazione massiccia della teoria dei gruppi di Galois, essi hanno dimostrato che la formula finale doveva avere una forma di un certo tipo ben determinato. Questo non volle ancora dire di aver trovato la formula, dato che mancavano ancora tutti i coefficienti, ma era stata trovata la "forma" della formula! E' come dire che una parabola ha equazione:
y = a·x² + b·x + c
Già, ma quali sono a, b e c?
E a questo punto è stato necessario il ricorso all'uso del computer. Infatti così come per una generica parabola i coefficienti a, b e c possono essere individuati se si conoscono almeno tre punti di essa, allo stesso modo anche i coefficienti della formula in questione possono essere univocamente determinati conoscendo i valori che la formula assume in un certo numero di casi. Questo vuol dire, però, nel nostro problema che è necessario contare "manualmente" quanti sono i punti multipli all'interno di poligoni regolari con un numero di lati n fissato. Fossero bastanti tre o quattro casi il lavoro sarebbe stato facile, ma purtroppo i casi da analizzare per la determinazione dei coefficienti della formula dovevano essere almeno 27, e, sfortunatamente nemmeno i primi 27 casi. In particolare è stato necessario calcolare esattamente il numero di punti multipli all'interno del poligono regolare con la bellezza 420 lati. Si capisce a questo punto come l'ausilio di un computer, e anche potente, sia stato indispensabile ... Alla fine, escludendo il centro della figura poligonale, la formula per la determinazione dei soli nodi interni che ne è risultata è la seguente:
C(n,4) + [d2(n)·(-5·n³ + 45·n² - 70·n + 24)/24] - [d4(n)·3·n/2] + + [d6(n)·(-45·n² + 232·n)/6] + d12(n)·42·n + d18(n)·60·n + d24(n)·35·n - d30(n)·38·n + - d42(n)·82·n - d60(n)·330·n - d84(n)·144·n - d90(n)·96·n - d120(n)·144·n - d210(n)·96·n
in cui C(n,4) è il solito coefficiente binomiale, già determinato in precedenza, mentre dm(n) è un coefficiente che vale uno se n è divisibile per m, altrimenti è nullo. A tali nodi interni vanno quindi ancora aggiunti gli n vertici della figura poligonale regolare ed, eventualmente, il centro di essa se n è pari, per cui è:
N = n + A + C(n,4) + [d2(n)·(-5·n³ + 45·n² - 70·n + 24)/24] - [d4(n)·3·n/2] + + [d6(n)·(-45·n² + 232·n)/6] + d12(n)·42·n + d18(n)·60·n + d24(n)·35·n - d30(n)·38·n + - d42(n)·82·n - d60(n)·330·n - d84(n)·144·n - d90(n)·96·n - d120(n)·144·n - d210(n)·96·n
in cui A vale uno per n pari, altrimenti zero. In particolare, indicando con N2 il numero dei nodi doppi, con N3 quello dei nodi tripli, ..., con N6 quello dei nodi sestupli, Poonen e Rubinstein trovarono che:
N2 = n·{[d2(n)·(5·n² - 48·n + 76)/48] - [d4(n)·3/4] + + [d6(n)·(7·n - 38)/6] - d12(n)·8 - d18(n)·20 - d24(n)·16 - d30(n)·19 + + d42(n)·8 + d60(n)·68 + d84(n)·60 + d90(n)·48 + d120(n)·60 + d210(n)·48}
N3 = n·{[d6(n)·(7·n - 42)/12] - [d12(n)·5/2] - d18(n)·4 + d24(n)·3 + + d42(n)·6 + d60(n)·34 - d84(n)·6 - d120(n)·6}
N4 = n·{[d6(n)·(n - 6)/4] - [d12(n)·3/2] - d24(n)·2 + d42(n)·4 + d84(n)·6 + d120(n)·6}
N5 = 4·n·[d30(n) - d60(n)]
N6 = n·[d30(n) + d60(n)·4]
Dal conteggio di questi nodi multipli è escluso, come al solito, il centro dei poligoni con un numero pari di lati per il quale abbiamo già detto che si intersecano n/2 diagonali per cui risulta (n/2 - 1)-plo.
Noti tutti i nodi multipli con un ragionamento analogo a quello fatto per i nodi interni semplici, ottenuti come intersezione di sole due diagonali, è possibile determinare il numero complessivo delle linee di confine che scaturiscono da essi. Infatti, poiché dall'intersezione di tre diagonali qualsiasi nel medesimo punto si ha un solo nodo doppio che divide ciascuna di essa in due, le linee di confine aumentano di tre, cioè una per ogni diagonale, per ognuno di essi indipendentemente se una delle diagonali considerate è bisecata da un'ulteriore diagonale. Segue che in un poligono regolare di n lati i nodi doppi determinano un incremento delle linee di confine pari al triplo di essi; allo stesso modo si vede che ogni nodo triplo fa aumentare le linee di confine del quadruplo del loro numero, e così via per gli altri nodi multipli. In questo modo possiamo ricavarci quante sono in tutto L, ma, sempre Poonen e Rubinstein, hanno determinato il numero delle superfici di un poligono regolare con n vertici che risulta essere:
S = [(n4 - 6·n³ + 23·n² - 42·n + 24)/24] + [d2(n)·(-5·n³ + 42·n² - 40·n - 48)/48] - [d4(n)·3·n/4] + + [d6(n)·(-53·n² + 310·n)/12] + [d12(n)·49·n/2] + d18(n)·32·n + d24(n)·19·n + d30(n)·36·n + - d42(n)·50·n - d60(n)·190·n - d84(n)·78·n - d90(n)·48·n - d120(n)·78·n - d210(n)·48·n
Noti il numero dei nodi complessivi N ed il numero delle superfici S, con la formula di Eulero, su riportata, è possibile, per finire, risalire al numero delle linee di confine L anche per i poligoni regolari.
In particolare per l'esagono regolare risultando non nulli solo d2(6) e d4(6), insieme ad A, si hanno:
N = n + A + C(n,4) + [d2(n)·(-5·n³ + 45·n² - 70·n + 24)/24] - (3·n/2) = = 6 + 1 + {6!/[4!·(6 - 4)!]} + [(-5·6³ + 45·6² - 70·6 + 24)/24] - (3·6/2) = 6 + 1 + 15 + 6 - 9 = 19
S = [(n4 - 6·n³ + 23·n² - 42·n + 24)/24] + [d2(n)·(-5·n³ + 42·n² - 40·n - 48)/48] - [d4(n)·3·n/4] = = [(64 - 6·6³ + 23·6² - 42·6 + 24)/24] + [(-5·6³ + 42·6² - 40·6 - 48)/48] - (3·6/4) = 25 + 3 - 4 = 24
L = N + S - 1 = 19 + 24 - 1 = 42
Riepilogando per un esagono si hanno, come si può facilmente verificare con semplici figure, un numero di nodi che variano da un minimo di 19, per quelli regolari, ad un massimo di 21, per quelli irregolari nel modo massimo; si hanno poi un numero di linee di confine che variano da 42, per quelli regolari, ad un massimo di 45, per quelli irregolari nel modo massimo; infine si hanno un numero di superfici che può essere pari a 24 od a 25 a seconda che si tratti di un esgono regolare od irregolare nel modo massimo. La differenza esigua tra questi valori però non deve lasciar pensare che è sempre così: in fondo l'esagono regolare è la figura più semplice possibile dal momento che la sua regolarità determina la presenza di solamente un nodo doppio all'interno di essa, esattamente nel centro della figura stessa, ed a seconda che questo si formi o meno si hanno i valori su riportati.
Sito Web realizzato da Gianfranco Bo