[BASE Cinque - Appunti di Matematica ricreativa]

Simmetrie con i tetramini asimmetrici

In questo laboratorio di geometria useremo alcuni tetramini per cercare di costruire forme che abbiano uno o due assi di simmetria.

Gli obiettivi didattici principali sono:

1. Vedere simmetrie assiali in situazioni non standard, cioè, per esempio, quando gli assi di simmetria non sono né orizzontali né verticali.
2. Costruire forme simmetriche.
3. Capire quanto è difficile mettere assieme pezzi asimmetrici per costruire una forma simmetrica, anche quando i pezzi sono pochi.

Per i nostri esercizi useremo i due tetramini asimmetrici che si chiamano L ed S e altri tetramini. Sono problemi classici, risolti da tempo, ma rimangono interessanti per chi li affronta per la prima volta.

I nomi dei tetramini

Per intendersi meglio, conviene dare un nome a ciascun tetramino. Ecco i nomi ufficiali.

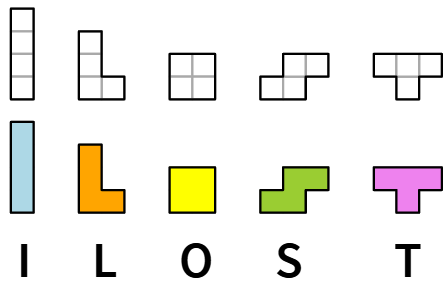
Ci sono 5 tetramini distinti a meno di congruenze, cioè cioè traslazioni, rotazioni e riflessioni (o ribaltamenti) che si chiamano tetramini liberi.

I cinque tetramini liberi

I tetramini L ed S non hanno un asse di simmetria perciò, negli esercizi seguenti, dobbiamo distinguerli dalle loro immagini riflesse (o ribaltate).

Approfondiremo questo aspetto più avanti.

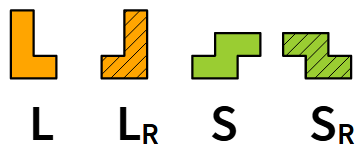
I tetramini L, S e le rispettive immagini riflesse, L_R, S_R

Oddity

---

Definizione. Una polyomino oddity è una figura piana con un asse di simmetria formata da un numero dispari (2n+1) di polimini.

---

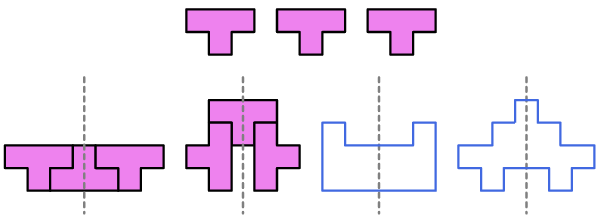
1. Con 3 T. Usando 3 tetramini T è possibile creare una forma con un'asse di simmetria?
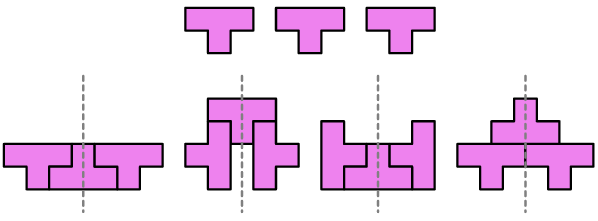
Il tetramino T ha un asse di simmetria. Ci sono molte soluzioni ed è facile trovarle. Ecco alcuni esempi.

2. Con 3 L. Usando 3 tetramini L è possibile creare una forma con un'asse di simmetria?
Se necessario, si può ribaltare un tetramino.
Ci sono 2 soluzioni possibili.

Un piccolo suggerimento.

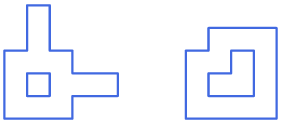
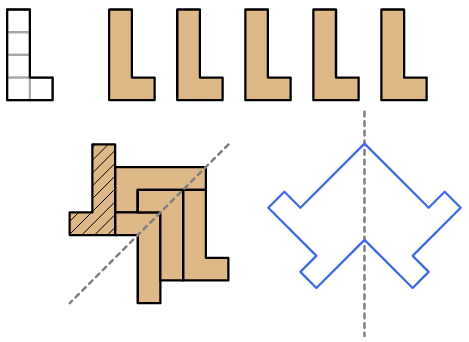
3. Con 5 L. Usando 5 tetramini L è possibile creare una forma con un'asse di simmetria senza buchi?
Se necessario, si può ribaltare un tetramino.

Un piccolo suggerimento.

4. Con 5 pentamini L. Usando 5 pentamini L è possibile creare una forma con un'asse di simmetria?
Se necessario, si può ribaltare un pentamino. Questa costruzione è difficile.

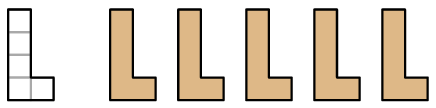
Un piccolo suggerimento.

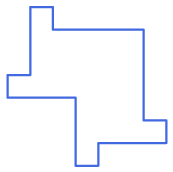
5. Con un numero dispari di S. Usando un numero dispari di tetramini S, è possibile creare una forma con un'asse di simmetria?
Questa costruzione, forse, è impossibile, ma provate comunque a realizzarla.

Semioddity

Negli esercizi precedenti, la oddity n. 5, forse è impossibile da realizzare.
Quando una oddity è impossibile, ci possiamo accontentare di una semioddity.

---

Definizione. Una polyomino semioddity è una figura piana con 2 assi di simmetria, formata da 2(2n+1) polimini.

Osservate che 2(2n+1) è un numero pari non multiplo di quattro.

---

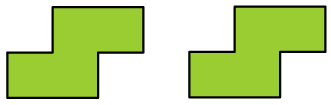
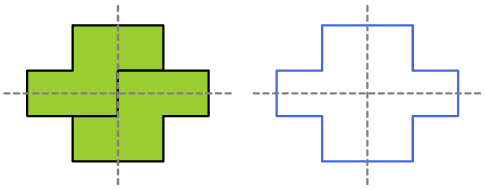
6. Con 2 S. Create una forma con due assi di simmetria usando 2 tetramini S.

7. Con 6 S. Create una forma con due assi di simmetria usando 6 tetramini S.
Se necessario, si possono ribaltare alcuni tetramini. Questa costruzione è difficile.

Un piccolo suggerimento.

Risposte & riflessioni

I nomi dei tetramini

Riprendiamo alcune definizioni.

Cos'è un tetramino?

• Definizione per genere e differenza:
  Un tetramino è un polimino formato da 4 quadrati.

Va bene, ma cos'è un polimino?

• Un polimino è una forma geometrica composta da quadrati uguali uniti fra loro lungo almeno un lato.

Così abbiamo il monomino, il domino, il trimino, il tetramino, il pentamino, e così via. Ecco alcuni esempi.

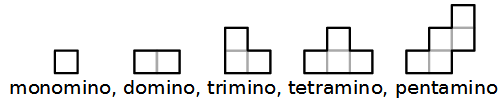
Quanti sono i tetramini liberi?

Provate a disegnare tutte le forme diverse che si possono ottenere usando 4 quadrati uguali uniti fra loro per almeno un lato.

Si ottengono 5 forme che si chiamano tetramini liberi.

Un tetramino libero è un tetramino considerato a meno di congruenze geometriche, cioè traslazioni, rotazioni, riflessioni (o ribaltamenti).

I 5 tetramini liberi

Cos'è la chiralità?

Osserviamo che i tetramini I, O, T rimangono uguali a se stessi quando vengono ribaltati cioè sono sovrapponibili alle loro immagini riflesse.
Invece L, S non sono sovrapponibili alle rispettive forme riflesse. Questa proprietà si chiama chiralità.
Una forma geometrica è chirale se non può essere sovrapposta alla sua immagine riflessa usando solo traslazioni e rotazioni.

I tetramini L ed S sono chirali.

Quanti sono i tetramini unilaterali?

Se escludiamo la possibilità di riflettere (o ribaltare) un tetramino, allora otteniamo 7 tetramini unilaterali distinti. Questi tetramini sono quelli usati nel gioco del Tetris.

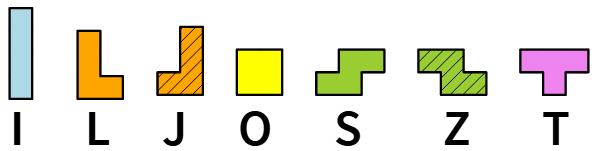
I 7 tetramini unilaterali

Oddity

1. Con 3 T. Usando 3 tetramini T è possibile creare una forma con un'asse di simmetria?

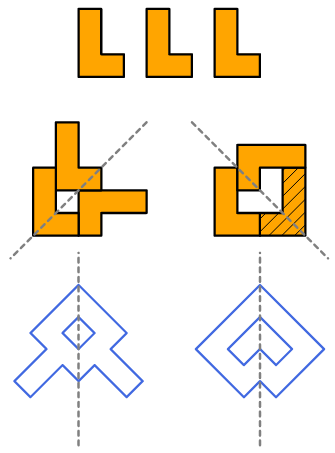
2. Con 3 L. Usando 3 tetramini L è possibile creare una forma con un'asse di simmetria?
Se necessario, si può ribaltare un tetramino.
Ci sono 2 soluzioni possibili.

3. Con 5 L. Usando 5 tetramini L è possibile creare una forma con un'asse di simmetria senza buchi?
Se necessario, si può ribaltare un tetramino.

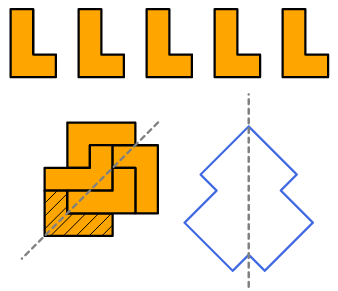
4. Con 5 pentamini L. Usando 5 pentamini L è possibile creare una forma con un'asse di simmetria?
Se necessario, si può ribaltare un pentamino. Questa costruzione è difficile.

5. Con un numero dispari di S.Usando un numero dispari di tetramini S, è possibile creare una forma con un'asse di simmetria?
Questa costruzione, forse, è impossibile, non ho ancora trovato né una soluzione né una dimostrazione di impossibilità.

Semioddity

6. Con 2 S. Create una forma con due assi di simmetria usando 2 tetramini S.

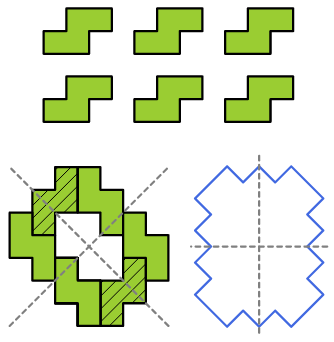
7. Con 6 S. Create una forma con due assi di simmetria usando 6 tetramini S.
Se necessario, si possono ribaltare alcuni tetramini. Questa costruzione è difficile.

---

Pace e bene a tutti.

GfBo

Data creazione: gennaio 2025

Ultimo aggiornamento: gennaio 2025

html5

Sito Web realizzato da Gianfranco Bo