[HOME - BASE Cinque - Appunti di Matematica ricreativa]

Il paradosso della ruota

attribuito ad Aristotele

Il paradosso della ruota è attribuito (con qualche dubbio) ad Aristotele.
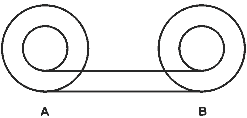
Consideriamo una ruota formata da due cilindri coassiali, di diametro diverso, incollati l'uno sull'altro. In pratica, una ruota formata da due ruote saldate assieme.
Quando la ruota rotola dalla posizione A alla posizione B, le due ruote da cui è formata, come si vede dalla figura, "rotolano" percorrendo esattamente la stessa distanza.
Ed ecco il paradosso: le due ruote devono avere la stessa circonferenza perchè facendo un giro completo percorrono la stessa distanza! Ma è impossibile che due cerchi differenti abbiano la stessa circonferenza!
Come si spiega?

Risposte & riflessioni

L'errore sta nel fatto che in realtà se una delle due ruote rotola allora l'altra striscia.
In altri termini: le circonferenze delle due ruote hanno lo stesso numero di punti (infiniti con cardinalità aleph1) ma ciò non significa che hanno la stessa lunghezza.