[BASE Cinque - Appunti di Matematica ricreativa]

Sei punti a distanze intere fra di loro

Problema 1. Posizionare 6 punti a distanze intere fra di loro

Siete capaci di posizionare 6 punti su un piano in modo che la distanza tra ciascuna coppia di essi sia un numero intero e non ce ne siano tre allineati?

Precisazioni.

1. Per distanza tra due punti si intende la misura del segmento di retta che li congiunge. Si chiama distanza euclidea.
2. Come unità di misura si può fissare una unità arbitraria.
3. Per rendere più semplice e chiara la soluzione, conviene segnare i punti su un piano cartesiano e darne le coordinate. In questo modo è facilissimo verificare la risposta applicando il Teorema di Pitagora.

Problema 2. Posizionare n punti a distanze intere fra di loro

Una generalizzazione: è possibile posizionare in un piano 7, 8, 9, ..., n punti con lo stesso criterio?

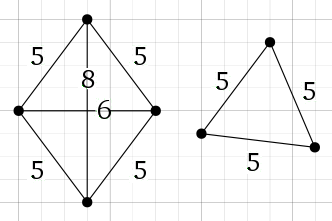
Qui sotto vedete due esempi con 4 e 3 punti.

Risposte & riflessioni

Problema 1. Posizionare 6 punti a distanze intere fra di loro

Una possibile soluzione: il punto segnato con una "x" è l'origine delle coordinate, la figura ha due assi di simmetria e i 6 punti si trovano su una circonferenza.

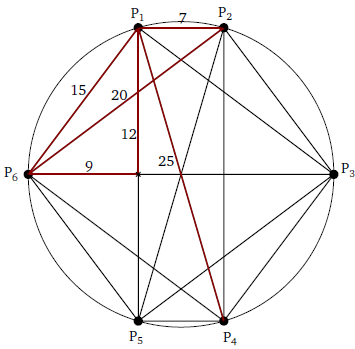
Grazie a Massimo e Alessandro per le seguenti considerazioni.

Se A, B e C sono una terna pitagorica, i 6 punti hanno le seguenti coordinate:

P1:(0;A*B)

P2:(B²-A²;A*B)

P3:(B²;0)

P4:(B²-A²;-A*B)

P5:(0;-A*B)

P6:(-A²;0)

Si ricava infatti facilmente:

Distanza di P1 da P2 uguale a B²-A²

Distanza di P1 da P3 uguale ad B*C

Distanza di P1 da P4 uguale a C²

Distanza di P1 da P5 uguale a 2*A*B

Distanza di P1 da P6 uguale a A*C

Distanza di P2 da P3 uguale ad A*C

Distanza di P2 da P4 uguale a 2*A*B

Distanza di P2 da P5 uguale a C²

Distanza di P2 da P6 uguale a B*C

Distanza di P3 da P4 uguale a A*C

Distanza di P3 da P5 uguale a B*C

Distanza di P3 da P6 uguale a A² + B²

Distanza di P4 da P5 uguale a B²-A²

Distanza di P4 da P6 uguale a B*C

Distanza di P5 da P6 uguale a A*C

Problema 2. Posizionare n punti a distanze intere fra di loro

Paul Erdos e Norman Herbert Anning nel 1945 hanno dimostrato che:

For any n we can find n points in the plane not all on a line such that their distances are all integral, but it is impossible to find infinitely many points with integral distances (not all on a line)

Fonte: NORMAN H. ANNING AND PAUL ERDÖS, INTEGRAL DISTANCES, UNIVERSITY OF MICHIGAN, 1945

Teorema (Erdos-Anning).

Per qualunque n è possibile trovare n punti nel piano, non tutti su una stessa linea retta, tali che le loro reciproche distanze siano tutte numeri interi.

Non è invece possibile trovare infiniti punti nel piano a distanze reciproche intere a meno che non si trovino tutti su una stessa retta.

Il testo dice "non tutti su una stessa retta" ma nella dimostrazione si dà un esempio di come costruire un insieme di n punti, tutti a distanze intere fra di loro, dei quali nessuna terna giaccia sulla stessa retta.

La dimostrazione usa due teoremi:

Teorema 1.

Il quadrato di ogni numero primo p della forma 4k+1 si può esprimere come somma di due quadrati di numeri interi.

p² = a²+b²

Per dimostrare questo teorema, si usano altri due teoremi:

Teorema (di Fermat). Per ogni numero primo p della forma 4k+1, si ha che:

p = a²+b² , con a, b interi.

Teorema. Se due numeri interi sono entrambi somme di due quadrati, allora lo è anche il loro prodotto.

Teorema 2 (Tolomeo).

In ogni quadrilatero inscritto in una circonferenza, la somma dei prodotti delle coppie di lati opposti è uguale al prodotto delle diagonali.

Data creazione: febbraio 2013

Ultimo aggiornamento: marzo 2013

xhtml 1.1

Sito Web realizzato da Gianfranco Bo