La spirale aurea

Un particolare ringraziamento a Ivana per aver proposto il problema al Forum e a Elena per aver dato una risposta mooolto interessante.

Date Posted: 11/06/04 21:48
Author: Ivana
Subject: Spirale esterna...
Desidererei soddisfare una mia curiosità, per cui chiedo se qualcuno conosce il procedimento per la costruzione geometrica della spirale esterna al rettangolo aureo... Potete vedere l'immagine, che ho tratto dal libro "Gnomon" di Paolo Zellini, nella seguente pagina web:

proprio nel punto in cui ho presentato la recensione di tale libro. Si tratta dell'unica immagine non animata, a fianco della seguente scritta: (L'immagine, non animata, del rettangolo aureo è stata tratta dalla pagina 177 del libro "Gnomon" di Paolo Zellini)

L'equazione della spirale aurea
Dopo aver affrontato gli argomenti dal punto di vista qualitativo e geometrico sorgono le domande:
1) Qual è l'equazione della spirale aurea?
2) Che differenza c'é fra la spirale approssimata con il compasso e quella esatta?

Risposte & riflessioni

Prima di affrontare l'immagine di Zellini vediamo come si può ottenere la "spiralizzazione canonica" del rettangolo aureo.
Ho ottenuto i disegni di questa pagina utilizzando il MSW Logo 6.5b di Brian Harvey e George Mills.
Osservate il disegno a destra.

- Si comincia col disegnare un quadrato di lato unitario.

- Si continua disegnando altri quadrati sempre più piccoli disposti a spirale come illustrato nella figura.

- Il lato di ogni quadrato sta nel rapporto aureo con il lato del quadrato che lo segue nella serie.

Il procedimento può continuare all'infinito.

Ricordo che il numero aureo (phi) si ottiene risolvendo la proporzione:
1:x=x:(1-x)
x=(sqr(5)-1)/2=0,6180... è detto la parte aurea dell'unità.
Il rapporto tra l'unità e la sua parte aurea è detto numero aureo ed è solitamente indicato con il simbolo F (phi).

F =

Il reciproco di F (phi) è:

1/F =

Perciò il lato del quadrato (n+1)-esimo si ottiene moltiplicando il lato del quadrato n-esimo per il reciproco del numero aureo.

Da notare che:
(1+phi) : 1 = 1 : phi

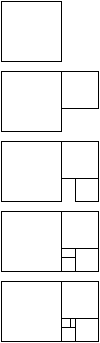Come si vede, la successione di quadrati è interamente contenuta in un rettangolo i cui lati sono proporzionali ai numeri 1 e F (phi). Tale rettangolo è detto rettangolo aureo.
Tale rettangolo così suddiviso può essere chiamato "rettangolo aureo spiralizzato".

NOTA. Con il linguaggio LOGO è comodo costruire la spirale nel modo illustrato. Se invece usiamo carta e matita è più comodo partire dal rettangolo aureo e suddividerlo in due parti: un quadrato e un rettangolo aureo simile al primo. Si ripete la procedura sul secondo rettangolo aureo e così via.

La spirale interna
Man mano che si costruisce la spirale di quadrati si può anche disegnare la spirale (logaritmica?) interna con il compasso.
Si tratta di una approssimazione formata da una sequenza di archi di cerchio.

Si deve puntare il compasso successivamente nei punti indicati dai bollini rossi.
Come si vede i due centri e il punto di raccordo sono sulla stessa linea retta.
Questo accorgimento garantisce che il raccordo sia "buono" cioè che i due archi ammettano la stessa tangente in quel punto.

Le fasi successive della costruzione della spirale interna.
La spirale può proseguire indefinitamente.

L'idea di Elena
E se vogliamo costruire la spirale esterna? Le seguenti figure illustrano l'idea di Elena.

La spiegazione data da Elena
Per cercare di capire come si potesse disegnare "l'approssimazione" della spirale "esterna" (e dando per scontato che la suddivisione del rettangolo aureo dovesse essere la "solita"), ho cercato la posizione dei centri degli archi di circonferenza (esterni ai lati lunghi dei rettangoli).

Posto il rettangolo di lati 1 e

nel primo quadrante di un riferimento cartesiano ortogonale, con il vertice A nell'origine, il centro dell'arco DC ha ascissa

, ma ordinata da determinare.

Ho determinato queste incognite (in realtà l'incognita si riduce ad una sola sfruttando la similitudine dei due rettangoli aurei) imponendo che le due circonferenze siano "ben raccordate" nel punto C (cioè in C ammettano la stessa retta tangente).

Quindi gli archi approssimanti la spirale esterna erano ancora quarti di cerchio. E' da qui che ho pensato alla coincidenza con la spirale interna di un altro rettangolo aureo, e precisamente di quello (nel disegno in rosso) di lato minore pari a

e ruotato di 45° rispetto al primo (in nero).

Un po' di Logo
Il Logo è un linguaggio geniale.
Con poche semplici procedure è possibile ottenere risultati straordinari.
Ecco le pricipali procedure che ho scritto per realizzare i disegni di questa pagina.
Ho utilizzato il MSW Logo 6.5b di Brian Harvey e George Mills che può essere scaricato gratuitamente dalla rete.

1) Questa disegna un quadrato di lato l (elle)
to qua :l
repeat 4 [fd :l rt 90]
end

2) Questa costruisce una spirale di quadrati i cui lati si rimpiccioliscono di un fattore phi (num. aureo). Si parte da un quadrato di lato l (elle) e si procede per n passi.
to spiqua2 :l :n
repeat :n [qua :l pu fd :l rt 90 fd :l pd make "l :l*0.618]
end

3) Questa costruisce due spirali di quadrati, una nera e una rossa disposte opportunamente.
to dspiqua :l :n
spiqua2 :l :n
pu home fd :l pd rt 45 make "l :l*(1+sqrt(5))/(2*sqrt(2))
setpencolor [255 0 0]
spiqua2 :l :n
setpencolor [0 0 0]
end

Dal punto di vista matematico la dimostrazione "visiva", in questo caso, non ci dà alcuna certezza.
Bisognerebbe dimostrare che la spirale dell'equazione passa per TUTTI i punti di tangenza dei quadrati via via più piccoli.
Coraggio!

Dov'é l'origine della spirale?
Disegniamo un rettangolo di base F (phi) e di altezza 1 con il vertice A nell'origine delle coordinate cartesiane.
Facciamo la costruzione canonica della spirale aurea.
Dov'é l'origine della spirale, ovvero il centro del vortice logaritmico?
La figura qui sotto può aiutare a trovare la soluzione. All'interno di ogni quadrato è riportata la misura del suo lato.

Ox = 1 + 1/F⁴ + 1/F⁸ + 1/F¹² + ... = ?
Oy = 1 - (1/F + 1/F⁵ + 1/F⁹ + ...) = ?

Ringrazio Elena per la seguente risposta.
Direi che Ox e Oy si determinano bene.

Infatti Ox è la somma di una serie geometrica di ragione 1/(phi)^4 = (7-3sqr5)/2 <1, e quindi coverge a
1/(1-(1/phi^4)).
Oy risulta esattamente 1- (1/phi)Ox.

Si può estendere il concetto alla spirale interna ad ogni rettangolo aureo di lato minore l (elle), posizionato allo stesso modo nello stesso riferimento.
La spirale converge a:

Ma torniamo al rettangolo aureo di lato minore 1.
La spirale esterna allora converge a:

, anche se rispetto ad un riferimento ruotato di 45° e centrato in D (D,x,h).