[BASE Cinque - Appunti di Matematica ricreativa]
E' possibile
ritagliare da un foglio di carta una qualsiasi forma poligonale con un unico
taglio rettilineo.
Ma prima bisogna piegare opportunamente il foglio stesso.
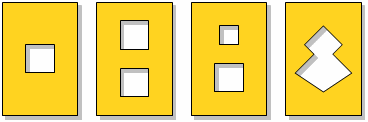
Chi è capace di ritagliare un foro quadrato in un foglio di carta con un unico taglio rettilineo fatto con le forbici?
E due fori quadrati? E una qualunque forma poligonale?
La soluzione è sempre possibile ma prima di fare il taglio bisogna piegare opportunamente la carta.

Riporto le soluzioni attraverso immagini con brevi commenti.
Da parte vostra, c'è bisogno di osservare con attenzione, ragionarci su e fare qualche prova per capirle bene.

E' un classico:
Quindi si taglia via la punta come illustrato in figura.
Il taglio è unico e rettilineo, ma aprendo il foglio si ottiene un foro quadrato.

Questo metodo è più elegante, preciso e utile del primo.
Osservate la fotografia.
Le pieghe sono le stesse della soluzione 1, ma le "montagne" e le "valli" (diedri convessi e concavi) rispetto a chi guarda il foglio sono diversi.
Anche il taglio è diverso.

E' il doppio della soluzione 2.
Si piega il foglio a metà parallelamente al lato più corto.
In ciascuna delle due metà, indipendentemente dall'altra, si opera come nel caso 2.
Dopo si sovrappongono le due metà piegate in modo da farle coincidere.

Un altro punto di vista del caso 3.

Le pieghe del foglio dal lato prevalentemente concavo.

Le pieghe del foglio dal lato prevalentemente convesso.

L'obiettivo è ottenere una situazione simile a quella dei due fori uguali, ma con le due punte da ritagliare leggermente sfasate.

Si piega il foglio parallelamente al lato più corto NON a metà, in modo da ottenere due parti rettangolari leggermente diverse.
In ciascuna delle due parti si fanno le piege come nel caso dei due fori quadrati uguali.
Naturalmente, in una parte le misure delle pieghe saranno più piccole che nell'altra.
Ora viene il difficile.

Bisogna procedere quasi come nel caso dei due fori quadrati uguali.
La piega a punta fatta nella parte più piccola deve però essere più in basso (o in alto) dell'altra.
La foto sopra illustra un momento critico della piegatura.

Dopo aver appiattito bene il foglio piegato, si tagliano le due punte con un unico taglio.
ATTENZIONE: nella foto qui sopra sembra che si siano fatti due tagli, ma è una specie di illusione ottica. La causa è che il foglio non è benschiacciato, ma la parte superiore si è notevolmente alzata rispetto a quella inferiore.

Ecco il risultato finale.


Erik Demaine ha studiato il problema del taglio unico (fold and cut problem) e ha pubblicato i risultati delle sue ricerche in diversi articoli e nel suo sito: http://erikdemaine.org/folding/.
In particolare, ha dimostrato il teorema che suona più o meno così:
Teorema
Qualunque collezione di segmenti di retta può essere ottenuta mediante un unico taglio dopo aver opportunamente piegato un foglio rettangolare.
Erik D. Demaine (nato il 28 febbraio 1981, a Halifax, Nova Scotia, Canada), è professore di Computer Science presso il MIT (Massachusetts Institute of Technology).
Data creazione: giugno 2011
Ultimo aggiornamento: giugno 2011
xhtml 1.1
Sito Web realizzato da Gianfranco Bo