[BASE Cinque - Appunti di Matematica ricreativa]

La spirale di Teodoro di Cirene

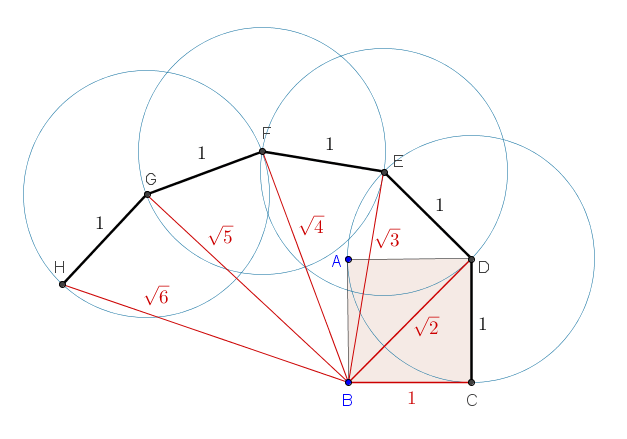
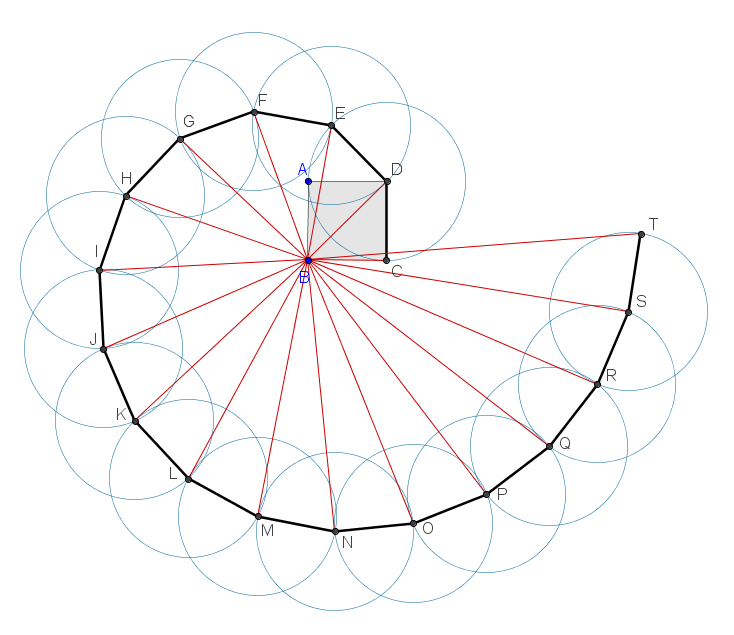
Un metodo grafico per costruire le radici quadrate di tutti i numeri interi

Come si costruisce

I disegni geometrici di questa pagina sono eseguiti con Geogebra.

1. Si parte dal quadrato ABCD di lato unitario.
2. Si traccia la diagonale del quadrati che è lunga √2
3. Si traccia il segmento ED = 1 perpendicolare alla diagonale BD.
   EB = √(2+1) = √3
4. Si traccia il lato FE = 1 perprendicolare a BE.
   FB = √(3+1) = √4 = 2
5. E così via...

Furbo questo Teodoro, vero?

Andando avanti...

Le misure degli angoli

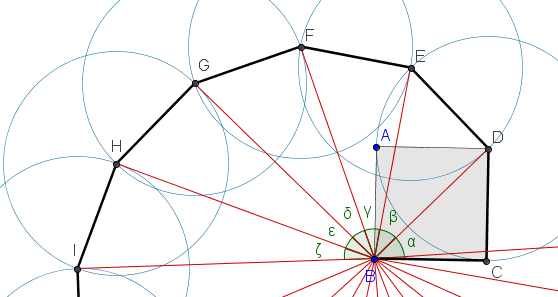
α = 45°

β = 35,26...°

γ = 30°

δ = 26,57...°

ε = 24,09...°

ζ = 22,21...°

... da approfondire

Nota storica

Attenti a non confondere!

Con il nome Teodoro di Cirene vengono indicati:

• Teodoro di Cirene (morto nel 310) - vescovo e santo martire, celebrato il 4 luglio
• Teodoro di Cirene (IV-III secolo a.C.) - detto "l'ateo", esponente della Scuola cirenaica
• Teodoro di Cirene (V secolo a.C.) - matematico della Scuola pitagorica

Il nostro Teodoro è stato un matematico greco antico. Noto per i suoi contributi alla teoria delle grandezze irrazionali, fece parte della Scuola pitagorica.

Sappiamo dal Teeteto, dialogo di Platone, che Teodoro insegnò matematica allo stesso Platone e a Teeteto. Infatti nel dialogo si ricorda come avesse dimostrato che le radici dei numeri compresi fra √3 e di √17 (scongiuro!), esclusi ovviamente 9 e 16, fossero irrazionali, cioè non esprimibili come rapporto di interi. Sappiamo anche che introdusse un metodo per costruire geometricamente la radice quadrata di un qualsiaisi numero esistente, anche se non molto utilizzato per motivi pratici: la cosiddetta spirale di Teodoro.

(Tratto, con alcune correzioni da Wikipedia)

Data creazione: luglio 2012

Ultimo aggiornamento: luglio 2012

xhtml 1.1

Sito Web realizzato da Gianfranco Bo