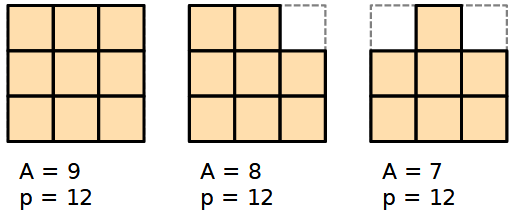
[BASE Cinque - Appunti di Matematica ricreativa]
Quanti quadrati al massimo puoi togliere da una griglia quadrata senza far cambiare la misura del suo perimetro?
La famiglia di problemi che vi propongo in questo articolo ha a che fare con un concetto importante di geometria piana: l'area è una misura additiva. Anche il perimetro è una misura additiva ma si comporta in modo diverso da quello dell'area. Per esempio, se uniamo due quadrati lungo un lato, le loro aree si sommano mentre il perimetro della loro unione NON è uguale alla somma dei loro perimetri.
I problemi proposti possono aiutare a comprendere meglio questo aspetto e a non commettere errori banali quando si usa l'additività delle misure.
Approfondiremo l'argomento dopo gli esercizi.
Una griglia 3x3 di quadrati di lato 1 ha area A = 9 e perimetro p = 12.
Si può togliere un quadrato in modo da ottenere una figura di area 8 e perimetro ancora uguale a 12.
Si può togliere un altro quadrato in modo che l'area sia 7 e il perimetro sempre 12.
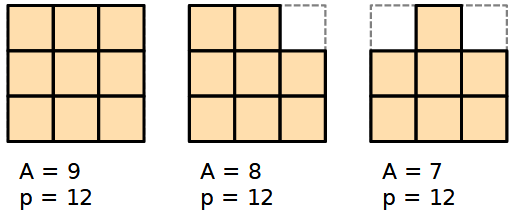
Quanti e quali quadrati si possono togliere al massimo per ottenere una figura che abbia il perimetro uguale a 12 e area minima?
---
Precisazione. I quadrati che formano le figure devono avere almeno un lato in comune. Per esempio, la figura qui sotto non è una soluzione accettabile.
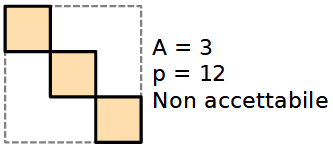
---
20 esagoni di lato unitario formano una griglia esagonale di perimetro 30.
Si possono togliere, per esempio, due esagoni in modo da ottenere una figura di perimetro 34.
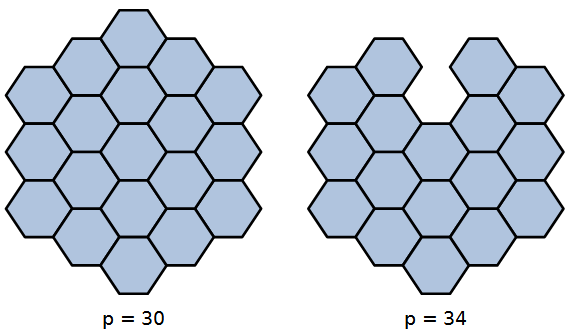
Quanti e quali esagoni si devono togliere affinché il perimetro della
figura ottenuta sia il più grande possibile?
Questa griglia di 25 triangoli equilateri di lato unitario ha il perimetro uguale a 15.
Si può togliere un triangolo in modo da far aumentare il perimetro.
Continua a togliere triangoli, uno alla volta in modo da far aumentare il perimetro della figura.
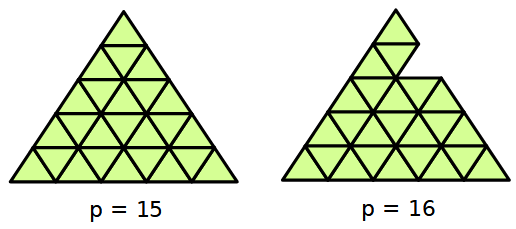
Quanti e quali triangoli puoi togliere al massimo con questo criterio e quanto misura il perimetro della figura ottenuta?
---
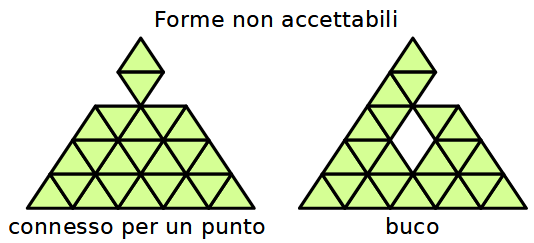
Precisazione. Le figure ottenute devono essere poligoni semplici, cioè niente buchi né intrecci.
Per esempio, le figura qui sotto non sono accettabili.
Consideriamo un quadrato di lato 5 unità.
La sua area è 25 unità2.
Il suo perimetro è 20 unità.
(d'ora in avanti ometterò le unità di misura)
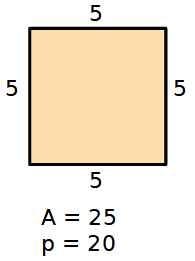
Immaginiamo di unire 2 di questi quadrati lungo un lato.
Quanto misurano l'area e il perimetro del rettangolo ottenuto?
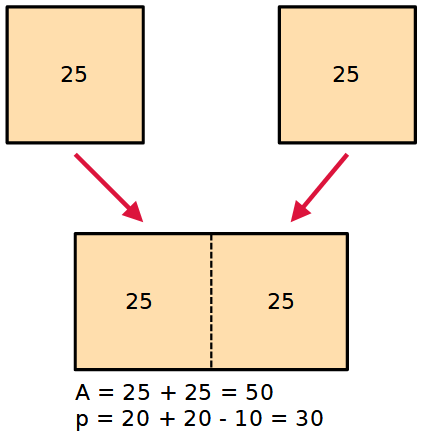
In questo caso:
Questa proprietà vale quando i due quadrati (o altri poligoni) sono uniti lungo uno o più lati o parte di essi.
La proprietà non vale quando i poligoni hanno superfici in comune.
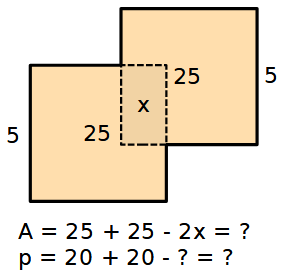
Quando i due quadrati (o altri poligoni) sono uniti solo per un punto, sia l'area, sia il perimetro sono additivi.
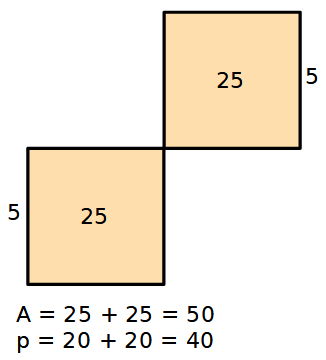
Ancora un piccolo pro-memoria molto semplice.
Consideriamo due poligoni P e Q non sovrapposti.
Nella figura seguente sono uniti fra loro soltanto lungo una parte del perimetro di ciascuno. Ricordiamo che l'area di un segmento è uguale a 0.
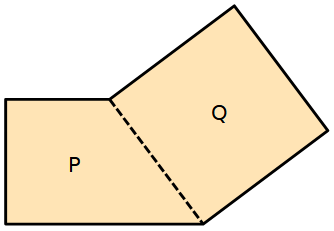
La loro unione forma un nuovo poligono che chiamiamo P ∪ Q
Indichiamo con area(X) la funzione area che associa al poligono X un numero reale non negativo che rappresenta la misura della sua superficie.
Abbiamo che:
area(P ∪ Q) = area(P) + area(Q)
---
In generale, una misura m è additiva quando:
Dati due insiemi disgiunti, la misura della loro unione è uguale alla somma delle misure dei due insiemi.
Se P ∩ Q = ∅
allora
m(P ∪ Q) = m(P) + m(Q)
Riporto alcune soluzioni, ma potrebbero esisterne altre.
---
1) Perimetro costante
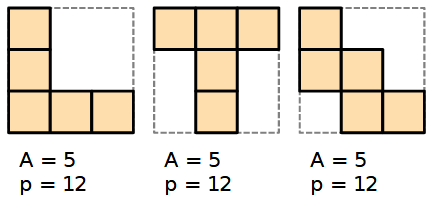
---
2) Perimetro massimo
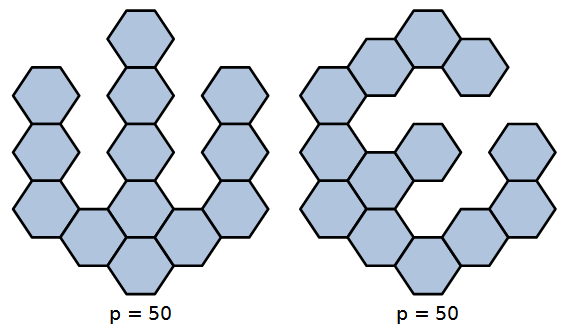
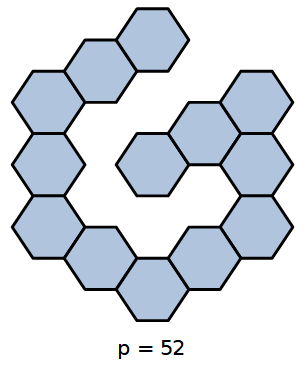
---
3) togli triangoli
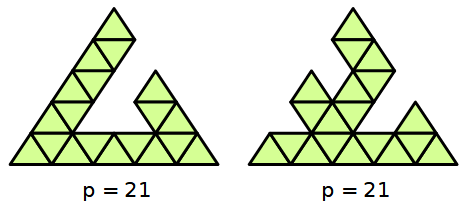
---
Pace e bene a tutti.
GfBo
Data creazione: settembre 2023
Ultimo aggiornamento: ottobre 2023
html5
Sito Web realizzato da Gianfranco Bo