[BASE Cinque - Appunti di Matematica ricreativa]
Un puzzle per dimostrare la formula del volume della piramide.
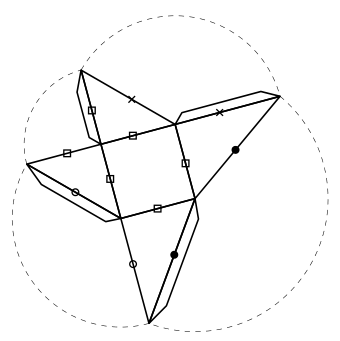
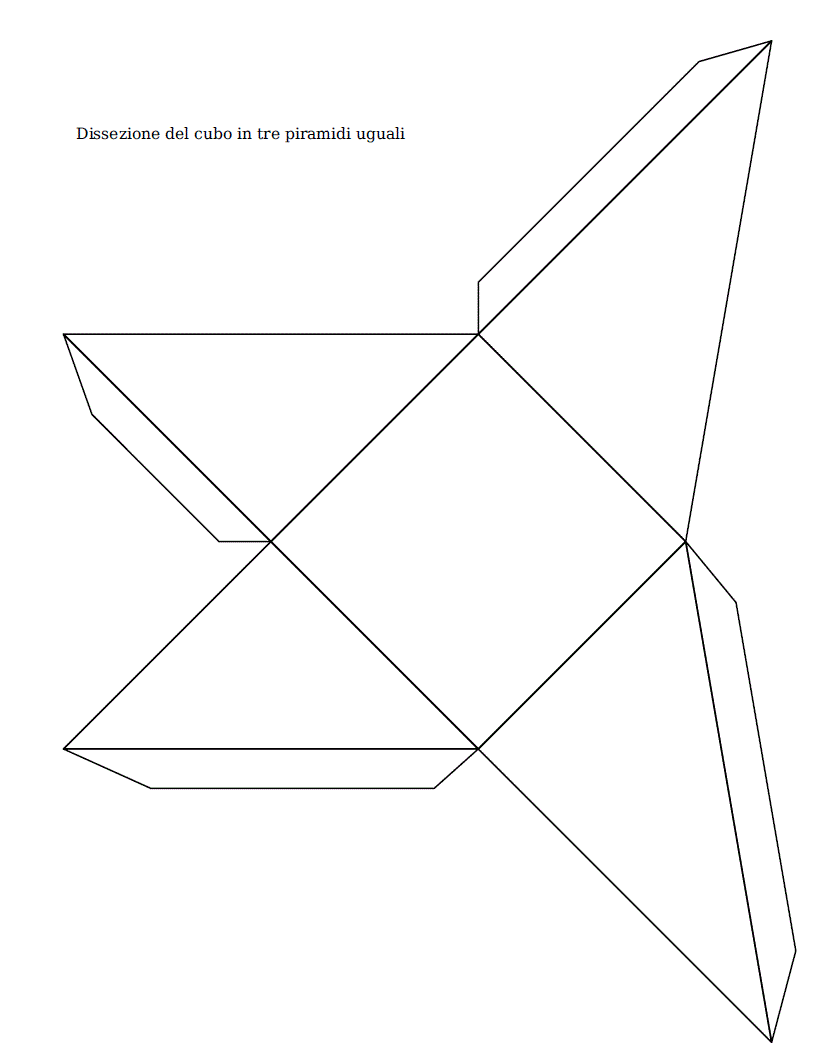
Costruite almeno 4 piramidi uguali di cartoncino che abbiano uno sviluppo sul piano come questo (in fondo alla pagina c'è un'immagine stampabile più grande e precisa):

A segni uguali corrispondono segmenti uguali.
Ciascuna piramide ha le seguenti caratteristiche:
Orbene, con tre di queste piramidi si può assemblare un cubo che ha le facce uguali alla base delle piramidi. E naturalmente l'altezza uguale all'altezza delle piramidi.

Le nostre piramidi sotto vari punti di vista.

Con 4 piramidi si può fare una piramide più grande quadrangolare regolare.

Con 3 piramidi si possono fare i 3/4 della piramide grande...

...oppure un cubo.

Ecco il cubo finito.
Così si dimostra la formula del volume della piramide: area di base per altezza diviso tre.
Con la classe 3C del 2012, abbiamo deciso di costruire una scatola cubica per le tre piramidi.
Lo spigolo della scatola deve essere circa 3 mm più grande del cubo formato dalle piramidi.
Ecco la nostra scatola vuota con accanto le tre piramidi.

Entra la prima piramide...

Entra la seconda piramide...

Entra la terza piramide...

Abbiamo anche il coperchio!

Le tre piramidi montate fuori della scatola.

Data creazione: febbraio 2011
Ultimo aggiornamento: maggio 2012
xhtml 1.1
Sito Web realizzato da Gianfranco Bo