[BASE Cinque - Appunti di Matematica ricreativa]

Il problema di Tammes

... e le sfere di bicchieri

Procuratevi una pinzatrice e 100 bicchierini di plastica, di quelli piccoli, da caffé.

Facoltatico uno spray argentato o dorato.

Prima prova: bicchieri sul piano

Prendete 1 + 6 + 12 + 18 + 24 + ... biccheri.

Figura

Posate un bicchiere in mezzo alla tavola.

Mettetegli intorno altri 6 bicchieri. Ci stanno perfettamente.

Figura Figura

Aggiungete, intorno alla struttura altri 12 bicchieri e poi altri 18 e poi...

Figura Figura

Potete andare avanti all'infinito.

Seconda prova: bicchieri nello spazio

In questa prova dovete unire i bicchieri con due punti di pinzatrice, uno vicino al fondo e uno vicino al bordo.

Figura

Come nella prova precedente, partite da un bicchiere e attaccategliene altri 6 tutto intorno.

Poiché i bicchieri sono conici e non cilindrici, le loro basi non stanno su un piano ma tendono a disporsi su una superficie curva tridimensionale.

Figura Figura

Attaccate allo stesso modo altri 12 bicchieri e poi altri 18.

I bicchieri tendono a formare una sfera ma ben presto ci si accorge che non si possono più disporre in modo regolare, come nella prima prova. Inevitabilmente si devono lasciare spazi vuoti irregolari fra i bicchieri.

Figura Figura

Alla fine, se non forziamo troppo le attaccature fra un bicchiere e l'altro, si forma proprio una sfera.

Possiamo trasformarla in un lampadario o in una decorazione natalizia.

Ci sono voluti 96 bicchieri per fare la sfera che vedete qui sotto.

Figura

A che cosa assomiglia la sfera di bicchieri?

A me ricorda...

L'occhio composto degli insetti?

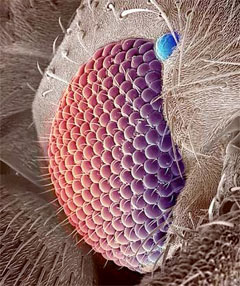
Figura

Occhio composto di moscerino

(Raija Peura, University of Oulu Institute of Electron Optics)

Le diatomee?

Figura

Aulonia hexagona

(http://www.microscopy-uk.org.uk)

I granuli di certi pollini?

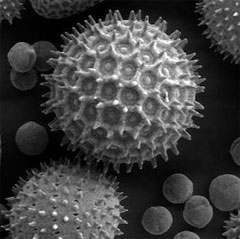
Figura

Pollini

(http://en.wikipedia.org/wiki/Pollen)

Il problema di Tammes

Il problema di Tammes prende il nome dal botanico olandese Pieter Merkus Lambertus Tammes (1903-1980) che pose la questione nel 1930 in relazione allo studio dei pori sui granelli sferici di polline.

Il problema di Tammes si può formulare nel modo seguente

Come ricoprire, senza sovrapposizioni, la superficie di una sfera con n cerchi uguali in modo tale che il loro diametro d_n sia il più grande possibile?
Come si devono sistemare questi cerchi in modo da raggiungere il massimo richiesto?
La soluzione, per ogni n, è unica?

Ecco alcune soluzioni.

I diametri sono espressi come angoli solidi sottesi al centro della sfera.

numero di cerchi n	diametro *d_n*	posizione dei centri dei cerchi
2	180°	estremi di un diametro della sfera
3	120°	vertici di un triangolo equilatero su una circonferenza massima (piano equatoriale)
4	109° 28'	vertici del tetraedro regolare
5	90°	5 dei 6 vertici dell'ottaedro regolare (configurazione non unica)
6	90°	vertici dell'ottaedro regolare
7	77° 52'	configurazione unica
8	74° 52'	antiprisma quadrato
9	70° 32'	configurazione unica
10	66° 9'	configurazione unica
11	63° 26'	11 dei 12 vertici dell'icosaedro
12	63° 26'	vertici dell'icosaedro
24	43° 41'	cubottaedro camuso (o snub cube)

Ecco una soluzione per n=150 (non si sa se è quella ottima)

(http://www.buddenbooks.com/jb/images/150a5.gif)

Figura

Note.

La versione originale del problema di Tammes si trova in: Pieter Merkus Lambertus Tammes, On the origin of number and arrangement of the places of exit on the surface of pollen-grains , Amsterdam, J. H. de Bussy, 1930.

Data creazione: dicembre 2011

Ultimo aggiornamento: dicembre 2011

xhtml 1.1

Sito Web realizzato da Gianfranco Bo