[BASE Cinque - Appunti di Matematica ricreativa]

Il volume del cono

Un semplice esperimento per ricavare una formula matematica

Premessa

Per capire questo esperimento bisogna:

• conoscere la formula per calcolare il volume del cilindro;
• conoscere le basi del calcolo letterale.

Un esperimento con due recipienti

Prendiamo due recipienti a forma di cono e di cilindro.

Il cono e il cilindro hanno lo stesso diametro e la stessa altezza.

Abbiamo bisogno anche di acqua a sufficienza.

Chiediamoci: quanti coni d'acqua servono per riempire il cilindro?

Forse 2? Forse 3?

Proviamo.

Riempiamo il cono d'acqua.

Versiamo l'acqua del cono nel cilindro: 1° volta.

Osserviamo: è sicuramente meno della metà.

Misurando con un righello l'altezza dell'acqua possiamo ipotizzare che è 1/3 dell'altezza del cilindro.

Riempiamo nuovamente il cono d'acqua e versiamola nel cilindro: 2° volta.

Riempiamo nuovamente il cono d'acqua e versiamola nel cilindro: 3° volta.

Il cilindro è pieno. Perfettamente.

Concludiamo che il volume di un cono è 1/3 del volume del cilindro che ha la stessa base e la stessa altezza del cono.

Come possiamo ricavare la formula del volume del cono?

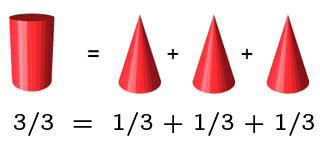
Semplice:

1. prendiamo la formula del cilindro e la dividiamo per 3;

Così calcoleremo il volume di un cono avente lo stesso raggio e la stessa altezza del cilindro.

Orrore! Questa è una formula matematica ricavata empiricamente!

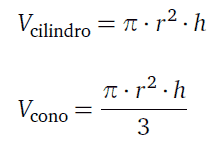
E allora?

Come credete che facesse Archimede?

E i matematici di oggi?

Meraviglia!

Data creazione: giugno 2010

Ultimo aggiornamento: giugno 2010

xhtml 1.1

Sito Web realizzato da Gianfranco Bo