[BASE Cinque - Appunti di Matematica ricreativa]
Come usare un po' di furbizia e di matematica per risolvere un solitario combinatorio
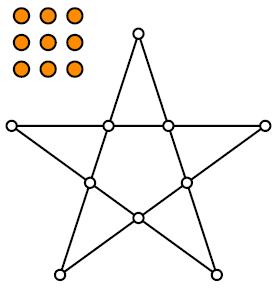
Partendo da un pentagono, si disegna uno schema di stella a 5 punte con 10 caselle vuote: 5 nei vertici e 5 nelle intersezioni delle diagonali.
Si hanno inoltre 9 pedine.

Bisogna mettere le 9 pedine in 9 delle 10 caselle vuote.
Alla fine, una qualunque casella rimarrà vuota.
Qui sotto c'è un esempio.
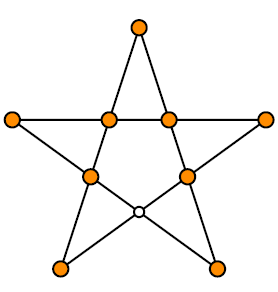
C'è una sola regola.
Per sistemare una pedina, bisogna:
a) partire da una casella vuota indicandola con un dito e dire: "Uno.";
b) segnare altre due caselle poste su uno stesso segmento dicendo: "Due, tre.";
c) la casella di arrivo, la terza, deve essere vuota;
d) posare la pedina sulla terza casella.
Le seguenti figure mostrano uno dei tanti possibili inizi del gioco.
1° pedina
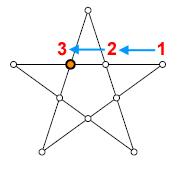
2° pedina
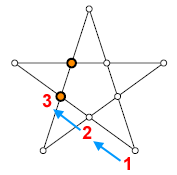
3° pedina
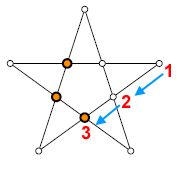
4° pedina
Questo esempio chiarisce che soltanto la prima e la terza casella devono essere vuote. La casella centrale può essere occupata da una pedina.
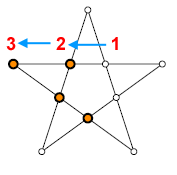
Esiste una strategia automatica per completare lo schema?
Una risposta che ci toglie dagli impicci è: parto da uno schema risolto e procedo a ritroso, una mossa dopo l'altra.
Quindi dovrò togliere nove pedine anziché metterle
Per ogni pedina che tolgo scrivo vicino alla sua casella un numero, contando in senso inverso da 9 a 1.
Alla fine avrò lo schema vuoto con le caselle numerate da 1 a 9. La numerazione rappresenta una possibile soluzione del gioco.
Ecco un esempio.
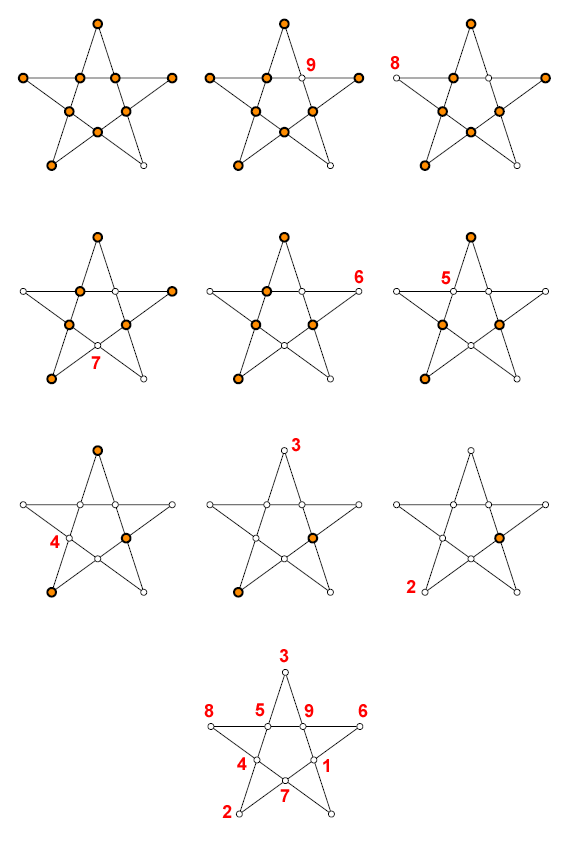
Ma... osservando bene tutto daccapo... anzi, provando a farlo... magari cambiando qualcosa...
si può trovare una strategia generale del tutto automatica e facile da ricordare.
Questa strategia è sempre la stessa, da qualunque punto si parta.
.
.
.
.
.
.
Spiegazione esoterica.
Parto da una casella a piacere C1, conto 1, 2, 3 in una direzione a piacere e metto la prima pedina.
La seconda pedina la metto nella casella C1, partendo con la conta da una casella C2.
La terza pedina la metto nella casella C2, partendo con la conta da una casella C3.
La quarta pedina la metto nella casella C3, partendo con la conta da una casella C4.
E così via.
Con questa strategia c'è sempre una casella vuota da cui partire e una vuota su cui arrivare.
Come si spiega?
...
Ringrazio di cuore Endi Dhima che mi ha insegnato questo gioco.
Data creazione: luglio 2010
Ultimo aggiornamento: luglio 2010
xhtml 1.1
Sito Web realizzato da Gianfranco Bo