[HOME - BASE Cinque - Appunti di Matematica ricreativa]
I quesiti più
conosciuti nel mondo
(al momento siamo a quota 34)
Anche se a scuola non vi hanno mai fatto giocare con la
Matematica ricreativa (e forse non vi hanno neppure detto che esiste) dovreste
senz'altro conoscere almeno tre o quattro dei quesiti seguenti.
Si tratta di una piccola collezione dei classici più conosciuti al mondo.
Provate a risolverli per mettere alla prova la vostra abilità di base ma non
poneteli mai a nessuno per dimostrargli che siete esperti: probabilmente il
vostro interlocutore vi dirà:
- Questo lo conosco benissimo!
N.B. I problemi di questa sezione provengono dalle
fonti più disparate: libri, e-mail, newsgroups, pagine web, confidenze di
amici, etc.
Molti di questi problemi si trovano anche in altre sezioni di Base
Cinque.
1. Il figliol prodigo
Un giovanotto ha ricevuto 1024 Euro in regalo. Ogni giorno spende metà di
quello che possiede.
Dopo quanti giorni rimarrà senza neanche un Euro?
2. L'Euro mancante
Tre amici vanno a cena in un ristorante. Mangiano le stesse portate e il conto
è, in tutto, 25 Euro. Ciascuno di essi paga con un biglietto da 10 Euro, per un
totale di 30 Euro. Quando il cameriere gli porta il resto di 5 Euro, si tengono
1 Euro a testa e gli lasciano 2 Euro di mancia.
Più tardi fanno i conti e dicono: "Abbiamo pagato 9 Euro a testa cioè 9 x 3 =
27 Euro i quali, con i 2 Euro di mancia, fanno 29 Euro. Dov'è finito l'Euro
mancante?"
3. Tutti hanno pagato ma alla fine la cassa è vuota
Tre signori molto onesti ed educati cenano in una locanda. Il primo di loro,
quando ha finito di cenare, chiede il conto. Il padrone gli risponde:
"Vai alla cassa, conta quanti soldi ci sono, mettici altrettanto e prendi come
resto 2 Euro."
Anche il secondo, quando ha finito di cenare, chiede il conto. Il padrone gli
risponde:
"Vai alla cassa, conta quanti soldi ci sono, mettici altrettanto e prendi come
resto 2 Euro"
Il terzo infine, quando chiede il conto riceve la stessa risposta:
"Vai alla cassa, conta quanti soldi ci sono, mettici altrettanto e prendi come
resto 2 Euro."
Quando i tre se ne sono andati il padrone, tutto soddisfatto, apre la cassa e
la trova vuota!
"Il mondo è pieno di ladri! pensa, ma ha torto."
Tenendo conto che i tre signori non hanno rubato nulla ed hanno eseguito alla
lettera le disposizioni del padrone, sapresti dire quanto c'era nella cassa
all'inizio?
4. Il quadrato magico
Sei capace di collocare in una tabella di 3 x 3 caselle i numeri dall'1 al
9 in modo ciascuna riga, ciascuna colonna e ciascuna diagonale dia come somma
15?
| ... | ... | ... |
| ... | ... | ... |
| ... | ... | ... |
5. L'età delle figlie
Un intervistatore bussa alla porta di una casa dove è atteso da una signora. La
signora gli apre e lui chiede:
"Quanti figli ha?"
"Ho tre figlie." gli risponde la donna."
"Età?"
"Il prodotto delle età è 36 e la somma è uguale al numero civico di questa
casa."
"Buon giorno e grazie."
L'intervistatore se ne va, ma dopo un po' ritorna e le dice:
"I dati che mi ha fornito non sono sufficienti."
La signora ci pensa un po' e replica:
"E' vero, che sbadata! La figlia maggiore ha gli occhi azzurri."
Con questo dato l'intervistatore può conoscere l'età delle tre figlie.
Quanti anni hanno?
6. Il tagliatore di corde
Si ha una corda lunga 7 m ed ogni giorno se ne taglia un metro. Dopo quanti
giorni la corda sarà completamente tagliata?
7. La lumaca
Una lumaca si arrampica lungo la parete di un pozzo umido, buio e profondo 5 m.
Ogni giorno sale di 3 m ed ogni notte, mentre dorme, scivola verso il basso di
2 m. Dopo quanti giorni la lumaca potrà uscire dal pozzo?
8. Le dodici monete
Hai 12 monete apparentemente uguali. Però una di esse è falsa e si può
riconoscere perché ha un peso leggermente inferiore alle altre. E' possibile
individuare la moneta falsa effettuando al massimo tre pesate con una bilancia
a bracci uguali?
Nota: una versione più difficile di questo problema è discussa qui: Il famoso problema delle 12 monete.
9. Il problema delle 8 monete (grazie a Giovanni Antonio Chirilli)
Siano date otto monete di cui una falsa e di peso inferiore alle altre. Utilizzando non piu' di due pesate con una bilancia a bracci uguali, si determini qual è la moneta falsa.
Nota: mentre il precedente problema delle 12 monete può essere risolto in più modi, questo problema ha una unica soluzione.
10. Le tre case e le tre fonti
In uno spiazzo ci sono tre case e tre fonti: una d'acqua, una di
elettricità e una di gas. E' possibile collegare ciascuna casa con ciascuna
fonte per mezzo di linee che stiano sullo stesso piano e non si incrocino?

11. I 9 punti e le 4 linee
Tracciare una linea spezzata formata da 4 segmenti che passi per tutti i
punti della figura qui sotto.
Un testo alternativo è il seguente: i punti che vedete in
figura sono disposti lungo una griglia ortogonale, cioè gli otto punti più
esterni giacciono sul perimetro di un quadrato, mentre il restante al centro
del quadrato stesso. Il problema consiste nel coprire questi nove punti con
quattro segmenti di retta senza mai staccare la penna dal foglio.

12. Il prigioniero
Un prigioniero è chiuso in una cella con due porte: una conduce alla
salvezza e l'altra alla morte.
Ciascuna delle due porte è vigilata da un guardiano. Entrambi i guardiani sanno
dove conduce ciascuna delle due porte.
Il prigioniero sa che uno dei due guardiani mente sempre e l'altro dice sempre
la verità ma non sa quale dei due è quello sincero.
Il prigioniero può fare una sola domanda ad uno solo dei due guardiani per
scegliere la porta dalla quale uscirà.
Che cosa deve chiedere se vuole salvarsi?
13. C'è chi mente e chi dice la verità
In una certa città gli uomini sposati mentono sempre e gli scapoli dicono
sempre la verità.
Un giorno una turista vede tre uomini e chiede al primo: "Lei è scapolo o
sposato?"
L'uomo si toglie il sigaro di bocca e risponde: "Io sono cof..cof... po
fkkjsdf8r... cof..."
"Che cosa ha detto il suo amico?" chiede al secondo.
Il secondo sputa il chewing gum e risponde: "Ha detto che è scapolo."
Il terzo uomo si toglie gli occhiali da sole e replica: "Qui l'unico scapolo
sono io!"
Che cosa è ciascuno dei tre uomini?
14. Di che colore è l'orso
Ngongo è molto preoccupato, perché si è perso in una landa sconosciuta.
Percorre 1 km verso sud, poi 1 km verso est, poi 1 km verso nord. Alla fine si
rende conto di trovarsi nel punto esatto da cui era partito.
Mentre sta riflettendo sulla singolare circostanza ode un rumore alle sue
spalle. Si volta di scatto e vede un orso imponente, che prima non aveva
notato.
Di che colore è l'orso?
15. L'uomo nell'ascensore
Un signore abita al decimo piano di un palazzo.
Tutti i giorni, quando esce di casa, prende l'ascensore al decimo piano e
scende fino al pianterreno.
Quando invece rientra in casa, sale con l'ascensore dal pianterreno fino al
settimo piano e sale il resto delle scale a piedi per raggiungere il suo
appartamento.
Quel signore non è superstizioso, non è uno sportivo e odia salire le scale a
piedi. Come mai allora si comporta cosi?
A onor del vero bisogna precisare che quando in ascensore ci sono altre persone
e talvolta quando piove egli arriva con l'ascensore fino al decimo piano.
16. Il lupo, la capra e il cavolo
Un pastore deve attraversare un fiume portando sull'altra riva un lupo e
una capra affamati e un cavolo gigante.
Ha a disposizione una barca a remi con la quale può traghettare un solo oggetto
o animale alla volta.
Ma, attenzione! Non può lasciare da soli:
- il lupo e la capra perché il lupo si mangia la capra;
- la capra ed il cavolo perché la capra si mangia il cavolo.
Quanti viaggi deve fare per portare sull'altra riva il lupo, la capra ed il
cavolo?
17. Un nome davvero singolare: Carlo
Sapresti dire un nome di uomo che non abbia alcuna lettera in comune con il
nome Carlo?
18. Cin Cin
In una tavolata di dieci persone quanti cin cin vengono fatti se ognuno lo fa
con ciascun altro?
19. Una gallina e mezza
Se una gallina e mezzo fa un uovo e mezzo in un giorno e mezzo, quante uova
farà una gallina in sei giorni?
20. L'asino e il mulo
Un asino disse a un mulo: "Se prendessi 20 Kg del tuo carico, il peso che mi
opprime diventerebbe il doppio del tuo".
Il mulo rispose: "Se io prendessi 20 Kg del tuo peso, io porterei un carico
uguale al tuo".
Quale peso portava ciascun animale?
21. Zampe e teste
In una stalla vi sono oche e coniglietti. Contando le teste queste sono 32, le
zampe sono 100. Quante sono le oche e quanti i conigli?
22. Dieci sacchetti da 10 monete
Ho dieci sacchetti contenenti ciascuno dieci monete; in uno di questi sono
contenute monete di peso 0.1 g ciascuna, nei rimanenti nove sono contenute
monete di 1 g ciascuna.
Come posso individuare con una bilancia ad un solo piatto, con una sola pesata
e senza l'aiuto di altri fattori in quale sacchetto sono contenute le monete
che pesano di meno?
23. Attraversare il ponte
Aldo, Bruno, Carlo e Dino devono attraversare un ponte. Purtroppo sono al buio
e possono disporre di una sola torcia (il ponte può essere attraversato solo
con la torcia). Inoltre solo due persone alla volta possono camminare sul
ponte.
Considerando che i 4 impiegano rispettivamente 1, 2, 5 e 10 minuti per
attraversare il ponte e che quando due lo attraversano insieme camminano alla
velocità del più lento (cioè se Aldo, 1 minuto, e Dino, 10 minuti, attraversano
insieme impiegano 10 minuti, altrimenti uno dei due rimarrebbe al buio), come
fanno i nostri 4 amici ad attraversare il ponte in 17 minuti?
24. Quattro triangoli con sei bastoncini
Hai 6 bastoncini della stessa lunghezza, li puoi collegare solo attaccando le
punte. Come fai a formare con essi 4 triangoli?
25. Le 27 palline
Ho 27 palline di cui 26 sono di Ferro e 1 è di Piombo. Come faccio a
determinare quella di Piombo mediante 3 pesate con bilancia a due piatti?
26. I 3 interruttori
Gino e' fuori da una stanza che ha una sola porta (chiusa) e nessuna finestra.
Fuori ci sono tre interruttori. Ognuno può assumere due posizioni etichettate
ON e OFF. Sai che uno di questi accende, quando e' su ON, e spegne, quando e'
su OFF, una lampadina all'interno della stanza. Gino può modificare a
piacimento le posizioni degli interruttori che inizialmente sono tutti su OFF.
Quando vuole può aprire la porta ed entrare nella stanza, però a questo punto
non può più uscire dalla stanza.
Come può fare Gino a capire quale interruttore pilota la lampadina?
27. Con 7 bastoncini
Hai 7 bastoncini cosi posizionati: \/II = I.
Questi descrivono un'equazione sbagliata, spostando un solo bastoncino devi
ottenere un'equazione corretta.
28. Un numero di 5 cifre
Devi trovare un numero di cinque cifre che ha questa proprietà: se gli aggiungi
a destra un 1 diventa tre volte più grande che se gli metti l'1 davanti.
29. Il problema di Monthy Hall
Siamo in un gioco a premi, abbiamo davanti a noi tre porte: dietro una di
queste c'è un'auto, nelle altre due... una capra. Dobbiamo scegliere una porta,
e vinceremo quello che troviamo là dietro. Fatta la scelta, il presentatore ci
dice "Ne sei proprio sicuro? Puoi ancora cambiare la scelta: anzi, ti voglio
aiutare e riduco le scelte a due. Ecco: dietro questa porta, c'è una capra".
Così dicendo, apre una delle porte che noi non abbiamo scelto, mostrando una
capra. Ammesso che vogliamo vincere l'auto, ci conviene cambiare porta, o la
cosa è indifferente?
NOTA: per essere sicuri che il gioco sia compreso correttamente:
- il presentatore ci fa la domanda qualunque sia stata la nostra scelta.
- il presentatore apre sempre una porta diversa da quella scelta da noi,
e la sceglie in modo che abbia dietro una capra
30. Parola d'ordine
Una spia cerca di capire la regola che associa parola e controparola d'ordine
per l'ingresso in un centro segreto. Si nasconde dietro a un cespuglio ed
osserva. Arriva un soldato, bussa al portone e da dentro una voce dice "12", il
soldato risponde "6" e gli viene aperto. Poco dopo arriva un altro soldato,
bussa e gli viene detto "8", lui risponde "4" ed entra. Un terzo soldato entra,
dopo avere risposto "5" alla parola "10". A questo punto, la spia crede di aver
capito tutto: si avvicina, bussa, le dicono "4", lui risponde "2" e gli
sparano. Come mai? (Ovviamente esistono infinite risposte possibili: a me
interessa quella che si esprime con meno parole).
31. I lupi mannari
Una piccola città, in qualche sperduto luogo della terra, è infestata dai lupi
mannari, cioè ci sono alcune persone che durante le notti di luna piena si
trasformano in lupi feroci. Si può quindi ragionevolmente pensare che almeno
uno degli abitanti di questo strano luogo sia un lupo mannaro. Per fare fronte
a questa situazione il sindaco della cittadina emette un'ordinanza, la quale
prevede che ogni cittadino che sappia di essere un lupo mannaro, si debba
uccidere appena lo scopre. Dato che gli abitanti del luogo sono tutti dei
cittadini rispettosi delle leggi, si può dare per certo che effettivamente ogni
abitante che scopra di essere un lupo mannaro si uccida. Purtroppo però, un
lupo mannaro non si accorge di esserlo e quindi lo può solo capire
dall'osservazione di quello che gli sta intorno. A questo punto occorre
ricordare che tutte le notti, e quindi in particolare quelle di plenilunio,
ogni cittadino incontra tutti gli altri, e pertanto è in grado di vedere i lupi
mannari anche se non può comunicare con loro. Dopo la terza notte di luna piena
vengono ritrovati i cadaveri di alcuni lupi mannari. Voi dovete scoprire quanti
sono i lupi ritrovati e soprattutto perché sono stati ritrovati soltanto dopo
la terza notte, mentre nelle due precedenti non si è avuto alcun
ritrovamento.
32. Un filo intorno alla Terra
Supponiamo la terra perfettamente sferica di circonferenza 40000 km, e un filo
della stessa lunghezza che le giri tutto attorno all'Equatore. Tagliamo il
filo, aggiungiamogliene un metro, riannodiamo il tutto e lasciamo il nuovo
anello a distanza costante dalla superficie. Può un gatto passare tra il filo e
la terra?
33. Travasi
Hai tre recipienti, A, B, C che possono contenere al massimo, quando sono
pieni:
Non sono graduati, perciò non è possibile sapere esattamente quanta acqua
contengono, se non quando sono pieni.
All'inizio il recipiente da 8 dl è pieno d'acqua mentre gli altri sono
vuoti.
Devi riuscire ad ottenere esattamente 4 dl d'acqua in uno dei recipienti B o
C.
Puoi travasare dell'acqua da un recipiente ad un'altro quante volte vuoi.
Come fai?
34. Mozziconi di sigaretta
Un barbone raccoglie mozziconi di sigaretta e mettendone assieme 4 si
costruisce una sigaretta (quasi) nuova. Se riesce a fumare 7 sigarette (quasi)
nuove, qual è il numero minimo di mozziconi che deve aver trovato e quanti
gliene rimangono alla fine?
Vi sarete certamente accorti che i top-ten della lista precedente
sono più di 10. La collezione dei classici è infatti numerosissima e molti di
essi sono più antichi di quanto si pensi.
I quadrati magici, ad esempio, erano noti già agli antichi cinesi. Il quesito
del lupo, della capra e del cavolo risale ai tempi del frate Alcuino di York
(900) che scrisse tra l'altro un libro di giochi logici e matematici intitolato
"Ad acuendos juvenes".
In questa piccola collezione sono presenti i campi più significativi della
matematica: l'aritmetica, la geometria, la logica, le strategie combinatorie, i
sistemi di misura, il pensiero laterale.
Data creazione: luglio 2000
Ultimo aggiornamento: aprile 2010
1. Il figliol prodigo
Ringrazio
Giorgio Dendi che mi ha suggerito una correzione al testo di
questo problema.
1° giorno: 1024 Euro.
2° giorno: 512 Euro.
3° giorno: 256 Euro.
...
10° giorno: 2 Euro.
11° giorno: 1° Euro.
12° giorno: 50 centesimi di Euro.
Al 12° giorno rimane con 50 centesimi, cioè senza neanche un Euro.
2. L'Euro mancante
Il ragionamento corretto è questo:
25 Euro per la cena +
3 Euro presi come resto +
2 Euro di mancia al cameriere =
-------------------------
30 Euro.
Va bene, il ragionamento giusto è quello, ma dov'é l'errore nel testo del problema?
Ringrazio Alessandro che mi scrive:
L'errore sta semplicemente nella frase:
"Abbiamo pagato 9 Euro a testa cioè 9 x 3 = 27 Euro i quali, con i 2 Euro di
mancia, fanno 29 Euro. Dov'è finito l'Euro mancante?".
Precisamente ciò che non è corretto è il fatto che si considera due volte la
mancia.
"Abbiamo pagato 9 euro a testa" = OK
"i quali, con i 2 Euro di mancia, fanno 29 Euro" = ERRATO: la mancia era già
compresa nei 27 Euro (25 per la cena e 2 per la mancia).
Addizionare nuovamente la mancia è l'ERRORE.
La frase giusta sarebbe: ""Abbiamo pagato 9 Euro a testa cioè 9 x 3 = 27 Euro i quali, con i 3 Euro di resto, fanno 30 Euro.
3. Tutti hanno pagato ma alla fine la cassa è vuota
All'inizio nella cassa c'erano 1,75 Euro.
Questo problema si risolve partendo dal fondo.
Alla fine nella cassa ci sono: 0 Euro.
Quindi il 3° cliente deve aver trovato 1 Euro. Ha aggiunto altrettanto,
cioè 1 Euro, e si è preso 2 Euro di resto.
Quindi il 2° cliente, per lasciare 1 Euro deve aver trovato 1,5 Euro. Ha
aggiunto altrettanto (1,5 x 2 = 3) e si è preso 2 Euro di resto.
Quindi il 1° cliente per lasciare 1,5 Euro deve aver trovato 1,75 Euro.
Ha aggiunto altrettanto (1,75 x 2 = 3,5) e si è preso 2 Euro di resto.
Quindi nella cassa, all'inizio, c'erano 1,75 Euro.
Facciamo la verifica:
Cassa: 1,75 Euro
1° cliente: (1,75 x 2) - 2 = 1,5
2° cliente: (1,5 x 2) - 2 = 1
3° cliente: (1 x 2) - 2 = 0
Ringrazio Francesco Marra per la seguente soluzione rapida.
Se x è il valore iniziale della nostra cassa allora la cassa:
L'ultima viene imposta a zero... (ma così la possiamo imporre come vogliamo...) e viene magicamente 14/8 = 1,75 euro.
4. Il quadrato magico
Ecco una possibile soluzione.
| 2 | 7 | 6 |
| 9 | 5 | 1 |
| 4 | 3 | 8 |
Grazie a Miky che mi ha inviato un quadrato magico, di dimensioni 4x4.
| 1 | 15 | 14 | 4 |
| 8 | 10 | 11 | 5 |
| 12 | 6 | 7 | 9 |
| 13 | 3 | 2 | 16 |
5. L'età delle figlie
Le figlie hanno rispettivamente 2, 2, 9 anni.
Vediamo di capire perché.
Noi non conosciamo il numero civico della casa, quindi dobbiamo trovare ed
esaminare tutti i casi possibili.
Visto che il prodotto è 36, le età potrebbero essere:
| Possibili terne di età | prodotto | somma | ||
| 1 | 1 | 36 | 36 | 38 |
| 1 | 2 | 18 | 36 | 21 |
| 1 | 3 | 12 | 36 | 16 |
| 1 | 4 | 9 | 36 | 14 |
| 1 | 6 | 6 | 36 | 13 |
| 2 | 2 | 9 | 36 | 13 |
| 3 | 3 | 4 | 36 | 10 |
| 6 | 3 | 2 | 36 | 11 |
Se, ad esempio, il numero civico della casa fosse 14, non ci sarebbero
problemi. L'unica terna di numeri interi che da come prodotto 36 e come somma
14 è 1, 4, 9.
Come si vede dalla tabella, l'unica somma che dà origine ad ambiguità è 13,
alla quale corrispondono due diverse terne, ciascuna delle quali prevede che
due figlie sono gemelle.
Ma la mamma ha precisato: "E' vero, che sbadata! La figlia maggiore ha gli
occhi azzurri."
Da ciò si capisce che la maggiore non ha una gemella, ma è unica.
Quindi possiamo dedurre che le tre figlie hanno 2, 2 e 9 anni.
6. Il tagliatore di corde
Sei giorni, cioè sei tagli. Provare per credere.
7. La lumaca
Al terzo giorno è fuori dal pozzo.
8. Le dodici monete
Divido le 12 monete in 2 gruppi da 6. Chiamiamoli A e B.
1° pesata: confronto i due gruppi A e B. La moneta si trova in quello più
leggero.
Divido le 6 monete in due gruppi da 3 monete ciascuna. Chiamiamoli A1 e B1.
2° pesata: confronto i due gruppi A1 e B1. La moneta si trova in quello più
leggero.
Chiamo le tre monete M1, M2 e M3.
3° pesata: confronto M1 e M2:
a) se hanno lo stesso peso allora la moneta falsa è M3;
b) se hanno peso diverso, la moneta falsa è quella più leggera.
Grazie ad lkc per avermi inviato questa soluzione
alternativa.
E' forse possibile una soluzione differente rispetto a quella
riportata:
1. si dividono le monete in 3 gruppi da 4 (A, B, C) e se ne pesano 2 (diciamo A
e B). se sono = la moneta leggera e' nel gruppo C, altrimenti la moneta falsa
e' nel gruppo piu' leggero dei 2 pesati.
2. si prende il gruppo selezionato e se ne pesano solo 2 monete. Se hanno lo
stesso peso la moneta falsa si trova tra le 2 rimaste (si passa dunque alla
terza pesata), se invece le due monete hanno peso differente, non c'e' bisogno
di passare alla successiva pesata.
Grazie a Giovanni Antonio Chirilli per la seguente
soluzione alternativa.
Ho costatato che nell'indovinello delle dodici monete ci sono, se
non ricordo male, 2 soluzioni. Faccio osservare che ci sarebbe una terza
soluzione (non ho provato a controllare se le soluzioni possibili sono soltanto
3).
Si divide il gruppo di 12 monete in 2 gruppi.
Chiamo i 2 gruppi A e B. A composto da 2 monete e B da 10.
A questo punto considero il gruppo B e pongo 5 monete su ogni piatto. Se il
peso e' uguale allora con la seconda pesata trovo la moneta leggera.
Se sono diverse considero il gruppo di monete che pesa di meno e ne considero
4. Pongo 2 di queste 4 in un piatto e 2 in un altro. Se il peso e' uguale la
restante e' la moneta in questione.
Altrimenti considero le due monete che sono piu' leggere delle altre 2 e con la
terza ed ultima pesata ho finito la ricerca.
9. Il problema delle 8 monete.
Grazie a Giovanni Antonio Chirilli per il problema e la soluzione.
Un quesito un po' piu complicato a mio avviso e quello di considerarne 8 di monete. La maggior difficolta' sta nel fatto che in questo quesito la soluzione e' unica. In quello delle 12 monete pare che comunque si suddividano le monete (considerando i modi piu' istintivi e non per esempio 6 gruppi da 2) si arrivi alla soluzione. Considerando le 8 monete no. Vi e' solo un unico procedimento.
Soluzione dettagliata.
Si dividiano le otto monete in due gruppi, gruppo A composto da sei monete e gruppo B composto dalle restanti due monete.
Considero per primo il gruppo A di sei monete e le suddivido in ulteriori due gruppi da tre che pongo sulla bilancia.
Ora considero i seguenti possibili casi.
-- Primo caso: i due gruppi da tre monete hanno lo stesso peso (prima pesata), allora utilizzo la seconda ed ultima pesata per determinare la moneta falsa dal gruppo B composto da due monete. Dunque ho determinato la moneta falsa in due pesate.
-- Secondo caso: uno tra i due gruppi di tre monete e' piu' leggero (prima pesata) dunque tra queste monete si nasconde quella falsa.
Prendo da questo gruppo di tre, due monete e considero i seguenti sotto casi:
---- Primo sotto caso: le due monete hanno lo stesso peso (seconda pesata) allora la terza moneta e' quella falsa. ---- Secondo sotto caso: una delle due monete e' piu' leggera (seconda pesata), dunque e' quella falsa.
Ho quindi determinato la moneta falsa in due sole pesate.
Come si puo' facilmente verificare la soluzione e' unica.
Grazie a Enrico Guastella per una soluzione equivalente ma molto più concisa e altrettanto chiara.
La mia idea per risolvere l'esercizio consiste nel togliere dal gruppo di otto monete due monete, e dividere le restanti sei in due gruppi da tre:
1) Nel caso i due gruppi da tre pesino uguale, la moneta falsa sta nelle due omesse che con l'ultima mossa possono essere confrontate.
2) Nel caso un gruppo risulti più leggero dell'altro, si esaminano solo due monete di quel gruppo e, nel caso esse siano uguali la moneta falsa è la terza, altrimenti la moneta falsa è la più leggera.
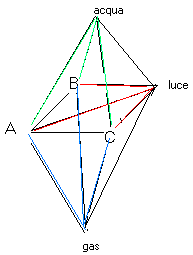
10. Le tre case e le tre fonti
E' stato dimostrato che questo problema non si può risolvere nel
piano, cioè nelle 2 dimensioni.
E' invece facile risolverlo nelle 3 dimensioni, sovrapponendo alcune linee.
Nella figura qui sotto le sovrapposizioni sono cerchiate.

Giorgio Dendi e Mouse mi hanno
comunicato che con un "trucco" abbastanza onesto si può risolvere il problema.
Riporto la soluzione di Mouse.
Vorrei dare una diversa soluzione (fantasiosa e un po truffaldina)
al quesito "Le tre case e le tre fonti".
Il trucco consiste nel far passare uno dei fili attraverso una delle
case/fonti.
Nessuna regola vieta infatti che questo avvenga.
Le linee devono stare sullo stesso piano e non si devo incrociare tra loro ma
non e' esplicitamente vietato che incrocino i "muri" delle case o delle fonti
;-)
Ringrazio il collega, prof. Fimiani Ugo per la seguente soluzione del problema delle tre case e delle tre fonti trovata da una allieva di classe prima della S.M.S "C. Nigra" di Torino (maggio 2005).
Ringrazio Enrico Ricci per la seguente soluzione.
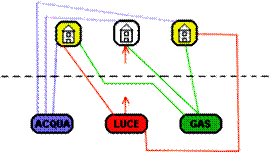
La soluzione potrebbe essere effettuando l'ultimo collegamento piegando il foglio o forandolo e facendo l'ultimo collegamento sul retro del foglio stesso.
11. I 9 punti e le 4 linee
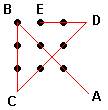
12. Il prigioniero
Chiamiamo A e B i due guardiani. Il prigioniero ne sceglie uno a caso,
poniamo A, e gli chiede:
"Se chiedessi al tuo collega B: "Qual è la porta che conduce alla salvezza?"
egli che cosa mi risponderebbe?"
Con questa domanda il prigioniero è sicuro di ottenere la risposta falsa e
perciò sceglierà l'altra porta!
Vediamo perché.
I casi sono due:
1° caso: A mente e B dice la verità: B risponderebbe la verità ma A che
mente riferisce il falso.
2° caso: A dice la verità e B mente: B risponderebbe il falso e A
riporta esattamente ciò che direbbe B, cioè, per l'appunto, il falso.
(Ringrazio Antonio Acquaviva per la seguente
precisazione)
La risposta si può spiegare anche con le tavola dell'algebra
booleana. Per le quali, posta la domanda che include le risposte di entrambi,
il risultato è falso in quanto
A(Vero)+ B(Falso) = Falso
A(Falso)+ B(Vero) = Falso.
13. C'è chi mente e chi dice la verità
(Risposta inviata da Emiliano C.)
Ho trovato una risposta che mi sembra accettabile, e volevo
sottoporla.
Il 3° uomo necessariamente mente: se dicesse la verità, i primi due uomini
sarebbero sposati e mentirebbero, quindi il 2° mentirebbe sostenendo che il 1°
ha detto che è scapolo; dunque il 1° avrebbe detto che è sposato, e ciò è
assurdo perché gli sposati mentono.
D'altra parte, se il 3° uomo mente, vuol dire che almeno uno degli altri due è
scapolo, dunque lo sono tutti e due, perché se lo fosse solo uno si cadrebbe di
nuovo nel paradosso appena esposto.
Quindi la soluzione è:
1° uomo: scapolo
2° uomo: scapolo
3° uomo: sposato
(Risposta inviata da Fernando Blanc)
La soluzione è nel primo uomo, il quale può solo aver affermato: "Sono
scapolo" (sia mentendo essendo cioè sposato, che dicendo la verità essendo cioè
scapolo).
Quindi avendo A necessariamente affermato: "Sono scapolo" conseguenzialmente B
dice la verità (è quindi scapolo), B dicendo la verità, conferma che A è
veramente scapolo (essendo scapoli A e B). C invece MENTE quindi è sposato. Non
vedo paradossi.
(Risposta inviata da Ettore
Saltarelli)
Secondo il mio parere, il problema ha due soluzioni distinte, in
particolare per quanto riguarda il primo uomo.
Infatti, concordo con il fatto che il primo debba necessariamente aver detto di
essere uno scapolo, che il secondo, dicendo la verità, sia uno scapolo, e che
il terzo, andando contro quanto detto dal secondo, sia uno sposato.
Ciò con cui non concordo è sul fatto che il primo uomo debba essere uno
scapolo.
Il secondo infatti ha semplicemente confermato che il primo ha detto di essere
uno scapolo, ma non ha confermato il fatto che il primo sia veramente uno
scapolo.
Quindi, riassumendo, il primo può essere sia uno scapolo che uno sposato, il
secondo è uno scapolo, il terzo è uno sposato.
(Risposta inviata da Velrio Bettini)
Si può risolvere partendo dal secondo tizio.
Egli può essere o scapolo o sposato.
Partiamo dal primo caso.
1 - Egli è scapolo quindi dice la verità. Da ciò deduciamo che anche il primo
tizio è scapolo (perché è vero ciò che dice il secondo e quindi vero anche
quello che dice il primo). Il terzo è invece uno sposato perché è falso che è
lui l'unico scapolo
2 - Egli è sposato quindi dice il falso. Quindi la frase detta dal primo tizio
è "io sono sposato". Se fosse vero mentirebbe quindi sarebbe uno scapolo. Se
fosse falso direbbe la verità quindi sarebbe uno sposato.
Da qui entriamo nel paradosso quindi l''unica soluzione possibile è la prima:
1-scapolo 2-scapolo 3-sposato.
(Risposta inviata da Egidio Dell'Atti)
Ritengo che si impossibile stabilire cosa sia il primo uomo.
Assodato che il secondo uomo è uno scapolo e il terzo uno sposato
ricordiamo che il secondo uomo riferisce "cosa ha detto" e non "cosa é"
il primo.
Il primo ha sicuramente detto di essere "scapolo" e quindi può essere:
* uno scapolo che dice la verità
oppure
* uno sposato che mente.
Rimane quindi incerta la determinazione della sua natura.
(Risposta inviata da Francesco
Viola)
Credo che la soluzione sia unica (primo uomo Sposato, secondo sposato, terzo
scapolo) e che tutte le soluzioni riportate nel sito siano erronee o comunque
travisino il testo, mi spiego:
Alla domanda se fosse o meno sposato il primo uomo ha risposto "Io sono cof..cof... po fkkjsdf8r... cof..." (in pratica con dei versi) così la risposta del secondo non può che essere Falsa (non gli è stato chiesto, infatti, se il primo uomo fosse o meno sposato ma cosa avesse detto e, quindi, l'unica risposta corretta sarebbe stata la riproduzione dei suoni del primo) quindi se la risposta del secondo uomo è falsa ciò comporta:
1. Il secondo uomo è sposato (mente, infatti)
2. Ciò che dice del secondo uomo è falso (anche il primo è quindi sposato)
3. Il terzo dice la verità (infatti non solo asserisce di essere scapolo ma di essere l'unico dei tre cosa che, dimostrata la falsità delle affermazioni precedenti non può che esser vera, quindi, il terzo uomo non mente ed è, appunto, scapolo).
Il precedente ragionamento è però passibile di due obbiezioni che tuttavia risultano essere false:
Obbiezione "A": "Ma il primo ha detto qualcosa, solo che l'intervistatore non ha capito".
Questa obiezione è nulla: nella lingua scritta ciò che è messo tra virgolette è ciò che viene effettivamente pronunciato, per descrivere la possibilità ventilata dall'obbiezione dovrebbe essere descritta con linguaggio indiretto (es. il primo uomo dice qualcosa di incomprensibile all'interlocutore); la lingua è una convenzione ma ha regole ben precise.
-Obbiezione "B": "E' vero il secondo non può essere che scapolo, in quanto mente, ma in fondo, proprio perché rispondeva alla domanda "che cosa ha detto il primo uomo?" rispondere "è scapolo" potrebbe essere una bugia nel significato/senso del contesto (in quanto NON è la risposta data il primo) che però esprime un predicato vero (il primo sarebbe per davvero scapolo e, alla domanda se lo fosse, il secondo avrebbe dovuto negarlo, mentendo, ma, essendogli stato chiesto cosa il primo avesse DETTO (e non cosa fosse), ha potuto mentire pur pronunciando un predicato di per sé vero: anche se il primo fosse stato scapolo NON è ciò che ha detto - sarebbe la logica seguita dal secondo)".
Questa obbiezione è molto più profonda della prima ma risulta esser anch'essa erronea. Analizziamo la premessa del quesito: "In una certa città gli uomini sposati mentono sempre e gli scapoli dicono sempre la verità". Tutto verte sul significato di "gli uomini sposati mentono sempre", se questo significasse che NON possono dire nulla di vero l'obbiezione cadrebbe da sé (anche mentendo sarebbe, per gli sposati, impossibile esprimere un predicato il cui concetto fosse vero), nel caso che volesse semplicemente dire che gli sposati non dicono la verità sembrerebbe, a prima vista (e solo a prima vista), che l'obbiezione sia corretta. Tuttavia se si attribuisse il secondo significato alla prima parte della premessa (cosa che comporta la considerazione separata di significato/senso e predicato rispetto a ciò che si afferma - so che i termini non sono tra i più appropriati ma da buon studente di economia sono digiuno di logica - e che si consideri falsa un'affermazione che lo sia anche solo nel significato/senso nonostante sia vera a livello di predicato) bisognerebbe considerare parimenti la seconda parte della premessa ("gli scapoli dicono SEMPRE la verità) e ciò che dice il primo uomo: ovvero se per creare una bugia basta che il significato/senso sia falso (pur essendo il predicato di per sé vero), per avere una verità entrambi devono essere veri (un po' come moltiplicare due numeri con segni opposti per ottenerne uno negativo rispetto alla necessità di moltiplicare due positivi, o di medesimo segno, per averne uno positivo) quindi la risposta del primo uomo è da considerarsi di per sé una menzogna (dice: "IO SONO cof..cof... po fkkjsdf8r... cof...") non basterebbe infatti che il significato/senso, che il primo uomo non riesce ad esprimere nel contesto, non fosse falso (in quanto non conoscibile e quindi forse vero e di scarso aiuto per la soluzione dell'enigma) ma sarebbe necessario che il predicato in sé fosse vero (ovvero il primo uomo dovrebbe dire sempre la verità e invece affermare di essere "cof..cof... po fkkjsdf8r... cof..." è una menzogna: l'uomo o è scapolo o sposato non è certo un insieme di suoni) cosa che non si verifica. Quindi, dimostrato che il primo uomo mente, questi può esser riconosciuto come sposato senza bisogno della prova fornita dall'affermazione, comunque falsa (anche se solo nel significato/senso del contesto), del secondo.
(Risposta inviata da Paolo Grandi)
Tale quesito è probabilmente mal posto...non ci sono dubbi su questo.
Dovrebbe essere, ad esempio, così:
"L'uomo NON si toglie il sigaro di bocca, e la sua risposta è incomprensibile per tutti, tranne che per il suo amico", e in tal caso sarebbe corretta la risposta fornita da Saltarelli e Dell'Atti, oppure così e co una giunta, susseguente alla risposta del secondo uomo...
"E lo è?" (altra domanda della turista) "Sì" (oppure "No").
O anche semplicemente "Ha detto che è scapolo, E COSI' E' (o MA NON E' COSI')".
Partendo da questa premessa, non è invece necessariamente vero quanto scritto da Viola...il narratore (figura estranea alla vicenda),non essendo chi proferisce le parole, riporta le stesse (i suoni, in questo caso), come le ha sentite o come le ha sentite chi gliele ha comunicate, cosa che smonta tutto il suointeressante ma tedioso ragionamento.
E se il narratore fosse un abitante di quella stessa città?
14. Di che colore è l'orso
L'orso è bianco.
Ngongo, infatti, si trova esattamente sul Polo Nord che è l'unico punto della
Terra in cui percorrendo un certo tratto verso sud, poi lo stesso tratto verso
est, poi lo stesso tratto verso nord, ci si ritrova al punto di partenza.
Ma, a ben pensarci, il Polo Nord non è l'unico punto della Terra in cui accade
questo strano fatto...
15. L'uomo nell'ascensore
L'uomo è un nano.
Non arriva a premere il pulsante del 10° piano. Se però c'è qualcun altro, si
fa aiutare.
16. Il lupo, la capra e il cavolo
Situazione iniziale: (- - - ... Pastore Lup Cap Cav)
1° viaggio: (- - Cap ... Pastore Lup Cav -): traghetta la capra e torna
indietro da solo.
2° viaggio: (- - Lup ... Pastore Cap Cav -): traghetta il lupo e porta indietro
la capra.
3° viaggio: (- Lup Cav ... Pastore Cap - -): traghetta il cavolo e torna
indietro da solo.
4° viaggio: (Lup Cap Cav Pastore ... - - -): traghetta la capra.
17. Un nome davvero singolare: Carlo
Giuseppe
18. Cin Cin
45 cin cin (se ognuno lo fa con ciascun altro una volta sola)
19. Una gallina e mezza
Una gallina e mezza fa un uovo al giorno, perciò in 6 giorni farà 6 uova.
Una gallina sola, in 6 giorni farà (2/3)*6 uova, cioè 4 uova.
20. L'asino e il mulo
L'asino portava 140 kg e il mulo 100 kg
Asino = a
Mulo = m
a + 20 = 2(m-20) = 2m - 40
m + 20 = a - 20
Ricavo a dalla prima equazione:
a = 2m - 60
Sostituisco nella seconda equazione:
m + 20 = 2m - 80
Ricavo:
m = 100
a = 140
Verifico:
Un asino disse a un mulo:"Se prendessi 20 Kg del tuo carico, il peso che mi
opprime diventerebbe il doppio del tuo".
Infatti: 140 + 20 = 2(100-20)
Il mulo rispose: "Se io prendessi 20 Kg del tuo peso, io porterei un carico
uguale al tuo".
Infatti: 100 + 20 = 140 - 20
Questo quesito ha anche un'altra interpretazione, secondo la quale l'asino portava 60 kg e il mulo 40 kg
21. Zampe e teste
18 conigli e 14 oche.
Una strategia risolutiva elementare è questa:
Essendoci 32 teste, se fossero tutte di oca, le zampe sarebbero 64.
Poiché invece ci sono 100 zampe, quelle in più sono senz'altro coppie di zampe
di conigli. Perciò i conigli sono:
(100-64)/2 = 36/2 = 18 conigli.
Dunque le oche sono 32-18 = 14 oche.
22. Dieci sacchetti da 10 monete
Risposta inviata da Francesco Marino.
Ci sono 9 sacchetti che contengono 10 monete da 1 g l'una e un
sacchetto che contiene 10 monete da 0,1 g perciò il peso complessivo dei
sacchetti sarebbe di (9*10*1) g+(1*10*0,1) g quindi in totale 91 g.
Ora, se noi togliessimo delle monete dai sacchetti con questo ordine:nessuna
dal primo sacchetto, 1 dal secondo, 2 dal terzo e via dicendo fino al decimo
sacchetto dal quale estrarremmo 9 monete noi sapremmo di aver eliminato dalla
pesata 45 monete .
Se le monete estratte fosse tutte di ugual peso, vale a dire da 1 grammo la
nostra pesata dovrebbe dare come risultato i 91 g totali meno i 45 g delle
monete estratte, ovvero 46 g.
Quindi potremmo calcolare prima della pesata l'ipotetico risultato per tutti i
casi di monete incriminate sottratte ai sacchetti con la semplice seguente
formula dove "n" sta per il numero di monete "incriminate" sottratte dal loro
sacchetto: 46+(n*1)-(n*0,1) e otterremmo i seguenti risultati: per nessuna
moneta estratta 46 g
per 1 moneta 46,9 g
per 2 monete 47,8 g
per 3 monete 48,7 g
per 4 monete 49,6 g
per 5 monete 50,5 g
per 6 monete 51,4 g
per 7 monete 52,3 g
per 8 monete 53,2 g
per 9 monete 54,1 g
Quindi una volta pesati i dieci sacchetti (sempre ipotizzando che i sacchetti
intesi come contenitori di monete non abbiano un peso) non ci resta che
confrontare la pesata con i risultati sopra ottenuti per sapere quante monete
sono state estratte dal sacchetto di monete più leggere .
Ancora più semplicemente si potrebbe dire che sarebbe sufficiente senza fare
calcoli osservare il valore decimale della pesata, difatti se il decimale fosse
pari a 0 ciò indicherebbe che il sacchetto con le monete leggere è quello dal
quale non è stata sottratta alcuna moneta mentre negli altri casi basterebbe
trovare il numero di decimali occorrenti a raggiungere l'intero successivo (ad
es. nel caso di un risultato come 49,6 g per giungere all'intero successivo
ossia in questo caso 50 servirebbero 4 decimi di grammo e siccome ogni moneta
leggera pesa 1 decimo di grammo il sacchetto dal dal sono state estratte 4
monete sarebbe quello incriminato).
Per quanto forse più rapida la seconda modalità preferisco la prima in quanto
se la bilancia utilizzata non avesse una precisione assoluta si rischierebbe di
commettere un errore (lo commetterebbe la bilancia) mentre calcolando il
risultato si avrebbe quasi 1 grammo di differenza tra un risultato e l'altro
lasciando una minore possibilità di errore (ovviamente approssimando la pesata
al risultato calcolato ad essa più vicina.
Nel caso in cui la bilancia sbagliasse così tanto la pesata da indurci in
errore allora forse sarebbe meglio prendere le monete dei sacchetti e andare a
comperare una bilancia nuova (consiglio una TANITA;-).
23. Attraversare il ponte
Ricordiamo i tempi di attraversamento indicando le quattro
persone con le iniziali dei rispettivi nomi:
Ecco la sequenza dei passaggi:
| Passano A e B, torna B | 2 + 2 = 4 min |
| Passano C e D, torna A | 10 + 1 = 11 min |
| Passano A e B | 2 min |
| Totale: 4 + 11 + 2 = 17 min |
24. Quattro triangoli con sei bastoncini
Con tre bastoncini formi un triangolo sul piano, unisci nello spazio le punte
degli altri tre bastoncini, in modo da formare un tetraedro; hai così ottenuto
4 triangoli.
Risposta inviata da Filippo Z., alunno di una scuola primaria di Bergamo.

25. Le 27 palline
Prepariamo tre gruppi di 9 palline ciascuno.
1° pesata: confrontando due di questi gruppi possiamo individuare in quale dei
tre gruppi (di 9 palline) si trova la pallina più pesante.
Prendiamo il gruppo incriminato e dividiamolo in tre gruppi di 3 palline
ciascuno.
2° pesata: confrontando due di questi gruppi possiamo individuare in quale dei
tre gruppi (di 3 palline) si trova la pallina più pesante.
Prendiamo il gruppo incriminato e dividiamolo in tre gruppi di 1 pallina
ciascuno.
3° pesata: confrontando due di queste palline possiamo individuare qual è la
pallina più pesante.
26. I 3 interruttori
Ecco il segreto: una lampadina può essere: accesa, spenta,
calda, fredda.
La procedura è la seguente.
Dopo aver compiuto queste operazioni entro immediatamente nella stanza, osservo e tocco la lampadina.
27. Con 7 bastoncini
Trasformo VII in "radice quadrata di I" spostando un bastoncino.
28. Un numero di 5 cifre
Il numero è 42857
Premetto 1: 142.857 * 3 = 428.571
Aggiungo 1 : 428.571
29. Il problema di Monthy Hall
Conviene cambiare.
Se NON cambiamo, abbiamo 1/3 di probabilità di vincere (perché abbiamo scelto 1
su 3).
Se cambiamo, abbiamo 2/3 di probabilità di vincere (perché scegliamo la porta
che faceva parte dei 2/3 sapendo però che dietro all'altra non c'è il premio ma
la capra).
Secondo quanto ci narra Paul Hoffman, la comprensione di questo
problema ha dato del filo da torcere persino al grande matematico Paul Erdos.
Se avete dei dubbi, consultate la pagina dedicata a: Il problema di Monthy Hall.
30. Parola d'ordine
La regola non consiste nel dire la metà del numero ma il numero di lettere da
cui è composto (in italiano)
Dunque la risposta a 4 (q-u-a-t-t-r-o) è 7.
31. I lupi mannari
Sono tre.
Esistono molte varianti di questo problema (L'isola dei cornuti, L'epidemia nel
convento, etc.)
e così è stato.
32. Un filo intorno alla Terra
Sì.
Il raggio della prima circonferenza è:
C/2pi (espresso in metri)
Il raggio della seconda circonferenza è:
(C+1)/2pi = C/(2pi) + 1/(2pi) (espresso in metri)
Dove pi = 3,14...
Come si vede, il secondo raggio è (1/2)pi più lungo del primo, in metri.
1/(2pi) = 1/6,283 = 0,159 m = 15,9 cm circa
Perciò la distanza fra la terra ed il filo, nel secondo caso è circa 15,9 cm e un gatto ci può passare.
In generale, se le lunghezze di due circonferenze qualsiasi
differiscono di 1 m, allora i raggi delle circonferenze differiscono di circa
15,9 cm.
Tale differenza fra i raggi è costante, indipendentemente dalle dimensioni
delle due circonferenze (ferma restando la loro differenza, che deve essere di
1 m).
33. Travasi
Nella seguente tabella sono riportati i contenuti dei tre recipienti in seguito
ad ogni travaso.
| Inizio | 1° trav. | 2° trav. | 3° trav. | 4° trav. | 5° trav. | 6° trav. | |
| Vaso da 3 dl | 0 | 0 | 3 | 0 | 2 | 2 | 3 |
| Vaso da 5 dl | 0 | 5 | 2 | 2 | 0 | 5 | 4 |
| Vaso da 8 dl | 8 | 3 | 3 | 6 | 6 | 1 | 1 |
34. Mozziconi di sigaretta
Trova 22 mozziconi e si fabbrica 5 sigarette.
Gli avanzano 5 + 2 = 7 mozziconi con cui si fabbrica 1 sigaretta.
Gli avanzano 1 + 3 mozziconi con i quali si fabbrica 1 sigaretta.
Gli avanza 1 mozzicone.
Ringrazio Mariangela Marcone per la
seguente simpatica analisi alternativa.
Per questo problema avrei trovato un'altra soluzione.
I mozziconi sono certo 22, ma, dato che non mi vedo il barbone intento a fare
troppi calcoli, procederei così:
Quindi 7*3 =21 +1 =22
Alla fine si sarà fumato anche l'unghia, ma mi sembra più semplice e in tema con il personaggio.
xhtml 1.1
Sito Web realizzato da Gianfranco Bo