[BASE Cinque - Appunti di
Matematica ricreativa]
La matematica come esplorazione
Cinque proposte di attività rivolte a studenti di tutte le età.
Care colleghe, cari colleghi, in questo articolo vi propongo cinque attività
che aiutano a capire come funziona l'esplorazione in Matematica e come é
collegata con l'immaginazione e la libertà. Sono adatte a diversi livelli
scolastici, a partire dal secondo ciclo della scuola primaria.
Se affrontiamo queste attività con lo spirito dell'esplorazione
matematica, arriviamo a sfiorare temi molto interessanti della ricerca
contemporanea.
Questo articolo è una relazione dettagliata di un seminario che ho tenuto al
27° Convegno Nazionale "Incontri con la Matematica" - Castel San Pietro Terme
(BO) - 2023.
1. Esplorazione, avventura, trucchi e fortuna in matematica
Francis Su, nel suo libro Mathematics for human flourishing ci ha mostrato in che modo la matematica é collegata con alcuni
bisogni umani fondamentali come l'esplorazione, il gioco, il combattimento e la libertà. (Su, 2019)
Il libro é stato tradotto in italiano e pubblicato nel
2023. (Su, 2023)
La parola esplorazione ci porta a pensare la matematica come un territorio (oppure un palazzo? un'astronave? un oceano?) da scoprire ma anche da costruire.
Come vi sentite quando cercate di risolvere un problema matematico davvero nuovo per voi?
Provate a confrontarvi con le sensazioni di Maryam Mirzakhani:
"I don't have any particular recipe," Mirzakhani said of her approach to developing new proofs. "It is the reason why doing research is challenging as well as attractive. It is like being lost in a jungle and trying to use all the knowledge that you can gather to come up with some new tricks, and with some luck you might find a way out. (Carey, 2014)
["E' come perdersi in una jungla e cercare di usare tutte le conoscenze che puoi mettere insieme per escogitare qualche nuovo trucco, e con un po' di fortuna potresti trovare una via d'uscita."]
Secondo questa visione, quando affrontiamo situazioni nuove in matematica e le
ricette precostituite non funzionano, abbiamo la libertà di inventare trucchi, modificare le domande e confidare persino nella fortuna.
2. Problemi normali versus compiti di esplorazione
Che differenza c'é tra un normale problema scolastico e una
proposta di esplorazione matematica?
La differenza principale é questa: i problemi indicano chiaramente ciò che viene dato e ciò che viene chiesto, mentre le esplorazioni contengono elementi di incertezza o apertura, e richiedono agli studenti un lavoro significativo di interpretazione della situazione e spesso di rielaborazione delle domande. (Da Ponte, 2005, 2014)
Ma forse la vera differenza sta nell'atteggiamento con cui un problema é affrontato piuttosto che nel modo in cui esso é formulato: quasi tutti i problemi possono essere un valido punto di partenza per avventurarsi nel mondo della matematica.
3. Da un lavoro fatto a scuola
|
SIMMETRIA - LIVELLO 1
1. Copiate (o fotocopiate) i due poligoni seguenti su un foglio di cartoncino.
2. Poi cercate di unirli in modo da formare un poligono che abbia un asse di simmetria.
3. Infine inventate voi stessi un puzzle simile a questo, formato da due o tre pezzi.
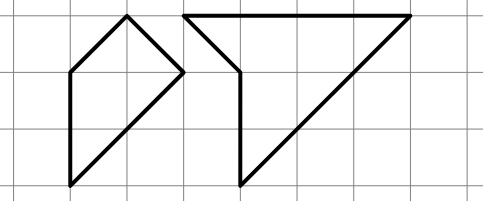
|
Possibili momenti dell'esplorazione.
- I due pezzi si possono sovrapporre? (no)
- Uno o entrambi i pezzi si possono ribaltare? (non sono previsti ribaltamenti, ma si può esplorare questa possibilità)
- Abbiamo trovato una soluzione, ma come possiamo dimostrare che la figura ottenuta é simmetrica?
- Abbiamo ottenuto due soluzioni. Sono entrambe accettabili?
- Se il lato di un quadrato della griglia A é lungo 1, quanto vale x?

- Come si può fare per inventare un nuovo puzzle di questo tipo? (un "trucco" é quello di disegnare prima una figura simmetrica e poi dividerla in pezzi)
4. Un puzzle minimalista di Vesa Timonen
Il puzzle seguente é una creazione di Vesa Timonen. La figura é una mia ricostruzione basata su un esemplare di legno, perciò potrebbe non essere esattamente uguale al progetto originale.
Vesa Timonen si definisce più o meno così, sul suo profllo LinkedIn (2023):
"Sono un designer di puzzle freelance. Il mio obiettivo é quello di progettare puzzle che diano alle persone momenti di aha, insegnino il pensiero logico ed esercitino resistenza e grinta."
|
SIMMETRIA - LIVELLO 2
1. Copiate (o fotocopiate) il puzzle seguente su un cartoncino e ritagliate i due pezzi.
2. Cercate di unire i due pezzi in modo da ottenere una figura simmetrica.
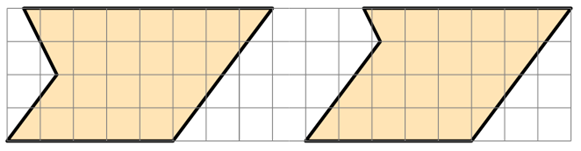
|
Possibili momenti dell'esplorazione.
- Dopo aver risolto il puzzle, confrontatelo con quello precedente e descrivete le difficoltà che avete incontrato.
- Se provate a rifarlo dopo qualche giorno, ci riuscite facilmente o incontrate le stesse difficolta?
---
La soluzione del puzzle è in fondo all'articolo.
---
5. Un puzzle di Tadao Kitazawa
L'esempio seguente é ispirato a una proposta di Tadao Kitazawa e può essere utile per scoprire la simmetria rotazionale. Nella richiesta infatti non si specifica che la simmetria debba essere solo assiale. Una delle tre soluzioni non ha un asse di simmetria ma un centro di simmetria. (Tadao Kitazawa, 2021, modificato)
|
SIMMETRIA - LIVELLO 3
1. Copiate (o fotocopiate) il puzzle seguente su un cartoncino e ritagliate i tre pezzi.
2. Mettete assieme i tre pezzi in modo da ottenere una figura simmetrica.
3. Il puzzle ha tre soluzioni: chi é capace di trovarle?
In una soluzione i pezzi vanno solo ruotati, nelle altre invece un pezzo va ribaltato.
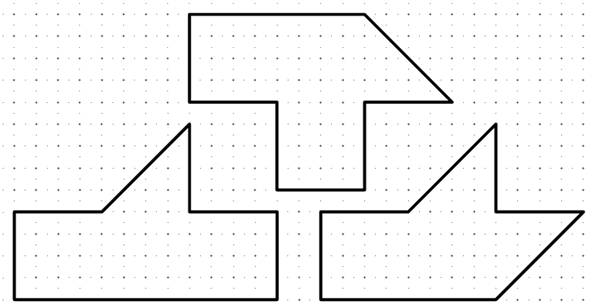
|
Questa esplorazione ci aiuta a comprendere temi legati alla ricerca matematica contemporanea, per esempio Erik Demaine e altri autori, nell'articolo Symmetric assembly puzzles are hard, beyond a few pieces, dimostrano che tale problema é fortemente NP-completo anche se i pezzi sono tutti polimini. (Erik Demaine e altri, 2020).
---
La soluzione del puzzle è in fondo all'articolo.
---
6. Esplorare un linguaggio formale: le espressioni aritmetiche
Le cosiddette espressioni aritmetiche sono forse l'unico caso meraviglioso in cui fin da bambini siamo messi a contatto con un linguaggio formale in piena regola. E' bene quindi imparare non solo a risolvere le espressioni applicando le regole del calcolo, ma anche a costruire mini-espressioni esplorando le regole convenzionali del linguaggio.
Uno spunto interessante é il problema dei "Quattro 4" (Soares, 2020).
|
I QUATTRO 4
Roberto ha dimostrato come si possono usare quattro 4, le operazioni aritmetiche e le parentesi per ottenere 20.

Utilizzando quattro 4, le operazioni matematiche che conoscete e le parentesi, siete capaci di ottenere tutti i numeri interi da 0 a 10?
|
Possibili momenti dell'esplorazione.
- Si possono usare i "4" come cifre, per esempio 44 : 4 + 4 = 15.
- Si possono usare altre operazioni come il fattoriale (4! = 24), la radice quadrata (√4 = 2) .
- Si può usare il punto decimale all'inizio di un numero senza lo zero iniziale, scoprendo che 4 : .4 = 10.
- Si può usare la notazione con parentesi per indicare i numeri periodici, scoprendo che 4 : .(4) = 9.
- Si possono usare anche altri numeri diversi dal 4 e diversi fra loro.
- Si può costruire una procedura, eventualmente informatica, che permetta di trovare un insieme più o meno grande di risultati possibili.
- Si può riflettere su come si fa per darsi delle regole e poi estenderle, ridurle oppure cambiarle e controllare se sono accettabili oppure no.
7. Usare una variabile: quanti triangoli?
L'ultima proposta é ispirata da alcuni giochi sui triangoli pubblicati da Giovanni Filocamo. (Filocamo 2022).
|
QUANTI TRIANGOLI CI SONO?
Osservate le figure.

1. Quanti triangoli ci sono nella figura 1? E nella figura 2? E nella 3?
2. Se la sequenza continua con lo stesso criterio, quanti triangoli ci saranno nella figura
n?
|
Possibili momenti dell'esplorazione.
- Capire che la prima intuizione non sempre é quella giusta.
- Questo é anche un problema combinatorio: come possiamo essere sicuri di aver contato tutti i casi possibili?
- Cosa significa una lettera dell'alfabeto in una formula matematica?
- Perché é utile usare le lettere invece dei numeri in una formula matematica?
In molti casi (nella scuola di base), la prima risposta che viene in mente non é quella giusta. L'errore porta a esplorare gli aspetti combinatori del conteggio.
La seconda parte apre uno spiraglio verso il mondo della pre-algebra (sempre nella scuola di base), con l'uso della lettera che rappresenta un numero variabile.
---
La soluzione è in fondo all'articolo.
---
8. Conclusione
Dicevo all'inizio che la cosa più importante per fare scoperte matematiche personali é l'atteggiamento da esploratore: non sai cosa troverai finché non parti, crea nuove possibilità, aspettati sorprese. Non importa se molti matematici sono già passati in quei luoghi. Ciò che importa davvero sono i tuoi passi sul sentiero che hai scelto e il tuo sguardo nel panorama che sta intorno.
---
Bibliografia
Carey, B. (2014). Stanford's Maryam Mirzakhani wins Fields Medal. Disponibile da: https://news.stanford.edu/2014/08/12/stanfords-maryam-mirzakhani-wins-fields-medal/
Da Ponte, J. P. (2005). Gestão curricular em Matemática. In GTI (Ed.), O professor e o desenvolvimento curricular (pp. 11-34). Lisboa: APM
Da Ponte, J. P., Branco, N., Quaresma, M. (2014). Exploratory Activity in the Mathematics Classroom. In Springer eBooks (pp. 103-125). Disponibile da: https://doi.org/10.1007/978-3-319-04993-9_7
Demaine, E., Korman, M., ... Uno, Y. (2019). Symmetric Assembly Puzzles are Hard, Beyond a Few Pieces. arXiv:1703.02671v2
Filocamo, G. (2022). La matematica si impara giocando. Curiosità e giochi di intelligenza pensati per chi (non) ama la matematica.
Kitazawa, T. (2021). Arithmetical, Geometrical and Combinatorial Puzzles from Japan. American Mathematical Soc.
Soares, N. V., & Pirola, N. A. (2020). Resolução de problemas e expressões numéricas: o quadro dos quatro quatros e o nunca dois e números binários. REMATEC. Revista De Matemática, Ensino E Cultura, 15(35), 163–177. Disponibile da: https://doi.org/10.37084/rematec.1980-3141.2020.n15.p163-177.id291
Su, F. (2020). Mathematics for Human Flourishing. Yale University Press
Su, F. (2023). Matematica per il fiorire dell'essere umano. Carocci editore
Soluzioni
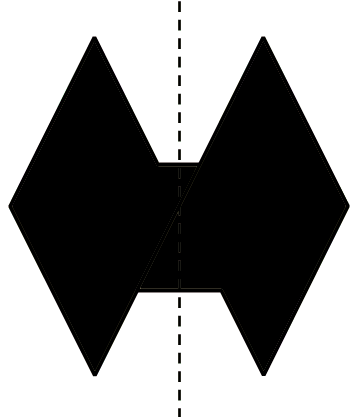
Simmetria - livello 2
Attenzione: nessun pezzo va ribaltato.

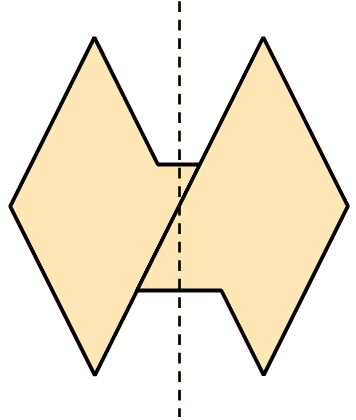
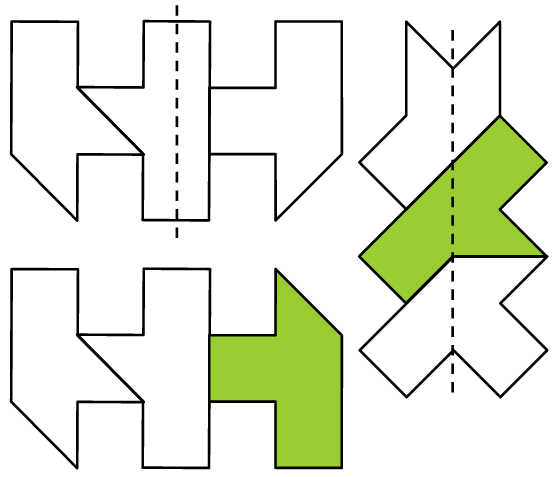
Simmetria - livello 3
Attenzione: nelle soluzioni, i pezzi colorati di verde sono ribaltati.
La terza soluzione è una simmetria rotazionale di 180°.


Quanti triangoli ci sono?

- figura 1: 1 triangolo;
- figura 2: 1+2 = 3 triangoli;
- figura 3: 1+2+3 = 6 triangoli;
- figura 4: 1+2+3+4 = 10 triangoli;
- ...
- figura n: n(n+1)/2 triangoli;
---
Pace e bene a tutti.
GfBo
Data creazione: giugno 2024
Ultimo aggiornamento: giugno 2024
html5
Sito Web realizzato da Gianfranco Bo









