[BASE Cinque - Appunti di Matematica ricreativa]

Mariti gelosi che devono attraversare un fiume con le loro mogli

Soluzione completa di un problema di attraversamento

Introduzione

Ringrazio innanzitutto Pietro Vitelli per questa soluzione dettagliata di un problema generale di attraversamento di un fiume.

Nella pagina Il leopardo, la capra e il kassawi trovate alcuni casi particolari che vi permetteranno di entrare nell'argomento.

Qui di seguito riporto un semplice esempio.

I tre mariti gelosi
Tre mariti e le rispettive tre mogli devono attraversare un fiume su una barca che può trasportare al massimo due persone alla volta.
Poiché i mariti sono molto gelosi, nessuna donna deve trovarsi mai assieme ad altri uomini se non in presenza del proprio marito.
Come faranno le tre coppie ad attraversare il fiume?

Attraversare un fiume: una possibile generalizzazione
Non poteva mancare un'indagine sul problema generale dell'attraversamento di un fiume. Non si sa mai: un giorno potremmo trovarci in 5000 ed è bene arrivare preparati.
Dunque, abbiamo:
- n coppie marito-moglie;
- una barca a x posti;
Possiamo farcela?
In quanti passaggi?
[Lucas, L'Arithmétique Amusante, 1895]

La soluzione generale

di Pietro Vitelli

Ultimamente mi sono appassionato all'argomento, grazie all'appendice sul tema, presente nel libro Giochi matematici alla corte di Carlomagno a cura di Raffaella Franci.
Da quest'ultima ho appreso che Lucas aveva trattato in modo completo il problema, nelle sue Ricreazioni Matematiche (1894).
Il problema sono le situazioni in cui, per un breve lasso di tempo (ad esempio avvicendamento tra barca e sponda), una moglie viene a trovarsi lontana dal proprio marito e in compagnia di altri uomini.
Io avevo a suo tempo considerato ambigue e comunque trascurabili queste situazioni.
In realtà esse non sono affatto ambigue e, semplicemente, non soddisfano la condizione iniziale della "gelosia".

Pertanto, riporto nel post seguente la corretta generalizzazione di Lucas, con l'aggiunta da parte mia delle dimostrazioni dei casi non esplicitati, e di quelli che Lucas rimanda al lettore.

In grassetto le mie dimostrazioni.

Seguendo l'approccio di Lucas, possiamo generalizzare il problema mediante elencazione di tutti i casi possibili con relativa dimostrazione.

Indichiamo con $Descrizione: Descrizione: Descrizione: n$ il numero di coppie (marito - moglie) da traghettare, e con $Descrizione: Descrizione: Descrizione: x$ il numero di posti sulla barca.

Ho individuato 10 casi possibili, che ricoprono tutte le casistiche, e sono:

$Descrizione: Descrizione: Descrizione: 2$ coppie - $Descrizione: Descrizione: Descrizione: 2$ posti

coppie - $Descrizione: Descrizione: Descrizione: 2$ posti

$Descrizione: Descrizione: Descrizione: 4$ coppie - $Descrizione: Descrizione: Descrizione: 2$ posti

$Descrizione: Descrizione: Descrizione: n$ coppie - $Descrizione: Descrizione: Descrizione: 2$ posti $Descrizione: Descrizione: Descrizione: \qquad n\/\ge\/5$

$Descrizione: Descrizione: Descrizione: 4$ coppie - posti

$Descrizione: Descrizione: Descrizione: 5$ coppie - posti

$Descrizione: Descrizione: Descrizione: n$ coppie - posti $Descrizione: Descrizione: Descrizione: \qquad n\/>\/5$

$Descrizione: Descrizione: Descrizione: n$ coppie - $Descrizione: Descrizione: Descrizione: 4$ posti $Descrizione: Descrizione: Descrizione: \qquad n\/\ge\/5$

$Descrizione: Descrizione: Descrizione: n$ coppie - $Descrizione: Descrizione: Descrizione: x$ posti $Descrizione: Descrizione: Descrizione: \qquad n\/\ge\/5$ , $Descrizione: Descrizione: Descrizione: \qquad x\/\ge\/4$ , $Descrizione: Descrizione: Descrizione: x$ pari, $Descrizione: Descrizione: Descrizione: \qquad n\/\ge\/x$

$Descrizione: Descrizione: Descrizione: n$ coppie - $Descrizione: Descrizione: Descrizione: x$ posti $Descrizione: Descrizione: Descrizione: \qquad n\/\ge\/5$ , $Descrizione: Descrizione: Descrizione: \qquad x\/\ge\/4$ , $Descrizione: Descrizione: Descrizione: x$ dispari, $Descrizione: Descrizione: Descrizione: \qquad n\/\ge\/x$

Quelli in testo normale sono stati dimostrati da Lucas; quelli in grassetto proverò a dimostrarli io.

Indichiamo con $Descrizione: Descrizione: Descrizione: A,\/B,\/C,\/\dots$ gli $Descrizione: Descrizione: Descrizione: n$ mariti, e con $Descrizione: Descrizione: Descrizione: a,\/b,\/c,\/\dots$ le $Descrizione: Descrizione: Descrizione: n$ mogli.
La situazione iniziale è la seguente:

$Descrizione: Descrizione: Descrizione: \text{Prima\/riva \hspace{20}Seconda\/riva}\\ \begin{array}{cccc} \/C & \qquad B & \qquad A & \hspace{45}\bullet & \qquad\bullet & \qquad\bullet \\ \/c & \qquad b & \qquad a & \hspace{45}\bullet & \qquad\bullet & \qquad\bullet \\ \end{array}$

Di seguito le dimostrazioni dei singoli casi.

2 coppie - 2 posti

$Descrizione: Descrizione: Descrizione: \fbox{\text{2 coppie - 2 posti}}$
Considerando che, dopo ogni viaggio, la barca approda alla seconda riva, si avrà

Le due mogli passano dall'altra parte
$Descrizione: Descrizione: Descrizione: \text{Prima\/riva \hspace{20}Seconda\/riva}\\ \begin{array}{cccc} \/\qquad B & \qquad A & \hspace{75}\Large{\bullet} & \qquad\Large{\bullet} \\ \/\qquad\Large{\bullet} & \qquad\Large{\bullet} & \hspace{75} b & \qquad a \\ \end{array}$

Una delle mogli ritorna, mentre i due mariti passano
$Descrizione: Descrizione: Descrizione: \text{Prima\/riva \hspace{20}Seconda\/riva}\\ \begin{array}{cccc} \/\qquad\Large{\bullet} & \qquad\Large{\bullet} & \hspace{75} B & \qquad A \\ \/\qquad b & \qquad\Large{\bullet} & \hspace{75}\Large{\bullet} & \qquad a \\ \end{array}$

La moglie sulla seconda riva ritorna a prendere l'altra moglie
$Descrizione: Descrizione: Descrizione: \text{Prima\/riva \hspace{20}Seconda\/riva}\\ \begin{array}{cccc} \/\qquad\Large{\bullet} & \qquad\Large{\bullet} & \hspace{75} B & \qquad A \\ \/\qquad\Large{\bullet} & \qquad\Large{\bullet} & \hspace{75} b & \qquad a \\ \end{array}$

3 coppie - 2 posti

$Descrizione: Descrizione: Descrizione: \fbox{\text{3 coppie - 2 posti}}$ (Lucas)
Considerando che, dopo ogni viaggio, la barca approda alla seconda riva, si avrà

Due mogli passano dall'altra parte
$Descrizione: Descrizione: Descrizione: \text{Prima\/riva \hspace{20}Seconda\/riva}\\ \begin{array}{cccc} \/C & \qquad B & \qquad A & \hspace{45}\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} \\ \/c & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \hspace{45}\Large{\bullet} & \qquad b & \qquad a \\ \end{array}$

Una delle mogli torna e porta sull'altra riva la terza
$Descrizione: Descrizione: Descrizione: \text{Prima\/riva \hspace{20}Seconda\/riva}\\ \begin{array}{cccc} \/C & \qquad B & \qquad A & \hspace{45}\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} \\ \/\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \hspace{45} c & \qquad b & \qquad a \\ \end{array}$

Una delle mogli ritorna, resta con suo marito, mentre gli altri due mariti passano
$Descrizione: Descrizione: Descrizione: \text{Prima\/riva \hspace{20}Seconda\/riva}\\ \begin{array}{cccc} \/ C & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \hspace{45}\Large{\bullet} & \qquad B & \qquad A \\ \/ c & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \hspace{45} \Large{\bullet} & \qquad b & \qquad a \\ \end{array}$

Un marito torna assieme alla moglie, che lascia a riva mentre porta dall'altra parte l'altro marito
$Descrizione: Descrizione: Descrizione: \text{Prima\/riva \hspace{20}Seconda\/riva}\\ \begin{array}{cccc} \/\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \hspace{45}\Large{\bullet} & \qquad B & \qquad A \\ \/ c & \qquad b & \qquad\Large{\bullet} & \hspace{45} \Large{\bullet} & \qquad\Large{\bullet} & \qquad a \\ \end{array}$

La moglie che ha appena attraversato il fiume ritorna a prendere una delle altre due
$Descrizione: Descrizione: Descrizione: \text{Prima\/riva \hspace{20}Seconda\/riva}\\ \begin{array}{cccc} \/\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \hspace{45}\Large{\bullet} & \qquad B & \qquad A \\ \/ c & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \hspace{45} \Large{\bullet} & \qquad b & \qquad a \\ \end{array}$

Una moglie (o il marito) ritorna a prendere l'ultima
$Descrizione: Descrizione: Descrizione: \text{Prima\/riva \hspace{20}Seconda\/riva}\\ \begin{array}{cccc} \/ \Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \hspace{45} C & \qquad B & \qquad A \\ \/ \Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \hspace{45} c & \qquad b & \qquad a \\ \end{array}$

4 coppie - 2 posti

$Descrizione: Descrizione: Descrizione: \fbox{\text{4 coppie - 2 posti}}$ (Lucas)
Ecco come si può dimostrare l'impossibilità di questo problema quando non è possibile far passare più di due persone alla volta.
Prima di tutto, va osservato che, tra un passaggio e l'altro, il numero delle persone passate, se aumenta, non può che aumentare di un'unità.
Di conseguenza, possiamo supporre che si facciano passare due, poi tre, poi quattro persone assecondando le condizioni imposte, e vediamo se queste possono essere verificate anche quando sono passate cinque persone.
Queste cinque persone non possono trovarsi che in una delle quattro condizioni seguenti:

$Descrizione: Descrizione: Descrizione: \begin{array}{cccc} \text{4 donne} & \hspace{45}\text{3 donne} & \hspace{45}\text{2 donne} & \hspace{45}\text{1 donna}\\ \text{1 uomo} & \hspace{45}\text{2 uomini} & \hspace{45}\text{3 uomini} & \hspace{45}\text{4 uomini} \end{array}$

I due primi casi sono impossibili, perchè contraddicono l'enunciazione del problema, dato che sulla seconda riva, le donne sono in maggiornaza e, di conseguenza, almeno una si trova in compagnia di un altro uomo senza il marito;
allo stesso modo è impossibile il terzo caso, perchè questa volta le donne si trovano in maggioranza sulla prima riva.
Quanto all'ultimo caso, può aver luogo solo se nell'ultimo attraversamento sono stati portati due uomini oppure un uomo e una donna.
In realtà, non è possibile che siano stati portati due uomini, poichè sull'altra riva sarebbero rimasti due uomini e tre donne, con una situazione analoga a quella del secondo caso;
nè è possibile che siano stati trasportati un uomo e una donna, perchè sulla prima riva sarebbero rimasti un uomo e quattro donne, situazione quindi analoga al primo caso.
Dunque, seguendo le condizioni poste dall'enunciato del problema, non è possibile far transitare cinque persone.

n coppie - 2 posti

$Descrizione: Descrizione: Descrizione: \fbox{n\text{ coppie - 2 posti}\qquad\qquad n\/\ge\/5}$
Possiamo utilizzare lo stesso ragionamento utilizzato da Lucas per il caso precedente (4 coppie - 2 posti).
Di conseguenza, possiamo supporre che si facciano passare due, poi tre, fin a $Descrizione: Descrizione: Descrizione: x$ persone assecondando le condizioni imposte, e vediamo se queste possono essere verificate anche quando sono passate $Descrizione: Descrizione: Descrizione: x+1$ persone.
Per la dimostrazione, consideriamo un $Descrizione: Descrizione: Descrizione: x\/\ge\/n$ , e pari; ossia $Descrizione: Descrizione: Descrizione: x\/=\/n\/+\/2k$ , con $Descrizione: Descrizione: Descrizione: k\/=\/1,2,3,...,n$ .

Dunque, queste $Descrizione: Descrizione: Descrizione: x+1$ persone possono trovarsi in una delle $Descrizione: Descrizione: Descrizione: n$ condizioni seguenti:

$Descrizione: Descrizione: Descrizione: \begin{array}{cccc} \text{x donne} & \hspace{45}\text{x-1 donne} & \hspace{45}\text{x-2 donne} & \hspace{45}\cdots & \hspace{45}\text{3 donna}& \hspace{45}\text{2 donna}& \hspace{45}\text{1 donna}\\ \text{1 uomo} & \hspace{45}\text{2 uomini} & \hspace{45}\text{3 uomini} & \hspace{45}\cdots & \hspace{45}\text{x-2 uomini} & \hspace{45}\text{x-1 uomini} & \hspace{45}\text{x uomini}\end{array}$

Essendo $Descrizione: Descrizione: Descrizione: x$ pari, si ha che:
i primi $Descrizione: Descrizione: Descrizione: \frac{x}{2}$ casi sono impossibili, perchè contraddicono l'enunciazione del problema, dato che sulla seconda riva, le donne sono in maggioranza e, di conseguenza, almeno una si trova in compagnia di un altro uomo senza il marito;
allo stesso modo sono impossibili i successivi $Descrizione: Descrizione: Descrizione: \frac{x}{2}-1$ casi, perchè questa volta le donne si trovano in maggioranza sulla prima riva.
Quanto all'ultimo caso, può aver luogo solo se nell'ultimo attraversamento sono stati portati due uomini oppure un uomo e una donna.
In realtà, non è possibile che siano stati portati due uomini, poiché sull'altra riva sarebbero rimasti $Descrizione: Descrizione: Descrizione: 2$ uomini e $Descrizione: Descrizione: Descrizione: x-1$ donne, con una situazione analoga a quella del secondo caso;
nè è possibile che siano stati trasportati un uomo e una donna, perchè sulla prima riva sarebbero rimasti $Descrizione: Descrizione: Descrizione: 1$ uomo e $Descrizione: Descrizione: Descrizione: x$ donne, situazione quindi analoga al primo caso.
Dunque, seguendo le condizioni poste dall'enunciato del problema, non è possibile far transitare $Descrizione: Descrizione: Descrizione: x+1$ persone, ed il problema è pertanto non risolvibile.

4 coppie - 3 posti

$Descrizione: Descrizione: Descrizione: \fbox{\text{4 coppie - 3 posti}}$ (Lucas - Labosne)

All'inizio passano tre donne
$Descrizione: Descrizione: Descrizione: \text{Prima\/riva \hspace{70}Seconda\/riva}\\ \begin{array}{cccc} \/ D & \qquad C & \qquad B & \qquad A & \hspace{45}\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} \\ \/ d & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \hspace{45} \Large{\bullet} & \qquad c & \qquad b & \qquad a \\ \end{array}$

Una donna (o due) ritornano per portare sulla seconda riva la quarta
$Descrizione: Descrizione: Descrizione: \text{Prima\/riva \hspace{70}Seconda\/riva}\\ \begin{array}{cccc} \/ D & \qquad C & \qquad B & \qquad A & \hspace{45}\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} \\ \/\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \hspace{45} d & \qquad c & \qquad b & \qquad a \\ \end{array}$

Una delle donne ritorna, resta con suo marito, mentre passano gli altri tre uomini
$Descrizione: Descrizione: Descrizione: \text{Prima\/riva \hspace{70}Seconda\/riva}\\ \begin{array}{cccc} \/ D & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \hspace{45}\Large{\bullet} & \qquad C & \qquad B & \qquad A \\ \/ d & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \hspace{45}\Large{\bullet} & \qquad c & \qquad b & \qquad a \\ \end{array}$

Uno dei mariti ritorna assieme alla moglie e porta sulla seconda riva l'ultimo marito
$Descrizione: Descrizione: Descrizione: \text{Prima\/riva \hspace{70}Seconda\/riva}\\ \begin{array}{cccc} \/\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \hspace{45} D & \qquad C & \qquad B & \qquad A \\ \/ d & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \hspace{45}\Large{\bullet} & \qquad c & \qquad b & \qquad a \\ \end{array}$

Infine, l'ultimo dei mariti torna a prendere sua moglie
$Descrizione: Descrizione: Descrizione: \text{Prima\/riva \hspace{70}Seconda\/riva}\\ \begin{array}{cccc} \/\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \hspace{45} D & \qquad C & \qquad B & \qquad A \\ \/\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \hspace{45} d & \qquad c & \qquad b & \qquad a \\ \end{array}$

5 coppie - 3 posti

$Descrizione: Descrizione: Descrizione: \fbox{\text{5 coppie - 3 posti}}$ (Lucas - Delannoy)
Considerando che, dopo ogni viaggio, la barca approda alla seconda riva, si avrà

Tre donne passano per prime
$Descrizione: Descrizione: Descrizione: \text{Prima\/riva \hspace{100}Seconda\/riva}\\ \begin{array}{cccc} \/E & \qquad D & \qquad C & \qquad B & \qquad A & \hspace{45}\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} \\ \/e & \qquad d & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \hspace{45}\Large{\bullet} & \qquad\Large{\bullet} & \qquad c & \qquad b & \qquad a \\ \end{array}$

Una donna (o due) torna indietro e porta la quarta sulla seconda riva
$Descrizione: Descrizione: Descrizione: \text{Prima\/riva \hspace{100}Seconda\/riva}\\ \begin{array}{cccc} \/E & \qquad D & \qquad C & \qquad B & \qquad A & \hspace{45}\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} \\ \/e & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \hspace{45}\Large{\bullet} & \qquad d & \qquad c & \qquad b & \qquad a \\ \end{array}$

Una delle donne ritorna, e tre mariti raggiungono le rispettive mogli
$Descrizione: Descrizione: Descrizione: \text{Prima\/riva \hspace{100}Seconda\/riva}\\ \begin{array}{cccc} \/E & \qquad D & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \hspace{45}\Large{\bullet} & \qquad\Large{\bullet} & \qquad C & \qquad B & \qquad A \\ \/e & \qquad d & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \hspace{45}\Large{\bullet} & \qquad\Large{\bullet} & \qquad c & \qquad b & \qquad a \\ \end{array}$

Una delle coppie ritorna, mentre passano gli altri tre mariti
$Descrizione: Descrizione: Descrizione: \text{Prima\/riva \hspace{100}Seconda\/riva}\\ \begin{array}{cccc} \/\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \hspace{45} E & \qquad D & \qquad C & \qquad B & \qquad A \\ \/e & \qquad d & \qquad c & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \hspace{45}\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \qquad b & \qquad a \\ \end{array}$

Una delle mogli ritorna e porta altre due mogli sulla seconda riva
$Descrizione: Descrizione: Descrizione: \text{Prima\/riva \hspace{100}Seconda\/riva}\\ \begin{array}{cccc} \/\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \hspace{45} E & \qquad D & \qquad C & \qquad B & \qquad A \\ \/e & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \hspace{45}\Large{\bullet} & \qquad d & \qquad c & \qquad b & \qquad a \\ \end{array}$

Una moglie (o il marito) ritorna a prendere l'ultima
$Descrizione: Descrizione: Descrizione: \text{Prima\/riva \hspace{100}Seconda\/riva}\\ \begin{array}{cccc} \/\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \hspace{45} E & \qquad D & \qquad C & \qquad B & \qquad A \\ \/\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \hspace{45} e & \qquad d & \qquad c & \qquad b & \qquad a \\ \end{array}$

n coppie - 3 posti

$Descrizione: Descrizione: Descrizione: \fbox{n\text{ coppie - 3 posti}\qquad\qquad n\/>\/5}$
Possiamo utilizzare lo stesso ragionamento utilizzato per il caso di ( $Descrizione: Descrizione: Descrizione: n\text{ coppie - 2 posti}\qquad\qquad n\/\ge\/5$ ).
In questo caso, però, va osservato che, tra un passaggio e l'altro, il numero delle persone passate, se aumenta, può aumentare sia di un'unità, che di due.
Di conseguenza, possiamo supporre che si facciano passare due, poi tre, fino a $Descrizione: Descrizione: Descrizione: n$ persone assecondando le condizioni imposte, e vediamo se queste possono essere verificate anche quando sono passate , ed persone.

Supponiamo, per comodità, che $Descrizione: Descrizione: Descrizione: n$ sia pari.

Situazione con persone sulla seconda riva:

queste persone possono trovarsi in una delle $Descrizione: Descrizione: Descrizione: n$ condizioni seguenti:

$Descrizione: Descrizione: Descrizione: \begin{array}{cccc}\text{n donne} & \hspace{45}\text{n-1 donne} & \hspace{45}\text{n-2 donne} & \hspace{45}\cdots & \hspace{45}\text{3 donna}& \hspace{45}\text{2 donna}& \hspace{45}\text{1 donna}\\\text{1 uomo} & \hspace{45}\text{2 uomini} & \hspace{45}\text{3 uomini} & \hspace{45}\cdots & \hspace{45}\text{n-2 uomini} & \hspace{45}\text{n-1 uomini} & \hspace{45}\text{n uomini}\end{array}$

i primi $Descrizione: Descrizione: Descrizione: \frac{n}{2}$ casi sono impossibili, perchè contraddicono l'enunciazione del problema, dato che sulla seconda riva, le donne sono in maggioranza e, di conseguenza, almeno una si trova in compagnia di un altro uomo senza il marito;
allo stesso modo sono impossibili i successivi $Descrizione: Descrizione: Descrizione: \frac{n}{2}-1$ casi, perchè questa volta le donne si trovano in maggioranza sulla prima riva.
Quanto all'ultimo caso, può aver luogo solo se nell'ultimo attraversamento sono stati portati tre uomini oppure due uomini e una donna.
In realtà, non è possibile che siano stati portati tre uomini, poiché sull'altra riva sarebbero rimasti uomini e donne, ossia una o più donne senza il proprio marito;
nè è possibile che siano stati trasportati due uomini e una donna, perchè sulla prima riva sarebbero rimasti $Descrizione: Descrizione: Descrizione: 2$ uomini e $Descrizione: Descrizione: Descrizione: n$ donne, situazione analoga alla precedente.
Dunque, seguendo le condizioni poste dall'enunciato del problema, non è possibile far transitare persone.

Tuttavia, sempre assecondando le condizioni imposte, potrebbe essere possibile passare direttamente, da $Descrizione: Descrizione: Descrizione: n$ persone ad persone; pertanto analizziamo anche la situazione con persone sulla seconda riva.

Situazione con persone sulla seconda riva:

queste persone possono trovarsi in una delle condizioni seguenti:

$Descrizione: Descrizione: Descrizione: \begin{array}{cccc}\text{n+1 donne} & \hspace{45}\text{n donne} & \hspace{45}\text{n-1 donne} & \hspace{45}\cdots & \hspace{45}\text{3 donna}& \hspace{45}\text{2 donna}& \hspace{45}\text{1 donna}\\\text{1 uomo} & \hspace{45}\text{2 uomini} & \hspace{45}\text{3 uomini} & \hspace{45}\cdots & \hspace{45}\text{n-1 uomini} & \hspace{45}\text{n uomini} & \hspace{45}\text{n+1 uomini}\end{array}$

i primi $Descrizione: Descrizione: Descrizione: \frac{n}{2}$ casi sono impossibili, perchè contraddicono l'enunciazione del problema, dato che sulla seconda riva, le donne sono in maggioranza e, di conseguenza, almeno una si trova in compagnia di un altro uomo senza il marito;
allo stesso modo sono impossibili gli ultimi $Descrizione: Descrizione: Descrizione: \frac{n}{2}-1$ casi, perchè questa volta le donne si trovano in maggioranza sulla prima riva.
L'ultimo caso, analogamente a quanto scritto per l'ultimo caso della situazione con persone sulla seconda riva, è impossibile.
Resta da dimostrare l'impossibilità del caso centrale, ossia il caso in cui si ha lo stesso numero di uomini e donne sulla seconda riva, ossia:

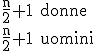
$Descrizione: Descrizione: Descrizione: \begin{array}{cccc}\large{\text{\frac{n}{2}+1 donne} \\ \text{\frac{n}{2}+1 uomini}} \end{array}$

Questo caso, può aver luogo solo se nell'ultimo attraversamento sono stati portati tre uomini, tre donne oppure due uomini e una donna.
In realtà, non è possibile che siano stati portati tre uomini, poiché, in tal caso, sulla seconda riva sarebbero già presenti $Descrizione: Descrizione: Descrizione: \frac{n}{2}-2$ uomini e $Descrizione: Descrizione: Descrizione: \frac{n}{2}+1$ donne, ossia tre donne senza il proprio marito;
altresì non è possibile che siano stati trasportati due uomini e una donna, poiché, in tal caso, sulla seconda riva sarebbero già presenti $Descrizione: Descrizione: Descrizione: \frac{n}{2}-1$ uomini e $Descrizione: Descrizione: Descrizione: \frac{n}{2}$ donne, ossia una donna senza il proprio marito;
Infine non è possibile che siano state portate tre donne, poiché sull'altra riva sarebbero rimasti $Descrizione: Descrizione: Descrizione: \frac{n}{2}-1$ uomini e $Descrizione: Descrizione: Descrizione: \frac{n}{2}+2$ donne, ossia tre donne senza il proprio marito.

Dunque, seguendo le condizioni poste dall'enunciato del problema, non è possibile far transitare né persone, né persone; pertanto il problema non è risolvibile.

n coppie - x posti (prima parte)

$Descrizione: Descrizione: Descrizione: \fbox{n\text{ coppie - }x\text{ posti}\qquad\qquad n\/\ge\/5\/,\/x\/\ge\/4\/,\/x\text{ pari}\/,\/n\/\ge\/x}$

Il ragionamento è il seguente:

si fanno passare $Descrizione: Descrizione: Descrizione: \large\frac{x}{2}$ coppie alla volta sulla seconda riva, mentre una coppia ritorna indietro per permettere l'attraversamento alle altre coppie.
Ripetendo questa manovra, si verifica facilmente che le $Descrizione: Descrizione: Descrizione: \large n$ coppie possono attraversare il fiume in $Descrizione: Descrizione: Descrizione: \Large{\left\lceil\frac{n-1}{\frac{x}{2}-1}\right\rceil}$ viaggi.

n coppie - x posti (seconda parte)

$Descrizione: Descrizione: Descrizione: \fbox{n\text{ coppie - }x\text{ posti}\qquad\qquad n\/\ge\/5\/,\/x\/\ge\/4\/,\/x\text{ dispari}\/,\/n\/\ge\/x}$
Passano $Descrizione: Descrizione: Descrizione: \large x$ mogli sulla seconda riva;
una delle mogli torna, resta con il marito, mentre altri $Descrizione: Descrizione: Descrizione: \large x$ mariti passano sulla seconda riva;
una coppia torna indietro, ed altre $Descrizione: Descrizione: Descrizione: \large\frac{x-1}{2}$ coppie raggiungono la seconda riva;
ripetendo questa manovra si fanno passare tutte le restanti coppie.

Calcoliamo, adesso, il numero di viaggi che vengono effettuati;
dopo $Descrizione: Descrizione: Descrizione: 2$ viaggi abbiamo la seguente situazione

$Descrizione: Descrizione: Descrizione: \text{Prima\/riva \hspace{100}Seconda\/riva}\\ n-x+1\;\text{coppie}\hspace{100} x-1\;\text{coppie}$

dopo di che una coppia torna indietro e si ottiene la seguente situazione

$Descrizione: Descrizione: Descrizione: \text{Prima\/riva \hspace{100}Seconda\/riva}\\ n-x+2\;\text{coppie}\hspace{100} x-2\;\text{coppie}$

a questo punto abbiamo $Descrizione: Descrizione: Descrizione: \large n-x+2$ coppie che passano sulla seconda riva, $Descrizione: Descrizione: Descrizione: \large\frac{x-1}{2}$ alla volta;
stando a quanto calcolato nel caso precedente, il numero di viaggi necessario per far passare $Descrizione: Descrizione: Descrizione: \large n-x+2$ coppie, $Descrizione: Descrizione: Descrizione: \large\frac{x-1}{2}$ alla volta, sarà pari a

$Descrizione: Descrizione: Descrizione: \large\left\lceil \frac{n-x+2-1}{\left(\frac{x-1}{2}\right)-1}\right\rceil \qquad\Rightarrow\qquad \left\lceil \frac{n-x+1}{\left(\frac{x-1}{2}\right)-1}\right\rceil$

Quindi le $Descrizione: Descrizione: Descrizione: n$ coppie possono attraversare il fiume in un totale di $Descrizione: Descrizione: Descrizione: \qquad\large 2+\left\lceil\frac{n-x+1}{\left(\frac{x-1}{2}\right)-1}\right\rceil\qquad$ viaggi.

3 coppie - 3 posti

$Descrizione: Descrizione: Descrizione: \fbox{\text{3 coppie - 3 posti}}$
Considerando che, dopo ogni viaggio, la barca approda alla seconda riva, si avrà

Le tre mogli passano dall'altra parte
$Descrizione: Descrizione: Descrizione: \text{Prima\/riva \hspace{20}Seconda\/riva}\\ \begin{array}{cccc} \/C & \qquad B & \qquad A & \hspace{45}\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} \\ \/\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \hspace{45}c & \qquad b & \qquad a \\ \end{array}$

Una delle mogli ritorna, mentre i tre mariti passano
$Descrizione: Descrizione: Descrizione: \text{Prima\/riva \hspace{20}Seconda\/riva}\\ \begin{array}{cccc} \/\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \hspace{50} C & B & A \\ \/c & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \hspace{45}\Large{\bullet} & \qquad b & \qquad a \\ \end{array}$

Una delle mogli sulla seconda riva ritorna a prendere l'ultima moglie sulla prima riva
$Descrizione: Descrizione: Descrizione: \text{Prima\/riva \hspace{20}Seconda\/riva}\\ \begin{array}{cccc} \/\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \hspace{45} C & B & A \\ \/\Large{\bullet} & \qquad\Large{\bullet} & \qquad\Large{\bullet} & \hspace{45} c & \qquad b & \qquad a \\ \end{array}$

Data creazione: aprile 2012

Ultimo aggiornamento: aprile 2012

xhtml 1.0

Sito Web realizzato da Gianfranco Bo