
[BASE Cinque - Appunti di Matematica ricreativa]
Idee da un problema di Samuel Loyd
Un'auto per nove amici
Nove amici vogliono andare al mare, in una bellissima spiaggia distante 26
km.
Purtroppo una delle due auto a loro disposizione è guasta e perciò devono
utilizzare una sola auto, che è omologata per 5 persone.
Gli amici si dividono in due gruppi. di 5 e 4 persone. L'auto porta a
destinazione il primo gruppo e poi una persona torna indietro a prendere
l'altro gruppo.
Per non perdere tempo, il secondo gruppo inizia il tragitto a piedi.
Questa è una buona strategia, ma ne esiste una migliore? Quale?
Sappiate che:
Un tandem per tre
Tre amici, Aldo, Baldo e Carlo devono percorrere una strada lunga 40 km.
Hanno a disposizione un tandem con il quale due persone potrebbero completare
il viaggio in un'ora.
Non possono stare in tre sul tandem.
Perciò decidono di organizzarsi: ciascuno di essi andrà un po' a piedi e un
po' sul tandem.
Le loro velocità a piedi sono le seguenti:
Qual è il tempo minimo in cui i tre potranno percorrere i 40 km del viaggio?
Una bicicletta per due
Due amici devono percorrere 30 km e hanno una sola bicicletta a
disposizione.
Come possono organizzarsi per arrivare a destinazione nel più breve tempo possibile?
Nota storica
Il problema del tandem è tratto da Samuel Loyd, Cyclopedia, 1914, p. 322.
Ecco una riproduzione dell'originale.

Esiste una versione precedente di questo problema, dovuta a: C. A. Laisant, Initiation Mathématique, Georg, Geneva & Hachette, Paris, 1906.
Chap. 51: Deux cyclistes pour une bicyclette, pp. 127-129. Graphic solution, assuming walking speeds and riding speeds are equal, but notes one can deal with the more general problem with a little more mathematics.
Chap. 52: La voiture insuffisante, pp. 129-132. Two couples, but the car can only carry two persons besides the driver. Graphic solution, again assuming walking speeds and driving speeds are equal, but making an estimate for calculational convenience. He also states the exact solution.
Data creazione: gennaio 2006
Ultimo aggiornamento: gennaio 2006
Un'auto per nove amici
Nove amici vogliono andare al mare, in una bellissima spiaggia distante 26
km.
Purtroppo una delle due auto a loro disposizione è guasta e perciò devono
utilizzare una sola auto, che è omologata per 5 persone.
Gli amici si dividono in due gruppi. di 5 e 4 persone. L'auto porta a
destinazione il primo gruppo e poi una persona torna indietro a prendere
l'altro gruppo.
Per non perdere tempo, il secondo gruppo inizia il tragitto a piedi.
Questa è una buona strategia, ma ne esiste una migliore? Quale?
Sappiate che:
Un tandem per tre
Tre amici, Aldo, Baldo e Carlo devono percorrere una strada lunga 40 km.
Hanno a disposizione un tandem con il quale due persone potrebbero completare
il viaggio in un'ora.
Non possono stare in tre sul tandem.
Perciò decidono di organizzarsi: ciascuno di essi andrà un po' a piedi e un
po' sul tandem.
Le loro velocità a piedi sono le seguenti:
Qual è il tempo minimo in cui i tre potranno percorrere i 40 km del viaggio?
Un particolare ringraziamento a Franco per i notevoli contributi dati alla risoluzione di questo problema
Il diagramma seguente illustra una possibile soluzione con 2 dietro-front del tandem.
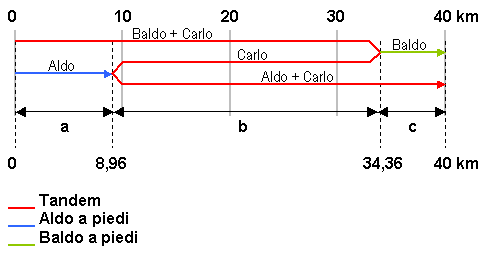
Il sistema risolvente è:
Nota: i tre T (tempi) sono uguali)
Le soluzioni esatte sono:
La situazione è descritta analiticamente molto bene dal seguente grafico spazio-tempo inviato da Franco al Forum.
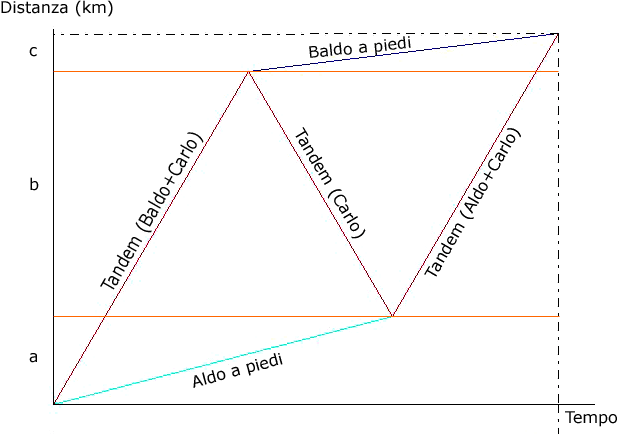
Enrico Delfini ha proposto la seguente soluzione:
Come suggerimenti generici, direi che:
Come prima approccio istintivo mi viene da propporre (senza quantificare le distanze):
Questo schema mi sembra efficiente perchè mi pare quello in cui A cammina per più tempo.
Restano da individuare i due punti di "dietro-front", ma è solo questione di matematica....
Ecco la souzione quantificata.
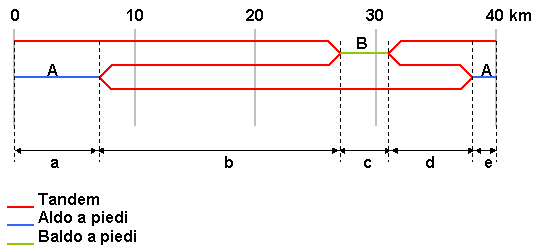
Il sistema risolvente è:
(indico con t il tempo necessario a compiere tutto il percorso e con a, b, c, d, e le lunghezze della varie tappe in cui è diviso il percorso come illustrato nella figura qui sopra.
Dopo alcune semplificazioni si ottiene:
La matrice del sistema è la seguente:
| a | b | c | d | e | t | = |
| 1 | 1 | 1 | 1 | 1 | 0 | 40 |
| 1 | 3 | 1 | 3 | 1 | -40 | 0 |
| 20 | 3 | 3 | 3 | 20 | -120 | 0 |
| 1 | 1 | 10 | 1 | 1 | -40 | 0 |
| 17 | -6 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | -6 | 17 | 0 | 0 |
| 0 | -2 | 9 | -2 | 0 | 0 | 0 |
Il sistema contiene 6 variabili e 7 equazioni, ma è di rango 5 perciò ha infinite soluzioni dipendenti da un parametro, indicato con k.
Per ogni soluzione possibile, tuttavia, il tempo è sempre lo stesso.
Ecco le soluzioni
La variabile a deve essere maggiore o uguale di zero, perciò:
0 <= e <= 2160/241
Casi particolari:
Il seguente grafico spazio-tempo inviato da Franco illustra chiaramente la possibilità di avere diverse soluzioni per questo problema.
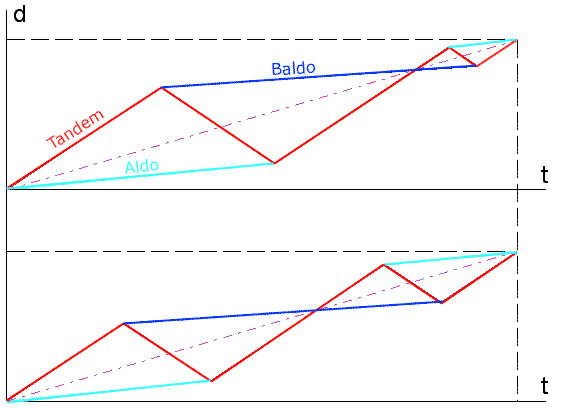
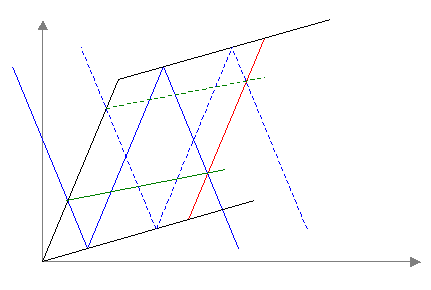
Franco dice: "Nella mia rappresentazione grafica in coordinate t e d (e stavolta in scala) ho disegnato in celeste il tragitto a piedi di Aldo, in blu quello di Baldo e in rosso quello del tandem: vengono fuori dei "romboidi" (non so definire una figura con due lati paralleli e due "quasi paralleli") con la diagonale maggiore (linea tratteggiata) sempre con la stessa inclinazione. E poichè tale inclinazione rappresenta la velocità media..."
Ecco un altro grafico (non in scala) che può essere utile per dare l'idea, dal punto di vista geometrico.
Facendo scorrere la linea spezzata blu e di conseguenza anche la linea verde, si ottiene un range di soluzioni comprese fra due limiti ben determinati.
Nella figura sono mostrate due soluzioni.
Una bicicletta per due
Due amici devono percorrere 30 km e hanno una sola bicicletta a
disposizione.
Come possono organizzarsi per arrivare a destinazione nel più breve tempo possibile?
xhtml 1.1
Sito Web realizzato da Gianfranco Bo