
[BASE Cinque - Appunti di Matematica ricreativa]
Storia, varianti e soluzioni di un racconto matematico.
In questi giorni mi sono finalmente deciso a ricostruire la storia del problema delle tre brocche.
La difficoltà principale è stata quella di trovare in rete gli Annales Stadenses dell'abate Alberto di Stade (1187-1260), scritti in latino, nei quali si trova la versione più antica di questo problema.

Alla fine li ho trovati ed è stata un bella emozione. Gli Annales Stadenses sono una cronaca universale dalla Creazione del mondo al 1256. La sorpresa è che a un certo punto c'è un dialogo tra due giovani litterati, curiales et curiosi di nome Tirri e Firri i quali si lanciano sfide matematiche. Il dialogo si svolge la vigilia di Natale del 1179, anno in cui morì Santa Ildegarda di Bingen.
Due importanti versioni successive del problema sono quelle di Luca Pacioli e di Nicolò Tartaglia.
Alcune versioni di Luca Pacioli si trovano nel libro De viribus quantitatis del 1508 e nel Codice Vaticano latino 3129 del 1478.
Quella di Nicolò Tartaglia si trova nel General Trattato de' numeri et misure del 1556.
> dMGH - digitalen Monumenta Germaniae Historica
Contiene gli Annales Stadenses. Link diretto: Annales Stadenses.
> BAV - Biblioteca Apostolica Vaticana
Contiene il Codice Vaticano latino 3129. Link diretto alla pagina dei Vaticani latini.
> Uriland, di Dario Uri
Contiene la copia manoscritta del De viribus quantitatis, codice 250 della Biblioteca Universitaria di Bologna. I fogli da consultare sono: 97, 98, 99 retto e verso.
Contiene il General Trattato de' numeri et misure. Consultare il libro 16, problema 132.
Qui riporto i problemi tradotti in un italiano abbastanza moderno. Per le versioni originali rimando alle fonti citate.
Mi è statoinoltre molto utile il libro: Dario Bressanini, Silvia Toniato, I giochi matematici di fra' Luca Pacioli. Trucchi, enigmi e passatempi di fine Quattrocento, Dedalo, 2011.
Dialogo di Tirri e Firri (Alberto di Stade , 1256)
Buon Firri, ti proporrò anch’io un problema, e certamente più sottile.
Il mio signore, che voleva dare un banchetto, mi ha mandato alla città vicina a prendere il vino. Ho portato con me un recipiente capace di 8 misure. Riempito quello, alla taverna non restava altro vino. Tornando a casa ti incontro e anche tu stai andando a prendere il vino.
Mi chiedi da dove arrivo e ti rispondo: "Dal foro, sto portando il vino al mio signore".
Mi chiedi quanto vino e ti rispondo: "Otto misure".
Tu mi dici: "Anch’io sto andando a prendere il vino."
Ti rispondo: "Non ne troverai."
Mi chiedi allora di dividere il mio vino con te.
Ti chiedo se hai dei recipienti. Mi dici di averne due, uno da 5 misure e l’altro da 3.
Ti darò la metà, e cioè 4 misure, se saprai dividere il vino con questi recipienti.
Dividilo, oppure resterai senza vino.
Firri tacque e non riuscì a fare la divisione.
Tirri disse: "Farò io la divisione, se non sei capace. Deponi i tuoi recipienti. "
Dividere a metà una botte di vino (Luca Pacioli, Vaticano latino 3129, 1478)
Due persone devono dividere il vino contenuto in una botte da 8 some in modo da averne 4 some ciascuno, e non hanno misure o strumenti di cui servirsi se non altre due botti vuote, una da 5 some e l’altra da 3.
Domando come fanno a dividerlo in due parti uguali.
Due altre sottili divisioni di botti (Luca Pacioli, De viribus quantitatis, 1508)
Un altro sottil caso sarebbe chi dicesse che una delle botti tenesse 10 some di vino e fosse piena e delle due vuote l'una tenesse 4 some l'altra 6 some.
Dividere il contenuto della botte piena fra due persone in modo che ciascuno abbia 5 some di vino.
E ancora a dire che la botte piena tiene 12 some e le due vuote tengono 4 e 8 some.
Dividere a metà il contenuto della botte piena.
Pacioli aggiunge che questi casi richiedono una speculazione più sottile e la soluzione è lasciata al lettore che certo la intenderà. E l'idiota a cui sia proposto questo problema si affaticherà invano, cercando l'impossibile.
I due ladri (Nicolò Tartaglia, General Trattato de' numeri et misure, 1556)
Due persone rubarono a un signore un'ampolla di balsamo che conteneva 8 once di balsamo.
Costoro, mentre si allontanavano, trovarono un vetraio che aveva soltanto due ampolle della capacità di 5 once e 3 once. Per la fretta che avevano, comprarono queste due ampolle e camminarono a lungo finché furono in un luogo sicuro. Poi si misero a dividere a metà il balsamo rubato.
Domando come fecero, non avendo nè pesi nè altra misura certa.
In questo caso, per curiosità, riporto il testo originale.
Sono duoi, che hanno robbato una ampoletta di balsamo a uno signor, nella qual era dentro oncie 8 di balsamo.
A ponto accadette che costoro nel suo partire trovorno uno vedriaro, che haveva solamente due ampolette l'una delle quali teneua oncie 5, l'altra oncie 3 e cosi per la pressa, che loro havevano egli comperorono queste 2 e caminorno di longo fin che furono al luogo sicuro, poi si misero a voler partir questo balsamo.
Dimando come fecero non havendo ne peso, ne altra misura certa.
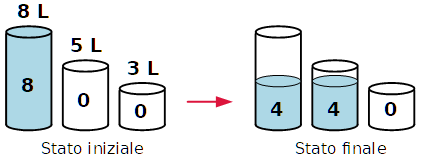
Partiamo dal caso classico, (8,5,3).
Hai tre recipienti, A, B, C della capacità di 8, 5, 3 litri.
Non sono graduati.
All'inizio il recipiente da 8 litri è pieno d'acqua mentre gli altri sono
vuoti.
Devi riuscire a dividere l'acqua in due parti uguali ottenendo 4 litri in A e 4
litri in B.
Puoi travasare dell'acqua da un recipiente ad un'altro quante volte vuoi.
Come fai?
Il problema si può risolvere per tentativi più o meno organizzati usando una tabella.
Ogni terna di numeri nella tabella rappresenta uno stato del sistema.
Si deve partire dallo stato (8,0,0) e arrivare allo stato (4, 4, 0).
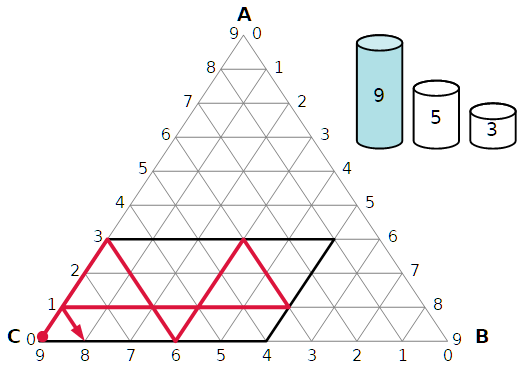
Ecco la soluzione data da Pacioli nel De viribus quantitatis.
| vaso
da 8 |
vaso
da 5 |
vaso
da 3 |
|
| stato iniziale | 8 | 0 | 0 |
| 1° travaso | 5 | 0 | 3 |
| 2° travaso | 5 | 3 | 0 |
| 3° travaso | 2 | 3 | 3 |
| 4° travaso | 2 | 5 | 1 |
| 5° travaso | 7 | 0 | 1 |
| 6° travaso | 7 | 1 | 0 |
| 7° travaso | 4 | 1 | 3 |
| stato finale | 4 | 4 | 0 |
Osserviamo che ad ogni travaso accade una delle seguenti cose (o entrambe).
Quindi in ogni stato possibile, c'è almeno un recipiente vuoto e/o un recipiente pieno.
La soluzione si può cercare anche usando un diagramma ternario.
Un diagramma ternario è una rappresentazione su un triangolo equilatero di un sistema costituito da 3 variabili la cui somma è costante.
Nel nostro caso:
Vediamo come funziona.
Osservate la figura.
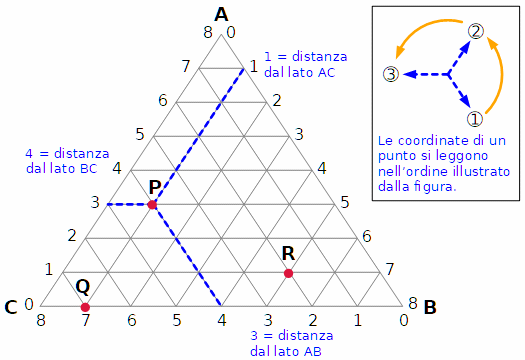
Le coordinate di P sono (4,1,3). Il punto P indica lo stato in cui i recipienti A, B, C contengono rispettivamente 4, 1, 3 litri.
Quali sono le coordinate di A, B, C, Q e R?
Risposte: Q(7,1,1), R(2,5,1), A(0,0,8), B(0,8,0), C(8,0,0).
Osservate la figura.
Costruiamo un diagramma ternario ABC di lato 8 = il contenuto della brocca piena.
Costruiamo il parallelogramma di lati:
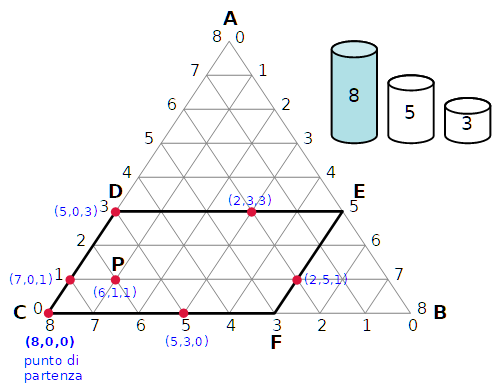
La prima cosa da capire è che tutti e soli gli stati raggiungibili si trovano sul contorno del parallelogrammo CDEF.
La dimostrazione è lasciata al lettore.
Qui osservo per esempio che lo stato P(6,1,1) non è raggiungibile perché non c'è né un recipiente vuoto né uno completamente pieno. E così accade per tutti i punti non appartenenti al contorno del parallelogrammo CDEF.
La seconda cosa da capire è che per trovare una sequenza di stati successivi si può immaginare di lanciare una pallina dalla posizione iniziale e farla rimbalzare sul contorno del parallelogrammo CDEF come se fosse una palla in un biliardo.
Qui sotto c'è un esempio.
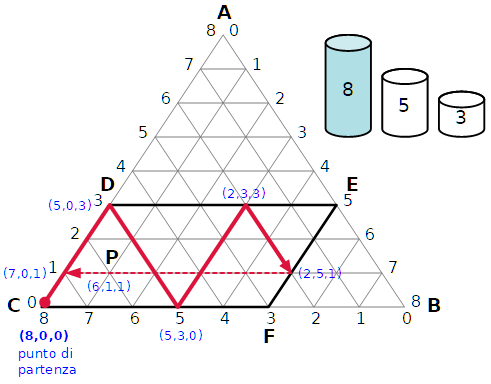
Si procede per tentativi, cercando di raggiungere lo stato finale.
Per esempio, qui sotto è rappresentata la soluzione data da Luca Pacioli e scritta nella tabella.
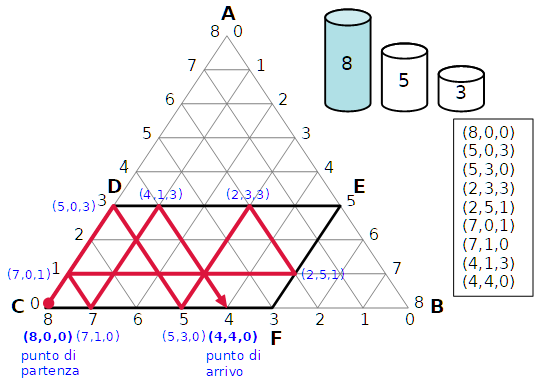
Possiamo chiederci se cè una soluzione con meno travasi.
Eccola.
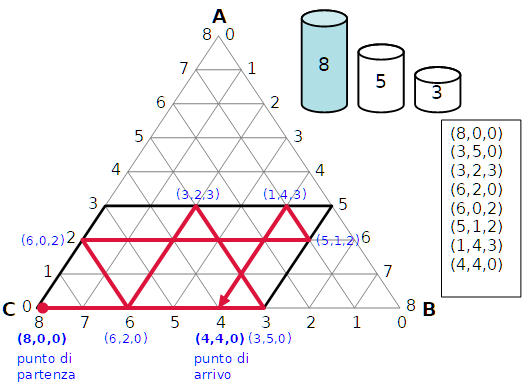
In questo caso le capacità dei tre recipienti sono rispettivamente 10, 6, 4 litri.
Bisogna dividere a metà i 10 litri, raggiungendo lo stato finale (5,5,0).
Pacioli dice che l'idiota a cui sia proposto questo problema si affaticherà invano, cercando l'impossibile.
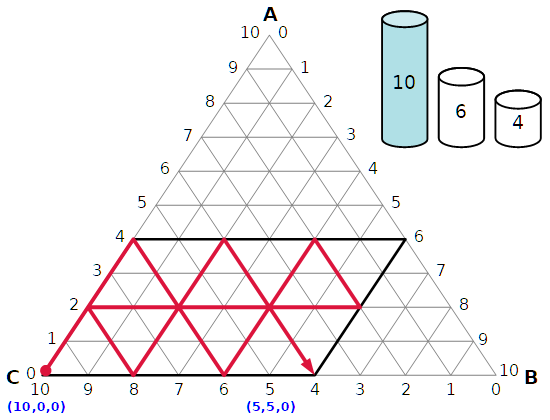
Invece la divisione sarebbe possibile se le capacità dei recipienti fossero 10, 7, 3 litri.
Ecco una soluzione in 10 travasi.
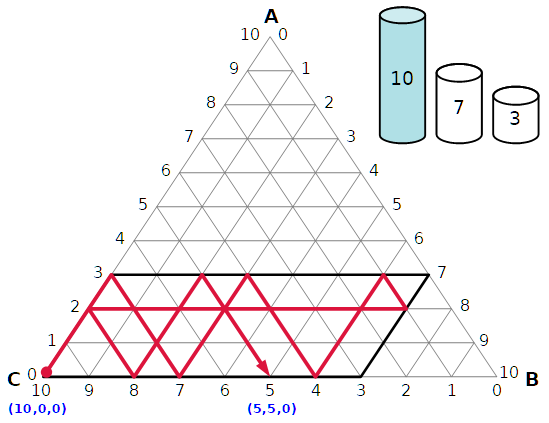
Da approfondire.
C'è una risposta semplice.
Siano a, b, c, sono le capacità delle tre brocche con:
Se a, b sono numeri primi fra loro allora si può dividere a metà la quantià di liquido a.
Da approfondire.
Nei casi i cui:
Figura non pertinente
---
Pace e bene a tutti.
GfBo
Data creazione: marzo 2020
Ultimo aggiornamento: marzo 2020
xhtml 1.1
Sito Web realizzato da Gianfranco Bo