[BASE Cinque - Appunti di Matematica ricreativa]
Sette domande matematiche sul racconto I sette messaggeri, di Dino Buzzati
![]() In fondo a
questa pagina trovate il racconto completo
In fondo a
questa pagina trovate il racconto completo![]()
Un principe parte dalla capitale per raggiungere i confini del regno di suo padre.
Porta con sé una scorta di fedeli cavalieri fra i quali sceglie sette messaggeri che facciano la spola tra lui e la capitale, per comunicare con i suoi cari.
Per distinguerli più facilmente impone loro nomi con le iniziali alfabeticamente progressive: Alessandro, Bartolomeo, Caio, Domenico, Ettore, Federico, Gregorio.
Con il passare dei giorni, dei mesi e degli anni la distanza si fa sempre più grande e le comunicazioni sempre piu rare...
In questo racconto, sebbene si parli di estensione di un regno, non troverete misure di lunghezza ma di tempo: giorni o anni di viaggio.
C'è un solo accenno, all'inizio, in cui il principe afferma che un giorno di viaggio equivale a quaranta leghe.
Domanda 1. Dopo quanti giorni, rispetto all'inizio del viaggio, Alessandro sarà di ritorno?
Domanda 2. Più in generale, se un messaggero parte il giorno n-esimo, in quale giorno sarà di ritorno?
Domanda 3. Dopo quanti giorni, rispetto all'inizio del viaggio, sarà di ritorno ciascuno di essi?
Domanda 4. La sequenza delle partenze si può esprimere con una formula matematica generale?
Domanda 5. La sequenza dei successivi intervalli fra un arrivo e l’altro dei messaggeri si può esprimere con una formula matematica generale?
Domanda 6. Nel racconto il principe dichiara di aver viaggiato ininterrottamente per otto anni, sei mesi e quindici giorni. Quante leghe ha percorso?
Domanda 7. Quante leghe hanno percorso complessivamente i 7 messaggeri?
Dopo quanti giorni, rispetto all'inizio del viaggio, Alessandro sarà di ritorno?
La situazione è illustrata nella figura seguente.
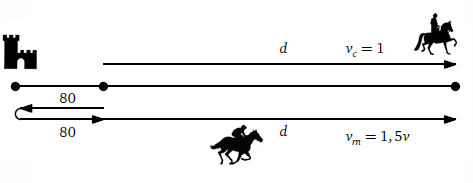
Ricordiamo le formule del moto rettilineo uniforme:
Il messaggero parte in un certo istante t0 in cui la carovana ha già percorso 80 leghe.
Il messaggero incontrerà nuovamente la carovana quando questa avrà percorso d leghe (incognita da trovare).
Assumiamo la velocità della carovana come unità di misura, così la velocità del messaggero è vm=1,5vc
La carovana percorre la distanza d nel tempo:
t = d/vc = d/1 = d
Il messaggero percorre la distanza 80 + 80 + d nello stesso tempo:
t = (160 + d)/vm = (160 + d)/1,5
Uguagliamo le due quantità, ottenendo così un'equazione nell'incognita d:
d = (160 + d)/1,5
Con qualche passaggio otteniamo:
0,5d = 160
Da cui si ricava:
d = 320 leghe
Ora possiamo ricavare il tempo, usando la velocità reale della carovana:
t = 320/40 = 8 giorni.
Dunque Alessandro sarà di ritorno 8 giorni dopo sua partenza ovvero 10 giorni dall'inizio del viaggio.
Il seguente grafico illustra i primi 27 giorni con i percorsi dei primi due messaggeri.
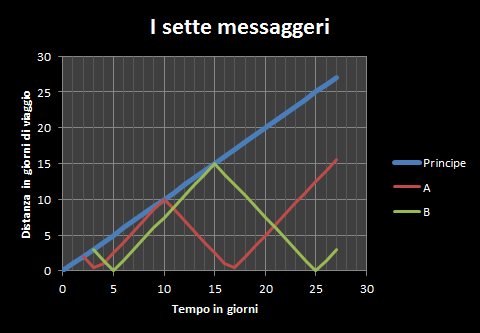
Nel prossimo grafico le distanze sono espresse in leghe anziché giorni di viaggio. Il grafico illustra un anno intero.
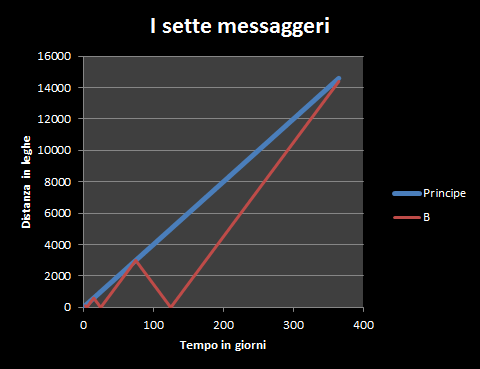
La stessa situazione rappresentata in coordinate polari.
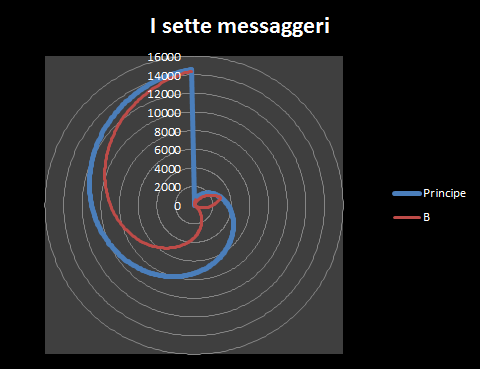
Più in generale, se un messaggero parte il giorno n, in quale giorno sarà di ritorno?
Riprendiamo il nostro disegno e usiamo una variabile per indicare il punto di partenza del messaggero.
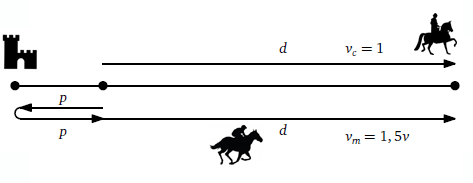
Il messaggero parte in un certo istante t0 in cui la carovana ha già percorso p leghe.
Il messaggero incontrerà nuovamente la carovana quando questa avrà percorso d leghe.
La carovana percorre la distanza d nel tempo:
t = d/vc = d/1
Il messaggero percorre la distanza p + p + d nello stesso tempo:
t = (2p + d)/vm = (2p + d)/1,5
Uguagliamo le due quantità, ottenendo così un'equazione nell'incognita d:
d = (2p + d)/1,5
Con qualche passaggio otteniamo:
0,5d = 2p
Da cui si ricava:
d = 4p
Significa che se un messaggero parte a una certa distanza dalla capitale, ritornerà quando la carovana avrà percorso quattro volte quella distanza. Cioè quando si troverà a cinque volte quella distanza.
E con i tempi?
Poiché la velocità è costante, quanto detto per gli spazi percorsi vale anche per i tempi.
Se un messaggero parte al tempo t (dal momento della partenza) ritornerà al tempo:
t+4t=5t.
Dopo quanti giorni, rispetto all'inizio del viaggio, sarà di ritorno ciascuno di essi?
A questo punto la risposta è facile, basta moltiplicare per 5 i tempi delle rispettive partenze.
| messaggero | giorno
partenza |
giorno
ritorno |
| Alessandro | 2 | 10 |
| Bartolomeo | 3 | 15 |
| Caio | 4 | 20 |
| Domenico | 5 | 25 |
| Ettore | 6 | 30 |
| Federico | 7 | 35 |
| Gregorio | 8 | 40 |
I primi 40 giorni per tutti i 7 messaggeri.
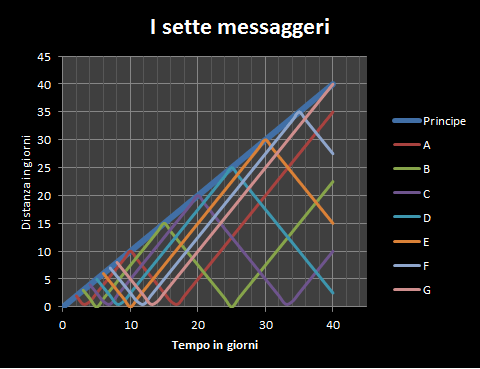
Stessa situazione in coordinate polari.
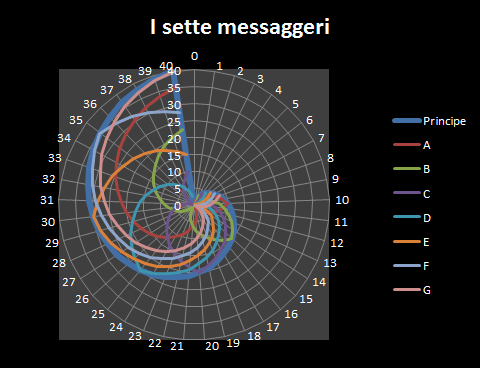
La sequenza delle partenze si può esprimere con una formula matematica generale?
Basta moltiplicare per 5 i successivi giorni di arrivo (che in pratica coincidono con quelli di partenza).
| messaggero | giorno
1° partenza |
giorno
2° partenza |
giorno
3° partenza |
giorno
n° partenza |
| Alessandro | 2 | 10 | 50 | 2·5n |
| Bartolomeo | 3 | 15 | 75 | 3·5n |
| Caio | 4 | 20 | 100 | 4·5n |
| Domenico | 5 | 25 | 125 | 5·5n |
| Ettore | 6 | 30 | 150 | 6·5n |
| Federico | 7 | 35 | 175 | 7·5n |
| Gregorio | 8 | 40 | 200 | 8·5n |
La sequenza dei successivi intervalli fra un arrivo e l’altro dei messaggeri si può esprimere con una formula matematica generale?
Nel racconto il principe dichiara di aver viaggiato ininterrottamente per otto anni, sei mesi e quindici giorni. Quante leghe ha percorso?
Questa è super-facile.
365 · 8 + 30 · 6 + 15 + 2 = 3117 giorni. (ci ho messo 2 anni bisestili, e ho conteggiato i 6 mesi da 30 giorni, ma la situazione è dubbia)
3117 · 40 = 124 680 leghe.
Il problema ora è: quanto è una lega? A seconda dei contesti è una misura di lunghezza che varia da 4 a 6 km.
Perciò la distanza percorsa dal principe e dalla sua carovana varia da 499 360 km a 749 040 km.
A titolo di informazione, vi segnalo che la circonferenza della Terra è circa 40 000 km.
Questo racconto è tutto il contrario del giro del mondo in 80 giorni!
Nota: nel racconto Buzzati dice che è appena arrivato Domenico. Secondo i calcoli, Domenico dovrebbe arrivare il giorno 3125. Il mistero si infittisce...
Quante leghe hanno percorso complessivamente i 7 messaggeri?
I messaggeri vanno avanti e indietro ma è come se viaggiassero continuamente a velocità costante per 8 anni, 6 mesi e x giorni. Bisogna tener conto che nei giorni iniziali hanno viaggiato alla stessa velocità della carovana.
| messaggero | giorni
da 40 leghe |
giorni da 60 leghe |
| Alessandro | 2 | 3115 |
| Bartolomeo | 3 | 3114 |
| Caio | 4 | 3113 |
| Domenico | 5 | 3112 |
| Ettore | 6 | 3111 |
| Federico | 7 | 3110 |
| Gregorio | 8 | 3109 |
| Totali | 35 | 21784 |
In tutto fanno:
35 · 40 + 21784 · 60 = 1 308 440 leghe.
Otto anni e mezzo di spola per tutti i 7 messaggeri.
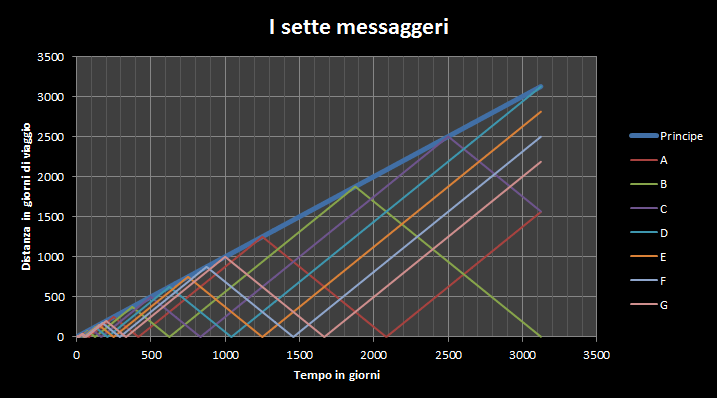
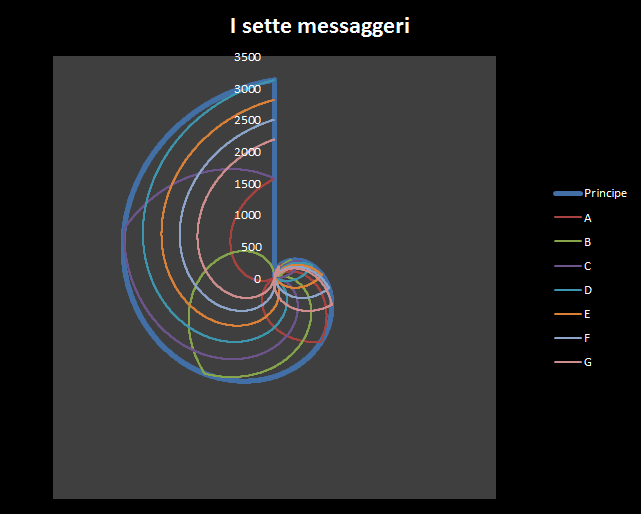
La stessa situazione in coordinate polari.
Partito ad esplorare il regno di mio padre, di giorno in giorno vado allontanandomi dalla città e le notizie che mi giungono si fanno sempre più rare. Ho cominciato il viaggio poco più che trentenne e più di otto anni sono passati, esattamente otto anni, sei mesi e quindici giorni di ininterrotto cammino. Credevo, alla partenza, che in poche settimane avrei facilmente raggiunto i confini del regno, invece ho continuato ad incontrare sempre nuove genti e paesi; e dovunque uomini che parlavano la mia stessa lingua, che dicevano di essere sudditi miei.
Penso talora che la bussola del mio geografo sia impazzita e che, credendo di procedere sempre verso il meridione, noi in realtà siamo forse andati girando su noi stessi, senza mai aumentare la distanza che ci separa dalla capitale; questo potrebbe spiegare il motivo per cui ancora non siamo giunti all’estrema frontiera.
Ma più sovente mi tormenta il dubbio che questo confine non esista, che il regno si estenda senza limite alcuno e che, per quanto io avanzi, mai potrò arrivare alla fine.
Mi misi in viaggio che avevo già più di trent’anni, troppo tardi forse. Gli amici, i familiari stessi, deridevano il mio progetto come inutile dispendio degli anni migliori della vita. Pochi in realtà dei miei fedeli acconsentirono a partire.
Sebbene spensierato - ben più di quanto sia ora! – mi preoccupai di poter comunicare, durante il viaggio, con i miei cari, e fra i cavalieri della scorta scelsi i sette migliori, che mi servissero da messaggeri.
Credevo, inconsapevole, che averne sette fosse addirittura un’esagerazione. Con l’andar del tempo mi accorsi al contrario che erano ridicolmente pochi; e si che nessuno di essi è mai caduto malato, né è incappato nei briganti, né ha sfiancato le cavalcature. Tutti e sette mi hanno servito con una tenacia e una devozione che difficilmente riuscirò mai a ricompensare.
Per distinguerli facilmente imposi loro nomi con le iniziali alfabeticamente progressive: Alessandro, Bartolomeo, Caio, Domenico, Ettore, Federico, Gregorio.
Non uso alla lontananza dalla mia casa, vi spedii il primo, Alessandro, fin dalla sera del mio secondo giorno di viaggio, quando avevamo percorso già un’ottantina di leghe.
La sera dopo, per assicurarmi la continuità delle comunicazioni, inviai il secondo, poi il terzo, poi il quarto, consecutivamente, fino all’ottava sera di viaggio, in cui partì Gregorio. Il primo non era ancora tornato.
Ci raggiunse la decima sera, mentre stavamo disponendo il campo per la notte, in una valle disabitata. Seppi da Alessandro che la sua rapidità era stata inferiore al previsto; avevo pensato che, procedendo isolato, in sella a un ottimo destriero, egli potesse percorrere, nel medesimo tempo, una distanza due volte la nostra; invece aveva potuto solamente una volta e mezza; in una giornata, mentre noi avanzavamo di quaranta leghe, lui ne divorava sessanta, ma non di più.
Così fu degli altri. Bartolomeo, partito per la città alla terza sera di viaggio, ci raggiunse alla quindicesima; Caio, partito alla quarta, alla ventesima solo fu di ritorno. Ben presto constatai che bastava moltiplicare per cinque i giorni fin lì impiegati per sapere quando il messaggero ci avrebbe ripresi.
Allontanandoci sempre più dalla capitale, l’itinerario dei messi si faceva ogni volta più lungo. Dopo cinquanta giorni di cammino, l’intervallo fra un arrivo e l’altro dei messaggeri cominciò a spaziarsi sensibilmente; mentre prima me ne vedevo arrivare al campo uno ogni cinque giorni, questo intervallo divenne di venticinque; la voce della mia città diveniva in tal modo sempre più fioca; intere settimane passavano senza che io ne avessi alcuna notizia.
Trascorsi che furono sei mesi - già avevamo varcato i monti Fasani - l’intervallo fra un arrivo e l’altro dei messaggeri aumentò a ben quattro mesi. Essi mi recavano oramai notizie lontane; le buste mi giungevano gualcite, talora con macchie di umido per le notti trascorse all’addiaccio da chi me le portava.
Procedemmo ancora. Invano cercavo di persuadermi che le nuvole trascorrenti sopra di me fossero uguali a quelle della mia fanciullezza, che il cielo della città lontana non fosse diverso dalla cupola azzurra che mi sovrastava, che l’aria fosse la stessa, uguale il soffio del vento, identiche le voci degli uccelli. Le nuvole, il cielo, l’aria, i venti, gli uccelli, mi apparivano in verità cose nuove e diverse; e io mi sentivo straniero.
Avanti, avanti! Vagabondi incontrati per le pianure mi dicevano che i confini non erano lontani. Io incitavo i miei uomini a non posare, spegnevo gli accenti scoraggiati che si facevano sulle loro labbra. Erano già passati quattro anni dalla mia partenza; che lunga fatica. La capitale, la mia casa, mio padre, si erano fatti stranamente remoti, quasi non ci credevo. Ben venti mesi di silenzio e di solitudine intercorrevano ora fra le successive comparse dei messaggeri. Mi portavano curiose lettere ingiallite dal tempo, e in esse trovavo nomi dimenticati, modi di dire a me insoliti, sentimenti che non riuscivo a capire. Il mattino successivo, dopo una sola notte di riposo, mentre noi ci rimettevamo in cammino il messo ripartiva nella direzione opposta, recando alla città le lettere che da parecchio tempo io avevo apprestate.
Ma otto anni e mezzo sono trascorsi. Stasera cenavo da solo nella mia tenda quando è entrato Domenico, che riusciva ancora a sorridere benché stravolto dalla fatica. Da quasi sette anni non lo rivedevo. Per tutto questo periodo lunghissimo egli non aveva fatto che correre, attraverso praterie, boschi e deserti, cambiando chissà quante volte cavalcatura, per portarmi quel pacco di buste che finora non ho avuto voglia di aprire. Egli è già andato a dormire e ripartirà domani stesso all’alba.
Ripartirà per l’ultima volta. Sul taccuino ho calcolato che, se tutto andrà bene, io continuando il cammino come ho fatto finora e lui il suo, non potrò rivedere Domenico che fra trentaquattro anni. Io allora ne avrò settantadue. Ma comincio a sentirmi stanco ed è probabile che la morte mi coglierà prima. Così non lo potrò mai più rivedere.
Fra trentaquattro anni (prima anzi, molto prima) Domenico scorgerà inaspettatamente i fuochi del mio accampamento e si domanderà perché mai nel frattempo, io abbia fatto così poco cammino. Come stasera. il buon messaggero entrerà nella mia tenda con le lettere ingiallite dagli anni, cariche di assurde notizie di un tempo già sepolto; ma si fermerà sulla soglia, vedendomi immobile disteso sul giaciglio, due soldati ai fianchi con letorce, morto.
Eppure, va, Domenico, e non dirmi che sono crudele! Porta, il mio ultimo saluto alla città dove io sono nato. Tu sei il superstite legame con il mondo che un tempo fu anche mio. I più recenti messaggi mi hanno fatto sapere che molte cose sono cambiate, che mio padre è morto che la Corona è passata a mio fratello maggiore, che mi considerano perduto, che hanno costruito alti palazzi di pietra là dove prima erano le querce sotto cui andavo solitamente a giocare. Ma è pur sempre la mia vecchia patria.
Tu sei l’ultimo legame con loro, Domenico. Il quinto messaggero, Ettore, che mi raggiungerà, Dio volendo, fra un anno e otto mesi, non potrà ripartire perché non farebbe più in tempo a tornare. Dopo di te il silenzio, o Domenico, a meno che finalmente io non trovi i sospirati confini. Ma quanto più procedo, più vado convincendomi che non esiste frontiera.
Non esiste, io sospetto, frontiera, almeno non nel senso che noi siamo abituati a pensare. Non ci sono muraglie di separazione, né valli divisorie, né montagne che chiudano il passo. Probabilmente varcherò il limite senza accorgermene neppure, e continuerò ad andare avanti, ignaro.
Per questo io intendo che Ettore e gli altri messi dopo di lui, quando mi avranno nuovamente raggiunto, non riprendano più la via della capitale ma partano innanzi a precedermi, affinché io possa sapere in antecedenza ciò che mi attende.
Un’ansia inconsueta da qualche tempo si accende in me alla sera, e non è più rimpianto delle gioie lasciate, come accadeva nei primi tempi del viaggio; piuttosto è l’impazienza di conoscere le terre ignote a cui mi dirigo.
Vado notando - e non l’ho confidato finora a nessuno - vado notando come di giorno in giorno, man mano che avanzo verso l’improbabile mèta, nel cielo irraggi una luce insolita quale mai mi è apparsa, neppure nei sogni; e come le piante, i monti, i fiumi che attraversiamo, sembrino fatti di una essenza diversa da quella nostrana e l’aria rechi presagi che non so dire.
Una speranza nuova mi trarrà domattina ancora più avanti, verso quelle montagne inesplorate che le ombre della notte stanno occultando. Ancora una volta io leverò il campo, mentre Domenico scomparirà all’orizzonte dalla parte opposta, per recare alla città lontanissima l’inutile mio messaggio.
Tratto da: Dino Buzzati, La boutique del mistero (prima edizione Oscar Mondadori), Milano, 1968
Data creazione: luglio 2013
Ultimo aggiornamento: luglio 2013
xhtml 1.1
Sito Web realizzato da Gianfranco Bo