[HOME - BASE Cinque - Appunti di Matematica ricreativa]

Il problema originale di Collatz

Dalle note di Lothar Collatz del 1 luglio 1932

questa pagina contiene codice javascript
può essere scaricata ed eseguita senza essere collegati ad internet

Il problema originale di Collatz
Sembra che fra le note di Collatz datate 1 luglio 1932 si trovi questo problema:

Se n è un multiplo di 3, lo si moltiplichi per 2 e si divida il risultato per 3.
Se n/3 dà come resto 1, lo si moltiplichi per 4, si tolga 1 e si divida il risultato per 3.
Se n/3 dà come resto 2, lo si moltiplichi per 4, si aggiunga 1 e si divida il risultato per 3.

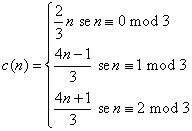
La domanda è: applicando ripetutamente la funzione c(n) a partire da un numero intero positivo, la sequenza che si ottiene diverge?, converge su un numero? diventa ciclica?

L'algoritmo di Collatz in javascript

Codice javascript di Gianfranco Bo

Si verifica facilmente che per gli interi 1,2,3,4,5,6,7 e 9 le sequenze entrano in un ciclo del tipo: 4,5,7,9,6.

Purtroppo non si sa ancora come va a finire la sequenza che parte dal numero 8!
Ecco i suoi primi 50 termini: 8, 11, 15, 10, 13, 17, 23, 31, 41, 55, 73, 97, 129, 86, 115, 153, 102, 68, 91, 121, 161, 215, 287, 383, 511, 681, 454, 605, 807, 538, 717, 478, 637, 849, 566, 755, 1007, 1343, 1791, 1194, 796, 1061, 1415, 1887, 1258, 1677, 1118, 1491, 994, 1325, 1767, ...

Risposte & riflessioni

Sito Web realizzato da Gianfranco Bo - (2003)