
[HOME - BASE Cinque - Appunti di Matematica ricreativa]
Quattro misteriose carte forate permettono di indovinare automaticamente un numero compreso fra 0 e 15, pensato da una persona onesta. Come funzionano? Dov'è il trucco?
Ci sono carte da gioco matematiche che sembrano compiere meraviglie.
Come si preparano le carte
Tagliate quattro carte quadrate, ognuna con lato di 8 centimetri
circa.
Lasciate intorno un margine di un centimetro e dividete lo spazio
rimasto in quadrati di un centimetro di lato.
Scrivete i numeri nelle caselle, come indicato nelle figure a fianco.
Attenti a non sbagliare!
Scrivete i "sì" e i "no" nei luoghi indicati e ritagliate i quadrati
o i rettangoli grigi segnalati con la lettera "R".
Notate che la carta 4 ha i numeri scritti davanti e dietro.

Come si gioca
Adesso che le carte sono pronte chiedete a qualcuno di pensare un
numero da 0 a 15. Mostrategli la faccia di ciascuna carta e
domandategli se il numero pensato è su quella carta. Se dice "sì"
mettete la carta sul tavolo con la parola "sì" in alto. Se dice "no"
giratela in modo che il "no" sia in alto.
Poi mettete le carte una sull'altra; per ultima quella che non ha
ritagli, la quale rimarrà sopra a tutte.
Voltate allora il mazzetto: il numero pensato apparirà attraverso un
foro quadrato.
Tratto e adattato da Irving Adler, Matematica, Mondadori, 1961.
Ogni domanda ci permette di dividere l'intervallo a metà. Perciò, se l'intervallo è n, il numero minimo di domande è log2 k, dovek è la più piccola potenza di 2 maggiore di n.
Nota storica
La prima versione di un gioco di divinazione binaria si trova in
Pacioli, De Viribus Quantitatis, c1500, Prob. 69: A trovare una moneta
fra 16 pensata. Pacioli risolve il gioco spostando le monete con un
procedimento un po' macchinoso e spiegato in modo non del tutto chiaro.
Per quel che riguarda le carte forate, riporto questa indicazione di David
Singmaster.
Martin Hansen. Mind probe. MiS 21:1 (Jan 1992) cover & 2-6. Adapts
binary divination to locate a number among 1 - 80 with four cards but each
card has its numbers half in black and half in white. Describes how to make 4
x 4 and 8 x 8 binary cards with holes so the chosen number will appear in the
hole. Adapts to ternary to produce triangular cards with holes so that the
chosen number appears in the hole. Hansen has kindly given me a set of these:
'The Kingswood Mathemagic Club's Window Cards'. He also describes 'logic
cards' which display the truth values of three basic quantities which are
consistent with various statements _ these were previously described by
Gardner and Cundy & Rollett.
Potete fotocopiare e ritagliare le seguenti carte che sono equivalenti a quelle proposte all'inizio. E' meglio fotocopiarle su un cartoncino leggero.
|
|
|
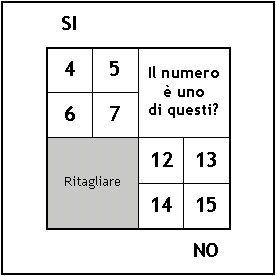
Carta 3
|
|
|
Divinazione binaria (appunti rapidi)
Il gioco sarebbe troppo scoperto se fosse fatto così.
Pensa un numero. (supponiamo che sia 4 oppure 5)
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
Bianco o grigio? Grigio.
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
Bianco o grigio? Grigio.
4 |
5 |
6 |
7 |
Bianco o grigio? Grigio.
4 |
5 |
Bianco o grigio?
Bianco = 4
Grigio = 5
La seguente disposizione permette di capire meglio perché determinati numeri sono scritti sulle carte.
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
Con la numerazione in base 2 tutto è più chiaro!
Se scriviamo i numeri in base 2 scopriamo che ogni domanda chiede un bit del numero pensato.
La carta 4 equivale alla domanda: “È maggiore di 7?”, cioè chiede il primo bit
| 0 | 0000 | 4 | 0100 | 8 | 1000 | 12 | 1100 |
| 1 | 0001 | 5 | 0101 | 9 | 1001 | 13 | 1101 |
| 2 | 0010 | 6 | 0110 | 10 | 1010 | 14 | 1110 |
| 3 | 0011 | 7 | 0111 | 11 | 1011 | 15 | 1111 |
La carta 3 equivale alla domanda: “È uno fra 4; 5; 6; 7; 12; 13; 14; 15?”, cioè chiede il secondo bit
| 0 | 0000 | 4 | 0100 | 8 | 1000 | 12 | 1100 |
| 1 | 0001 | 5 | 0101 | 9 | 1001 | 13 | 1101 |
| 2 | 0010 | 6 | 0110 | 10 | 1010 | 14 | 1110 |
| 3 | 0011 | 7 | 0111 | 11 | 1011 | 15 | 1111 |
La carta 2 equivale alla domanda: “È uno fra 2; 3; 6; 7; 10; 11; 14; 15?”, cioè chiede il terzo bit
| 0 | 0000 | 4 | 0100 | 8 | 1000 | 12 | 1100 |
| 1 | 0001 | 5 | 0101 | 9 | 1001 | 13 | 1101 |
| 2 | 0010 | 6 | 0110 | 10 | 1010 | 14 | 1110 |
| 3 | 0011 | 7 | 0111 | 11 | 1011 | 15 | 1111 |
La carta 1 equivale alla domanda: “È dispari?”, cioè chiede il quarto bit
| 0 | 0000 | 4 | 0100 | 8 | 1000 | 12 | 1100 |
| 1 | 0001 | 5 | 0101 | 9 | 1001 | 13 | 1101 |
| 2 | 0010 | 6 | 0110 | 10 | 1010 | 14 | 1110 |
| 3 | 0011 | 7 | 0111 | 11 | 1011 | 15 | 1111 |
Più in generale, come si può indovinare un numero pensato, in un certo intervallo, facendo il numero minimo di domande che abbiano risposte del tipo sì/no?
Ogni domanda ci permette di dividere l'intervallo a metà.
Perciò, se l'intervallo è n, il numero minimo di domande è:
log2
k
dove k è la più piccola potenza di 2 maggiore di n.
Data creazione: ottobre 2004
Ultimo aggiornamento: aprile 2006
html 4.01
Sito Web realizzato da Gianfranco Bo