[BASE Cinque - Appunti di Matematica ricreativa]

Quando si comincia dal fondo

Ovvero: i problemi del gambero

1. La scimmia e le noci di cocco

Una scimmia, durante una tempesta in mare, salvò la vita ad un marinaio.
Il marinaio, le promise eterna riconoscenza e, tanto per cominciare le regalò un sacco pieno di noci di cocco.
Durante la notte, però, il marinaio ci ripensò e decise di riprendersi qualche noce di cocco.

Il marinaio, dopo aver compiuto queste imprese, si ritirò nella sua cabina e dormì il sonno del giusto fino all'alba.
Fu svegliato dalle urla della scimmia.
Essa, anche se non sapeva contare, si era accorta del furto. Infatti nel sacco era rimasta una sola noce di cocco!
Quante noci conteneva il sacco, all'inizio?
(Il capostipite di questo problema si trova probabilmente nel papiro di Rhind, -1650. Altre versioni molto antiche sono dovute a Chiu Chang Suan Ching -150 ed a Mahavira, 850)

2. La calcolatrice di Sofia

La calcolatrice di Sofia è alquanto strana. Essa possiede tre tasti speciali:
a) un tasto C che capovolge il numero scritto sul visore;
b) un altro tasto T che lo triplica, cioè lo moltiplica per 3;
c) un terzo tasto M che lo dimezza.
Ad esempio, se sul visore sta scritto 258 e noi premiamo T otterremo 774. Se poi premiamo C otterremo 477. Se infine premiamo M otterremo 238,5.
Supponiamo che sul visore sia scritto 93.
Che numero otterremo se premiamo prima T, poi ancora T, poi C e poi M?

3. Sofia alle prese con la sua calcolatrice

Sofia ha digitato un numero sulla sua calcolatrice poi ha premuto la seguente sequenza di tasti: M, C, T. Sul visore compare il risultato: 111.
Quale numero aveva digitato Sofia?

4. Il castigo di San Gennaro

Un alcolista molto fedele a San Gennaro si accorge di essere a corto di soldi.

5. A vendere mezzo uovo

Quanti soldi c'erano nel portafogli all'inizio?

Una donna porta delle uova al mercato.

Così ha venduto tutte le uova che possedeva.
Quante uova possedeva?
Questo problema è quasi identico al a quello della scimmia e delle noci di cocco ma è un po' più sconcertante per il fatto delle mezze uova. Va precisato infatti che la donna ha venduto uova fresche e non uova sode.
(Giuseppe Peano 1925)

5. Le albicocche

Proposto da Ivana Niccolai
Un giovane entrò in un orto, in cui c'erano tre giardini e prese tante albicocche; per uscirne, dovette darne al primo guardiano la metà più 3, al secondo guardiano la metà di quelle che gli rimanevano più tre e poi al terzo guardiano la metà di quelle rimaste più tre: Riuscì così a conservare per sé solo un'albicocca.

Quante ne aveva raccolte?

6. Problema di 1° grado

Proposto da Ivana Niccolai
In una partita un giocatore perde 5/9 di quanto ha, nella seconda partita raddoppia la somma rimastagli, nella terza perde ancora i 2/11 di questa somma e rimane così con 72 euro.
Qual era la somma iniziale?

7. La Torre 2°

proposto da Pasquale
In una classe di un quinto Liceo Scientifico l'insegnante di matematica dettò il seguente problema ai propri allievi, tutti bravissimi e da sempre studenti modello:

"In una torre a forma di parallelepipedo il volume è pari a 180 metri cubi e la somma di uno dei lati della base con l'altezza è uguale all'incirca all'età di ciascuno di voi, ovviamente espressa in metri. Calcolare l'area della base della torre."

Dopo circa due ore, nessuno aveva ancora consegnato il compito, quando l'insegnante disse ai ragazzi:

"Dovete scusarmi, ma stamattina ero sovrappensiero, perché stavo pensando che ieri sera a casa mia, a tavola, abbiamo corso un brutto rischio ... sapete che sono molto superstizioso, ma per fortuna poi abbiamo rimediato ... Comunque, bando alle chiacchiere, vedendo che, stranamente, nessuno di voi ha risolto il compito ho notato che avevo dimenticato di dirvi che la semisomma dell'altezza della torre con uno dei lati della base è uguale al numero delle mele che mia moglie ha comprato ieri al mercato."

Infatti, con quest'ultimo dato, di lì a poco, tutti consegnarono il compito con la soluzione esatta: quale?

8. Zero e uno in cerchio

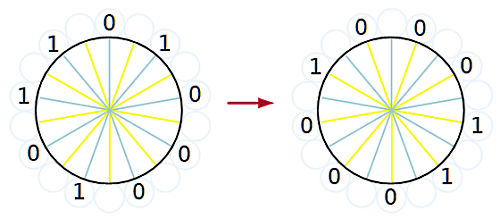
Scrivete quattro 1 e cinque 0 in cerchio, in ordine casuale.

Poi applicate la seguente regola:

  1. Tra due numeri uguali scrivete un 1 e tra due numeri diversi scrivete uno 0.
  2. Poi cancellate i numeri originali.

Potete applicare nuovamente la regola, quante volte volete.

Per esempio nella figura, a sinistra, vedete una possibile distribuzione iniziale di 1 e 0. A destra, invece, ciò che si ottiene applicando la regola una volta.

Cerchio 0 1

Domanda: è possibile ottenere tutti 1 applicando la regola un numero finito di volte?

---

Tratto da: Strategies of problem solving (Draft) di Maria Nogin, 2008.

Questo problema è citato anche nel libro The Mathematics of Various Entertaining Subjects, Volume 3 -  The Magic of Mathematics, a cura di Jennifer Beineke e Jason Rosenhouse, 2019.

Risposte & riflessioni

1. La scimmia e le noci di cocco
All'inizio c'erano 15 noci di cocco. Il marinaio ne ha preso successivamente 8, 4, 2.
E' facile risolvere i problemi di questo tipo se si parte dal fondo...

2. La calcolatrice di Sofia
369

3. Sofia alle prese con la sua calcolatrice
111-37, 37-73, 73-146

4. Il castigo di San Gennaro

La sequenza diretta è: 2625x2-3000=2250 -> 2250x2-3000=1500 -> 1500x2-3000=0
Perciò all'inizio nel portafogli c'erano 2625 Lire.

5. A vendere mezzo uovo
Ringrazio Marta Sartori che ha segnalato un errore e la soluzione esatta.
7 uova.
Per risolverlo partiamo dal fondo.

5. Le albicocche
La risposta è 50 albicocche.

Risposta inviata da Ivana Niccolai
Indico con x il numero delle albicocche raccolte in tutto; il primo guardiano ne riceve x/2 +3

Ne rimangono, quindi, x/2 , 3

Imposto l'equazione:

(((x/2 , 3 ) /2 , 3 )/2 , 3) = 1

(((x , 18)/4)/2 , 3 ) = 1

(x , 18 ,24 )/8 = 1

x , 18 , 24 = 8

x = 18 + 24 +8

x = 50

Il problema può essere risolto anche facendo un semplice ragionamento a ritroso: se alla fine gli è rimasta una sola albicocca significa che, prima di pagare l'ultimo pedaggio al terzo guardiano, aveva 8 albicocche; infatti la metà di 8 è 4 e togliendo a 4 tre albicocche rimane una sola albicocca.

Prima del secondo pedaggio aveva 22 albicocche; infatti la metà di 22 è 11 e togliendo a 11 tre albicocche restano proprio 8 albicocche.

Prima del primo pedaggio aveva esattamente 50 albicocche; infatti la metà di 50 è 25 e togliendo a 25 tre albicocche restano proprio 22 albicocche.

Pertanto in ogni passaggio a ritroso occorre aggiungere 3 al numero delle albicocche rimastee raddoppiare il numero ottenuto; infatti:
(1 + 3 ) * 2 = 8;
(8 +3) *2 = 22;
(22 + 3) * 2 = 50

6. Problema di 1° grado
Quanto ha: x
Prima partita: x - 5x/9
Seconda partita: 2(x - 5x/9)
Terza partita: 2(x - 5x/9) - 2(2(x - 5x/9))/11
Equazione:
2(x - 5x/9) - 2(2(x - 5x/9))/11 = 72
Risolviamola per passi, procedendo a ritroso:
(9/11)(2(x - 5x/9)) = 72
2(x - 5x/9) = 88
(x - 5x/9) = 44
(4/9)x = 44
x = 99.

7. La torre 2°
L'area di base della torre risulta essere pari a dieci metri quadrati.

Considerando, infatti, intere tutte le misure della torre, dell'età media degli alunni ed il numero delle mele acquistate al mercato il giorno precedente dalla moglie del professore, altrimenti sarebbe impossibile impostare un procedimento analitico se comprendiamo l'infinità di numeri decimali o anche irrazionali, partiamo dall'unico dato preciso del problema, che nel caso specifico è il volume della torre, pari a 180 metri cubi, e scomponiamolo subito in fattori primi:

180 = 2²·3²·5

Per rispondere al quesito è necessario ora produrre tutte le possibili terne di numeri interi, rappresentative delle tre dimensioni del parallelepipedo rettangolo, che, moltiplicati tra loro, producono 180 metri cubi di volume. Dobbiamo considerare, però, che uno dei tre spigoli, od al massimo anche due di essi, potrebbe anche essere di lunghezza unitaria e quindi le terne possibili salgono alle seguenti 20:

180·1·1
90·2·1
60·3·1
45·4·1
45·2·2
36·5·1
30·6·1
30·3·2
20·9·1
20·3·3
18·10·1
18·5·2
15·12·1
15·6·2
15·4·3
12·5·3
10·6·3
10·9·2
9·5·4
6·6·5

Ognuna di esse sarebbe potuta essere la soluzione giusta senza gli altri dati forniti dall'insegnante. Onde sfoltire tale lista occorre allora tener conto anche di questi ultimi, seppur incerti, controllando quali possibili terne possono rientrare nei limiti imposti. Esaminiamo dapprima il dato iniziale che la somma di uno dei lati della base del parallelepipedo con l'altezza è uguale all'incirca all'età di ciascun alunno espressa in metri, tenendo conto che per ciascuna terna di numeri interi su scritti non sappiamo quali sono le due misure che rientrano fra i lati di base, ovvero in ogni terna qualsiasi dimensione può essere rappresentativa dell'altezza del parallelepipedo e quindi tutte le terne individuano tre possibili sottocasi, e che i ragazzi, che stanno risolvendo il problema, conoscono benissimo la media della loro età, ovvero è per essi un dato noto, certamente inconfutabile.

Riguardo alla prima considerazione possiamo però asserire che il parallelepipedo rettangolo da individuare deve avere l'aspetto caratteristico di una torre e che in queste normalmente la dimensione dell'altezza è sempre notevolmente maggiore rispetto ai lati della base, mentre questi ultimi possono essere o meno paragonabili tra loro. Ciò implica che in ciascuna terna possiamo considerare valido solo uno dei suddetti tre sottocasi, e precisamente quello che associa ai lati della base le due misure più piccole, ed inoltre che bisogna escludere le terne 15·12·1, 10·9·2 e 6·6·5 le quali darebbero origine a parallelepipedi le cui altezze risulterebbero paragonabili ad almeno uno dei due lati della base.

Riguardo alla seconda considerazione, invece, possiamo dire che gli studenti, frequentando il quinto Liceo Scientifico, hanno un'età media che può, al massimo, variare dai 17 ai 19 anni, non tenendo presente cioè la possibilità di numerosissimi eventuali ripetenti presenti nella classe visto che nelle premesse del testo del problema si dice esplicitamente che gli alunni sono tutti bravissimi e da sempre studenti modello.

Alla luce di quanto stabilito possiamo dire che nella terna 180·1·1 la misura 180 metri corrisponderebbe all'altezza della torre, che sommata ad uno dei lati della base darebbe un'età media degli alunni di 181 anni il che è umanamente impossibile! Escludiamo anche la terna 90·2·1 che fornirebbe invece un'età media superiore a quella di pensionamento per vecchiaia (ben oltre i 90 anni), e, per lo stesso motivo, eliminiamo ancora le terne 60·3·1, 45·4·1, 45·2·2, 36·5·1, 30·6·1, 30·3·2, 20·9·1, 20·3·3 e 18·5·2 in quanto in ogni caso darebbero sempre alunni troppo anziani o comunque con un'età superiore ai prestabiliti 19 anni. Possiamo, per finire, escludere anche le terne 10·6·3 e 9·5·4 visto che darebbero invece un'età media degli allievi al di sotto dei prefissati 17 anni. Restano così ammissibili le seguenti quattro terne sulle quali tutti gli alunni non possono far altro che indugiare a lungo senza consegnare il compito in quanto tutte equiprobabili:

18·10·1
15·6·2
15·4·3
12·5·3

Se ne deduce che l'età media degli alunni risulta pari o a 17 anni (= 15 + 2 = 12 + 5), oppure 18 anni (= 15 + 3), od infine 19 anni (= 18 + 1 = 15 + 4). Poichè 18 anni si ottiene in modo univoco possiamo scartare a questo punto anche l'eventualità che a tale valore corrisponde l'età media degli studenti: se così fosse, infatti, essi non avrebbero bisogno di un'ulteriore informazione per risolvere il quesito in quanto l'unica terna che produce appunto tale media è 15·4·3. Non possiamo estromettere però la stessa terna in quanto essa produce anche una media pari ai 19 anni di età che si ottiene, come visto, in duplice modo. I ragazzi hanno pertanto o 17 o 19 anni ed hanno bisogno necessariamente di altri dati per poter risolvere il problema. Il professore aggiunge con ritardo che la semisomma dell'altezza della torre con uno dei lati della base è uguale al numero delle mele che sua moglie ha comprato al mercato il giorno precedente. I risultati di tale calcolo producono per la terna 18·10·1:

(18 + 10)/2 = 28/2 = 14
(18 + 1)/2 = 19/2 = 9,5

quest'ultimo impossibile perchè non intero; per la terna 15·6·2 invece producono:

(15 + 6)/2 = 21/2 = 10,5
(15 + 2)/2 = 17/2 = 8,5

entrambi impossibili; per la terna 15·4·3 invece producono:

(15 + 4)/2 = 19/2 = 9,5
(15 + 3)/2 = 18/2 = 9

il primo impossibile, il secondo accettabile; infine per la terna 12·5·3 risulta:

(12 + 5)/2 = 17/2 = 8,5
(12 + 3)/2 = 15/2 = 7,5

nuovamente entrambi impossibili. Restano pertanto in gioco le terne 18·10·1 e 15·4·3 a cui corrisponde un'età media per gli studenti di 19 anni e da cui si ricavano rispettivamente 14 e nove mele acquistate al mercato dalla moglie del professore il giorno prima; considerando almeno una mela per ciascun commensale, quanti potevano essere seduti a tavola a casa del docente? Poiché siamo in Italia e quest'ultimo è molto superstizioso, altro dato del problema, bisogna dedurre che inizialmente erano in tutto 13, ospiti compresi, e già questo converge sulle 14 mele, ma se consideriamo che in questi casi, i "molto superstiziosi" usano tenersi un invitato di riserva (un vero amico o un parente) da aggiungere a tavola (salvo che all'ultimo momento qualcuno degli invitati non declini il suo invito), in questo caso i commensali erano proprio 14. D'altra parte il professore afferma anche che era riuscito a rimediare alla scaramanzia (altro dato). Dunque l'unica terna resta 18·10·1 da cui si ricava un'area di base della torre di esattamente 10·1 = 10 metri quadrati.

8. Zero e uno in cerchio

...

---

Pace e bene a tutti.

GfBo

Data creazione: 2005

Ultimo aggiornamento: agosto 2020

html5

Sito Web realizzato da Gianfranco Bo