[BASE Cinque - Appunti di Matematica ricreativa]

La divisibilità per 7 è una passeggiata in un grafo

Tutti noi a scuola abbiamo imparato i criteri di divisibilità per i numeri 2, 3, 4, 5, 6, 8, 9, 10.

Perché il 7 manca all'appello?

Forse perché il criterio di divisibilità per 7 è più macchinoso della divisione stessa. Perciò, per scoprire se un numero è divisibile per 7, conviene eseguire la divisione e verificare se il resto viene 0.

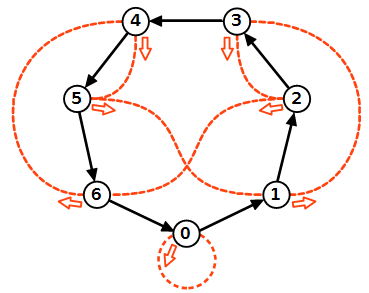
Tuttavia esiste un criterio di divisibilità per 7 che è davvero facile come una passeggiata e persino divertente. Infatti è proprio una passeggiata in questo grafo che vi permetterà di sapere il resto della divisione di qualunque numero naturale per 7 senza eseguire la divisione e usando soltanto le cifre del numero stesso.

Come si usa?

Considerate per esempio il numero 654.

---

1) 654 è formato dalle cifre 6, 5, 4.

2) Partite dal nodo 0 del grafo.

3) Seguite 6 frecce nere in successione e poi una freccia arancione (arrivate sul 4).

4) Proseguite con 5 frecce nere e una freccia arancione. (arrivate sul 6)

5) Proseguite con 4 frecce nere (arrivate sul 3).

6) Il numero del grafo su cui siete arrivati a fine percorso è il resto della divisione: 654 : 7 = 93 con resto 3.

7) Se finite sullo 0 allora il numero di partenza è divisibile per 7.

---

In generale

Dato qualunque numero n, quanto fa n MOD 7?

1. Scrivete un numero N.
2. Partite dal nodo 0 del grafo.
3. Per ogni cifra C di N, seguite C frecce nere in successione e, prima di passare alla cifra successiva, seguite una freccia arancione.
4. Ricordate che dopo l'ultima cifra, quella delle unità, non dovete seguire una freccia arancione.
5. Il numero del grafo su arrivate a fine percorso è il resto della divisione di N per 7.
6. Se il percorso termina sullo 0, allora N è divisibile per 7.

Perché funziona?

Nel grafo:

• i nodi numerati da 0 a 6 rappresentano i possibili resti della divisione dei numeri naturali per 7;
• gli archi orientati con freccia nera rappresentano l'operazione +1 (addizione di una unità) MODULO 7
• gli archi orientati con freccia arancione rappresentano l'operazione ×10 (moltiplicazione per 10) MODULO 7

La via più lunga

Supponiamo di usare soltanto questo grafo per trovare il resto della divisione di un numero n per 7, cioè n MOD 7

In questo grafo ogni freccia nera rappresenta l'operazione +1.

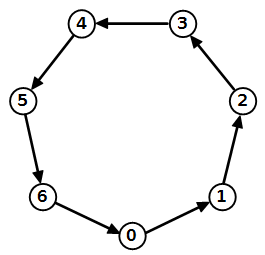
Supponiamo di voler calcolare, per esempio:

23 MOD 7 = 2

23 = 1+1+1+1+1+1+1+1+1+1+... (23 volte).

Dobbiamo partire dallo 0 e seguire 23 frecce nere. Arriviamo al numero 2. Tre giri completi più due passi. Abbastanza veloce.

Ma se volessimo calcolare:

654 MOD 7 = 3

dovremmo partire dallo 0 e seguire 654 frecce nere. Sarebbero 93 giri completi più 3 passi. Troppo lungo!

Gli archi di colore arancione sfruttano la rappresentazione decimale dei numeri per abbreviare il percorso.

Salti nell'iperspazio

Mi piace pensare agli archi arancione come a salti nell'iperspazio numerico che permettono di saltare con un solo passo da un numero a un'altro numero 10 volte più grande, sempre MODULO 7.

Come si trovano questi salti?

Semplice, basta compilare la tabella dei multipli di 10 MOD 7.

Cosa vi dice la tabella?

Sapendo n MOD 7, la tabella vi dice quanto è (n×10) MOD 7.

Per esempio, sapendo che 396 MOD 7 = 4 vi dice che 3960 MOD 7 = 5.

Dalla tabella si ricavano i seguenti collegamenti (salti nell'iperspazio):

0 con 0, 1 con 3, 2 con 6, 3 con 2, 4 con 5, 5 con 1, 6 con 4.

Eccoli disegnati sul grafo.

Rappresentazione dei numeri naturali con le operazioni +1 e ×10

Come sfruttare al meglio i salti nell'iperspazio numerico MOD 7?

Ogni numero naturale si può scrivere usando soltanto l'addizione di una unità (+1) e la moltiplicazione per 10 (×10).

Per esempio:

654 = ((1+1+1+1+1+1)×10+1+1+1+1+1)×10+1+1+1+1

Attenzione alle parentesi!

Ovvero, usando gli stessi colori del grafo:

654 = ((1+1+1+1+1+1)×10+1+1+1+1+1)×10+1+1+1+1

Verifichiamo:

654 = (60+1+1+1+1+1)×10+1+1+1+1

654 = (65)×10+1+1+1+1

654 = 650+1+1+1+1

654 = 654

Ovvero, sul grafo MOD 7:

654 = 6 frecce nere + salto + 5 frecce nere + salto + 4 frecce nere.

Tre modi di disegnare il grafo

Disegno 1. I nodi con i resti della divisione per 7 sono disposti in cerchi. Gli archi arancione sono disegnati in modo da evidenziare le simmetrie.

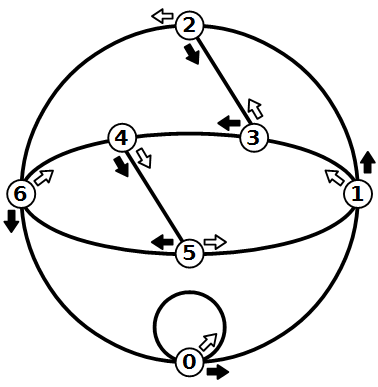
Disegno 2. Il grafo è disegnato senza incroci fra gli archi, per evidenziare che è un grafo piano. Le frecce sono nere e bianche. Credit David Wilson (dal blog di Tanya Khovanova)

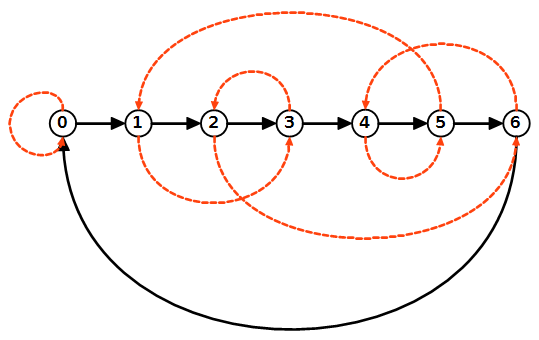
Disegno 3. Il grafo è disegnato in forma lineare. Si nota facilmente che esiste un percorso arancione che passa per tutti i nodi maggiori di 0.

Il bello

Il bello è che per ogni numero naturale esiste un grafo di questo tipo!

E che i grafi dei numeri da 2 a 13 si possono costruire in pochi minuti!

Ma questa è un'altra storia...

.

Pace e bene a tutti!

Gianfranco Bo

Data creazione: giugno 2015

Ultimo aggiornamento: giugno 2015

xhtml 1.1

Sito Web realizzato da Gianfranco Bo