[BASE Cinque - Appunti di Matematica ricreativa]

Una sequenza di Nob Yoshigahara

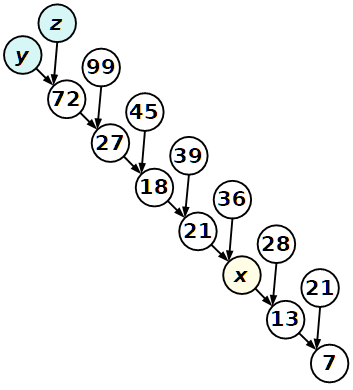
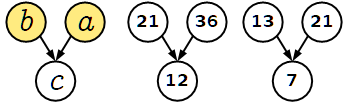
I numeri nei cerchi bianchi sono scritti seguendo una certa regola.

a) Scoprite la regola e scrivete il valore di x.

b) Meditate sulla psico-logica con cui è stato scritto questo gioco e scrivete i valori di y e z.

c) Potete pure scrivere un programma per trovare i numeri y e z.

Nota storica.

E' l'espansione di un problema di Nobuyuki Yoshigahara pubblicato sul suo libro Puzzles 101: A PuzzleMasters Challenge , CRC Press, 2004 .

Nob scrive nel libro: "As maker of tricky puzzles, I consider this my masterpiece."

"Come creatore di enigmi complicati, considero questo il mio capolavoro."

Risposte & riflessioni

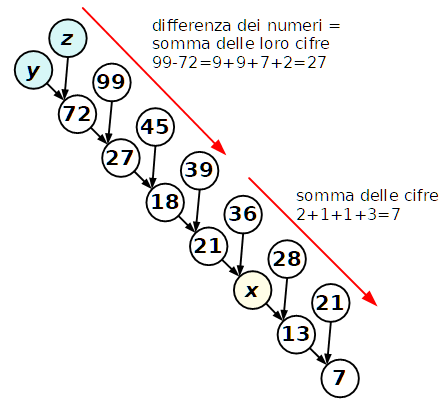
A una prima osservazione, si nota che i numeri 72, 27, 18, 21 sono la differenza dei due numeri a cui sono collegati con le frecce.

99 - 72 = 27, 45 - 27 = 18, ..., 36 - 21 = 15(?)

Ma subito ci accorgiamo che l'operazione non funziona con la terna 21, 13, 7.

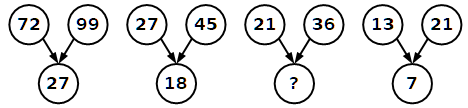
Qual è allora la regola?

Dopo qualche ragionamento, scopriamo che ogni numero su cui arrivano due frecce è la somma delle cifre dei due numeri ad esso collegati.

9 + 9 + 7 + 2 = 27, ..., 1 + 3 + 2 + 1 = 7

Quindi:

x = 2 + 1 + 3 + 6 = 12

La cosa interessante...

...di questo problema è che, partendo dall'alto, all'inizio la sequenza segue una regola "forte", poi tale regola si "indebolisce". Tutta la sequenza però segue anche la regola "debole".

La regola "forte"

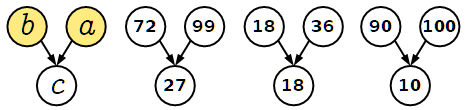
Tre numeri, a, b, c, formano una terna quando si verificano le due condizioni:

• c = a - b
• c = somma delle cifre di a, b

La regola "debole"

Tre numeri, a, b, c, formano una terna quando si verifica la condizione:

• c = somma delle cifre di a, b

Nobuyuki è stato bravo a trovare le terne (99, 72, 27), (45, 27, 18), (39, 18, 21) che sono dominabili a occhio.

Come continua la sequenza verso l'alto?

A questo punto possiamo chiederci come continua la sequenza verso l'alto, seguendo la regola "forte".

Bisogna trovare (i più piccoli) due numeri tali che:

• la loro differenza sia 72
• la somma delle loro cifre sia 72

I numeri sono: 39969 e 39897.

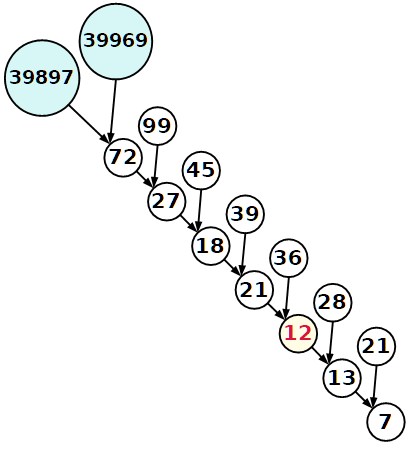
Si può procedere all'infinito, ma i numeri diventano sempre più enormi!

Un programmino per trovare i numeri

Per velocizzare il programma si possono sfruttare le seguenti proprietà:

1. b deve essere un multiplo di 9
2. a deve essere uguale a b + 72, quindi si fa il test solo sulla somma delle cifre.

Se invece vogliamo cercare tutte le terne, i tempi di ricerca si allungano notevolmente.

---

DECLARE EXTERNAL FUNCTION sommacifre
LET massimo=10^5
FOR b=0 TO massimo STEP 9
   LET a=b+72
   LET sa=sommacifre(a)
   LET sb=sommacifre(b) 
   LET d=a-b
   IF d=sa+sb THEN PRINT a;b;d
NEXT b
PRINT "Fine"
END

EXTERNAL FUNCTION sommacifre(n)
LET n$=STR$(n)
LET l=LEN(n$)
LET sommac=0
FOR i = 1 TO l
   LET sommac=sommac+VAL(n$(i:i))
NEXT i
LET sommacifre=sommac
END FUNCTION

---

La funzione sommacifre(n) converte il numero n in una stringa da cui estrae i caratteri uno alla volta.

Si possono anche estrarre le singole cifre di un numero usando soltanto operazioni matematiche.

---

Pace e bene a tutti.

Data creazione: febbraio 2020

Ultimo aggiornamento: febbraio 2020

xhtml 1.1

Sito Web realizzato da Gianfranco Bo