 Il percorso magico ottenuto seguendo l'ordine dei numeri |
 Il percorso magico ottenuto collegando ordinatamente e separatamente i numeri pari (linea arancione) e i numeri dispari (linea azzurra) |
[HOME - BASE Cinque - Appunti di Matematica ricreativa]
Che cosa è un quadrato magico? E un quadrato semi-magico? Un piccolo
pro-memoria.
In generale un quadrato magico si costruisce disponendo tutti i numeri interi da
1 a n2 in una griglia di n*n caselle in modo tale che la somma dei
numeri di ogni riga, di ogni colonna e di ogni diagonale sia sempre la stessa.
Il numero di righe (e di colonne) si chiama ordine del quadrato, mentre
la somma di una riga (o colonna o diagonale) si chiama costante magica.
| 2 | 7 | 6 |
| 9 | 5 | 1 |
| 4 | 3 | 8 |
Quello dell'esempio è un quadrato magico di ordine 3 e la sua costante
magica è 15.
Un quadrato è detto semi-magico se sono uguali soltanto i totali delle
righe e delle colonne.
I percorsi magici
Se si collegano i centri delle caselle di un quadrato magico in un certo
ordine, si possono ottenere delle figure interessanti.
Partiamo, ad esempio da questo quadrato più-che magico
|
1 |
15 |
14 |
4 |
|
12 |
6 |
7 |
9 |
|
8 |
10 |
11 |
5 |
|
13 |
3 |
2 |
16 |
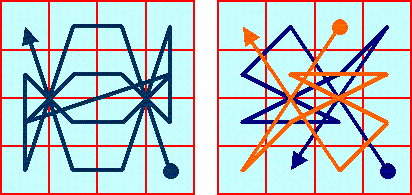
 Il percorso magico ottenuto seguendo l'ordine dei numeri |
 Il percorso magico ottenuto collegando ordinatamente e separatamente i numeri pari (linea arancione) e i numeri dispari (linea azzurra) |
Il quadrato magico della Melancolia di Albrecht Durer (1514)
|
16 |
3 |
2 |
13 |
|
5 |
10 |
11 |
8 |
|
9 |
6 |
7 |
12 |
|
4 |
15 |
14 |
1 |
I percorsi magici di Claude Bragdon
I percorsi magici sono stati utilizzati dall'architetto statunitense Claude
Bragdon (1866-1946) per costruire decorazioni artistiche.
L'esempio seguente è basato su un quadrato semi-magico.
|
 N.B. Alla fine del percorso, il punto 16 è stato unito con il punto 1 |
Figure tratte da una tavola di C. Bragdon intitolata
"A 4x4 square, its magic path and various derived patterns".
The Architectural Forum, v.26, (1917)
(febbraio 2004)
Sito Web realizzato da Gianfranco Bo