(x + yi)2 = 5 + 12i
x2 − y2 + 2xyi = 5 + 12i
x2 − y2 = 5
2xy = 12
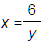
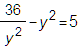
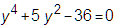
[x=−2i, y=3i], [x=2i, y=−3i], [x=−3, y=−2], [x=3, y=2]
(3 + 2i), (−3 − 2i)
In conclusione:
√(5 + 12i) = ±(3 + 2i)
[BASE Cinque - Appunti di Matematica ricreativa]
Quali sono le radici quadrate di 5+12i?
Più avanti c'è un breve ripasso. Qui c'è la soluzione.
Il metodo applicato a questo esempio si può applicare in ogni caso.
Nei numeri complessi come anche in quelli reali, vale la seguente:
Definizione. Una radice quadrata di un numero complesso a + bi è un numero complesso x + yi che elevato al quadrato dà come risultato a + bi.
(x + yi)2 = a + bi
---
Troviamo le radici quadrate di 5 + 12i
(x + yi)2 = 5 + 12i
x2 − y2 + 2xyi = 5 + 12i
x2 − y2 = 5
2xy = 12
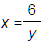
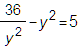
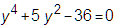
[x=−2i, y=3i], [x=2i, y=−3i], [x=−3, y=−2], [x=3, y=2]
(3 + 2i), (−3 − 2i)
In conclusione:
√(5 + 12i) = ±(3 + 2i)
Ogni numero complesso diverso da 0 ha due radici quadrate.
Definizione. Una radice quadrata di un numero reale n è un numero x che elevato al quadrato dà come risultato n.
x2 = n
Troviamo la (o le) radici quadrate di 25.
Chiediamoci: quale (o quali) numeri reali elevati al quadrato danno come risultato 25?
E' facile trovare due numeri, 5 e −5, infatti:
52 = 25
(−5)2 = 25
Le due radici di un numero reale positivo n sono due numeri opposti e si indicano:
√n, −√n
Tornando all'esempio:
√25 = 5, −√25 = −5
Si può anche scrivere:
±√25 = ±5
Attenzione: √25 = ±5 è una scrittura sbagliata perché √25 indica la sola radice positiva.
La radice di un numero negativo non esiste nei numeri reali.
√−25 = ?
Non esiste un numero reale x tale che:
x2 = −25
Se vogliamo dare un valore alle radici quadrate dei numei negativi è sufficiente che diciamo qual è la radice quadrata di −1.
√−1 = i
Con la lettera i si indica l'unità immaginaria.
Allora possiamo scrivere, per esempio:
√−25 = √25 · √−1 = 5·i = 5i
C'e anche l'altra soluzione:
−√−25 = −√25 · √−1 = −5 · i = −5i
Usando la definizione di i si ottiene:
i = √−1
i2 = −1
i3 = i2 · i = −i
i4 = i2 · i2 = 1
i5 = i4 · i = i
e così via...
Ma anche:
i−1 = 1 / i = i / i2 = −i
i−2 = i / i3 = −1
e così via...
---
Salvo errori e omissioni
---
Pace e bene a tutti.
Data creazione: febbraio 2020
Ultimo aggiornamento: febbraio 2020
xhtml 1.1
Sito Web realizzato da Gianfranco Bo