[BASE Cinque - Appunti di Matematica ricreativa]

Trasferimento di palline

Grazie a Giampiero Nardone per aver inviato il seguente problema al Forum di BASE Cinque.

Trasferimento di palline

Mettiamo in una scatola 13 palline bianche e 15 nere.

Abbiamo anche fuori dalla scatola 28 palline nere a disposizione.

Togliamo due palline dalla scatola.

• Se hanno colori diversi, rimettiamo la pallina bianca nella scatola. L'altra pallina la gettiamo via.
• Se hanno lo stesso colore, le gettiamo via e mettiamo una pallina nera nella scatola.

Continuiamo, fino a quando rimane una sola pallina nella scatola. Qual è il suo colore?

Altre domande:

In quanti passaggi si completa l'opera?

Qual è l'albero delle possibilità?

Trasferimento di palline - generalizzazione

Generalizzare il precedente problema al caso di (n,m) palline, rispettivamente bianche-nere.

Data creazione: maggio 2007

Ultimo aggiornamento: maggio 2007

Risposte & riflessioni

Trasferimento di palline

Risposta secca: l'ultima pallina che rimane nella scatola è bianca.

Spiegazione inviata da Jepa.
Mmmm , secondo me essendo le biglie bianche 13 e potendo togliere le biglie bianche per forza due alla volta, cioè quando prelevi 2 biglie bianche e di conseguenza ne metti dentro una nera, alla fine rimane dentro la scatola una biglia bianca e un numero imprecisato di biglie nere variabile statisticamente. A quel punto giungerai dopo un certo numero di prelievi ad avere per forza una sola biglia bianca ed una sola nera. Pertanto rimane nella scatola la biglia bianca!!

Risposta secca: l'opera si completa in 27 passaggi.

Spiegazione inviata da Enrico Delfini.
La mia domanda sulla "diversità" non voleva fare riferimento allo sbilanciamento cromatico, ma alla molteplicità degli stati posssibili.

• Al tempo zero: abbiamo una configurazione possibile
• al tempo 1 , ne abbiamo tre............
• .........
• .....al tempo 25, abbiamo due sondizioni possibili
• al tempo 26, c'è solo una possibilità
• idem al 27esimo step

Se scrivessimo in un foglio, ad ogni rigo, la serie delle possibili distribuzioni, quanto deve essere largo il foglio? A che altezza?

Spiegazione inviata da Gianfranco Bo

Per costruire l'albero delle possibilità ho fatto le seguenti considerazioni:

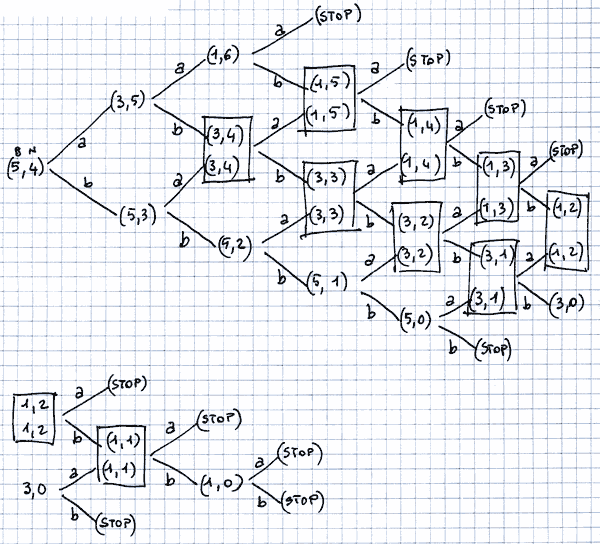
a) partiamo, ad esempio, da una situazione iniziale (5B, 4N) e disegniamo il grafo delle possibili evoluzioni;

b) a ogni mossa il grafo si dirama (al max) in due vie nel modo seguente:

• - caso a): se pesco BB allora nella scatola le bianche diminuiscono di 2 e le nere aumentano di 1 (-2B+1N)
• - caso b) se pesco NN oppure BN allora nella scatola le bianche rimangono come sono e le nere diminuiscono di 1 (-1N);

c) nella seguente figura si vede lo sviluppo del grafo in grande.

d) nella seguente figura si vede il grafo completo in piccolo.

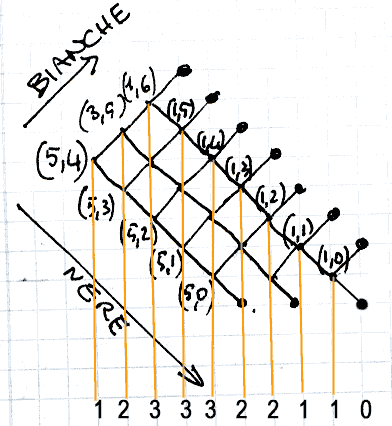
In questo esempio la sequenza dei casi possibili è:

1,2,3,3,3,2,2,1,1,0

e il gioco si risolve al max alla ottava mossa.

Analizzando lo schema, si scopre che può essere generalizzato al caso di (n,m) biglie.

Nella seguente figura, inviata da Panurgo, ad esempio è tracciato lo schema per (13,15)

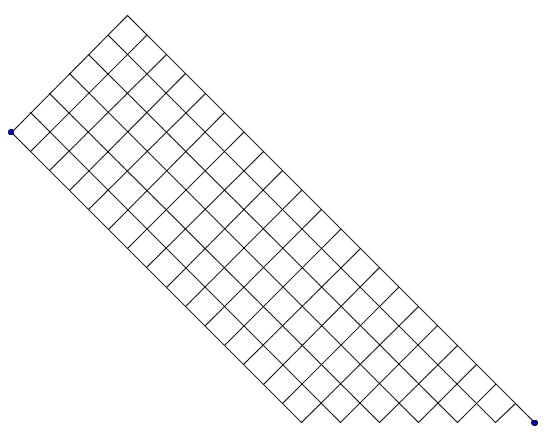
La sequenza dei casi possibili è:

1,2,3,4,5,6,7,7,7,7,7,7,7,7,7,6,6,5,5,4,4,3,3,2,2,1,1,0

Trasferimento di palline - generalizzazione

Bisogna meditare ancora un po'...

xhtml 1.1

Sito Web realizzato da Gianfranco Bo