[BASE Cinque - Appunti di Matematica ricreativa]

I 15 migliori trucchi di calcolo mentale

Sarebbe meglio chiamarli "tecniche" e non "trucchi"

perché la matematica talvolta è magica, ma senza alcun inganno

Cose da sapere 1: conoscere bene il nostro sistema di numerazione posizionale in base 10

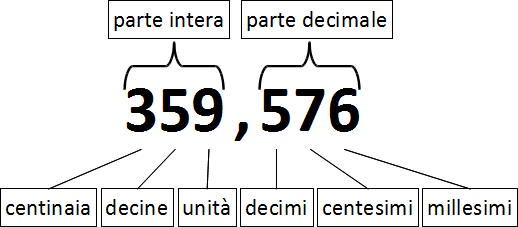
Nella scrittura di un numero decimale si distinguono due parti: la parte intera, che è quella prima della virgola e la parte decimale che è quella dopo la virgola.

Ciascuna cifra ha un valore che dipende dalla posizione che essa occupa nel numero stesso.

Tale valore si chiama valore posizionale della cifra.

Procedendo da destra verso sinistra, il valore posizionale delle cifre aumenta di 10 volte per ogni posto (o ordine).

Il nostro sistema posizionale è detto in base 10 perché ci vogliono 10 unità di un posto (o ordine) per formare 1 unità del posto superiore.

Esempi.

10 unità = 1 decina

10 decine = 1 centinaio

10 centinaia = 1 migliaio

Grazie a questo sistema, possiamo scrivere ogni numero come una somma di centinaia, decine, unità, decimi, e così via.

Questa scrittura si chiama forma polinomiale del numero. Il termine deriva da polinomio che significa molti nomi.

Esempi.

35 = 30 + 5 = (3 × 10) + (5 × 1)

872 = 800 + 70 + 2 = (8 × 100) + (7 × 10) + (2 × 1)

2054 = 2000 + 50 + 4 = (2 × 1000) + (5 × 10) + (4 × 1)

La forma polinomiale di un numero sembra complicata ma in realtà può semplificare notevolmente i calcoli.

Cose da sapere 2: conoscere perfettamente le tabelline della moltiplicazione da 1×1 a 9×9

Non basta. Bisogna anche sapere perfettamente:

• le tabelline dell'addizione da 1+1 a 9+9;
• le potenze di 2 da 2⁰ a 2¹⁰;
• le potenze di 3 da 3⁰ a 3⁵
• i quadrati dei numeri da 1 a 20;
• i cubi dei numeri da 1 a 10;
• i numeri primi da 2 a 53;

Per allenarti su questi punti puoi usare A.N.GE.LO., l'Allenatore Numerico Generale e Loquace.

Ecco qui un schema delle potenze e dei numeri primi.

Potenze di 2

Potenze di 3

Quadrati e cubi

Numeri primi da 2 a 53

2 - 3 - 5 - 7 - 11 - 13 - 17 - 19 - 23 - 29 - 31 - 37 - 41 - 43 - 47 - 53

I numeri primi da 2 a 53 sono soltanto 16.

Cose da sapere 3: conoscere bene alcune proprietà delle operazioni

Le tecniche di calcolo mentale rapido usano alcune proprietà delle operazioni.

Le principali sono: commutativa, associativa (e dissociativa), distributiva.

• Proprietà commutativa di + e × (addizione e moltiplicazione)
  3 + 2 = 2 + 3
  3 × 2 = 2 × 3
  Cambiando l'ordine degli addendi (o dei fattori) il risultato non cambia.
  
• Proprietà associativa di + e × (addizione e moltiplicazione)
  2 + 3 + 4 = (2 + 3) + 4 = 2 + (3 + 4) = 5 + 4 = 2 + 7
  2 × 3 × 4 = (2 × 3) × 4 = 2 × (3 × 4) = 6 × 4 = 2 × 12
  In un'addizione (o moltiplicazione) di 3 o più termini, se al posto di alcuni termini si sostituisce la loro somma (o prodotto) il risultato non cambia.
• La proprietà associativa si può applicare anche "alla rovescia" e in questo caso si chiama dissociativa.
  15 + 21 = 10 + 5 + 20 + 1

  3 × 14 = 3 × (10 + 4)

  In un calcolo, al posto di un numero se ne possono sostituire due o più che combinati assieme diano come risultato il numero sostituito.

• Proprietà distributiva di × rispetto a + (moltiplicazione rispetto all'addizione)
  2 × (3 + 4) = (2 × 3) + (2 × 4)
  5 × (2 + 3 + 4) = 5 × 2 + 5 × 3 + 5 × 4
  Per moltiplicare un numero per un'addizione di due o più numeri si può moltiplicare il numero stesso per ciascuno degli addendi e addizionare i prodotti parziali ottenuti.

Tecnica n. 1: addizionare o sottrarre usando pacchetti di 10, 100, ...

Per addizionare (o sottrarre) due numeri si parte dal più grande e si aggiunge (o sottrae) il più piccolo dopo averlo scomposto in decine più un eventuale resto in unità.

Esempi.

23 + 12 = 23 + 10 + 2 = 35

35 + 42 = 42 + 30 + 5 = 77

94 - 52 = 94 - 50 - 2 = 42

658 - 12 = 658 - 10 - 2 = 646

Se il numero più piccolo è di 3 cifre, lo si scompone in centinaia, ed eventualmente in decine e in unità.

Esempi.

547 + 235 = 547 + 100 + 100 + 10 + 10 + 10 + 5 = 782

798 - 301 = 798 - 300 - 1 = 497

Tecnica n. 2: moltiplicare o dividere un numero per 10, per 100, per 1000, ...

Per moltiplicare un numero intero per 10, oppure per 100, oppure per 1000 basta aggiungere alla sua destra rispettivamente 1, oppure 2, oppure 3 zeri.
Se il numero è decimale, allora si sposta la virgola di 1, oppure 2, oppure 3 posti verso destra.

Esempi.

35 × 10 = 350

74 × 100 = 7400

5,83 × 10 = 58, 3

27,32 × 1000 = 27.320

Per dividere un numero intero per 10, oppure per 100, oppure per 1000 basta eliminare alla sua destra rispettivamente 1, oppure 2, oppure 3 zeri.
E se non ci sono zeri? In tal caso si sposta la virgola rispettivamente di 1 oppure 2 oppure tre posti verso destra.

Esempi.

350 : 10 = 35

297 : 100 = 2,97

4 : 10 = 0,4

Tecnica n. 3: moltiplicare o dividere un numero per 2, il doppio, la metà

Per calcolare la metà di un numero si può fare la metà delle unità, delle decine, delle centinaia, ... che lo compongono e addizionare i risultati ottenuti.

Esempi.

46 : 2 = 40 : 2 + 6 : 2 = 20 + 3 = 23

58 : 2 = 50 : 2 + 8 : 2 = 25 + 4 = 29

Per calcolare il doppio di un numero si può fare il doppio delle unità, delle decine, delle centinaia, ... che lo compongono e addizionare i risultati ottenuti.

Esempi.

34 × 2 = 30 × 2 + 4 × 2 = 60 + 8 = 68

237 × 2 = 200 × 2 + 30 × 2 + 7 × 2 = 400 + 60 + 14 = 474

Tecnica n. 4: moltiplicare un numero per 1,5

Nota che 1,5 = uno e mezzo.

Per moltiplicare un numero per 1,5 si può aggiungere al numero stesso la sua metà.
Oppure si può calcolare la sua metà e moltiplicarla per 3.

Esempi.

18 × 1,5 = 18 + 9 = 27

84 × 1,5 = 84 + 42 = 126

5 × 1,5 = 5 + 2,5 = 7,5

Tecnica n. 5: moltiplicare un numero per 4, per 8

Nota che 4 è il doppio di 2

Per moltiplicare un numero per 4 basta moltiplicarlo due volte per 2 ovvero fare il doppio del doppio del numero stesso.

Esempi.

18 × 4 = 18 × 2 × 2 = 36 × 2 = 72

53 × 4 = 106 × 2 = 212

35 × 4 = 140

Questa tecnica si può estendere alla moltiplicazione per 8, che è uguale a 2 × 2 × 2.

Per moltiplicare un numero per 8 basta moltiplicarlo tre volte per 2 ovvero calcolare il doppio del doppio del doppio del numero stesso.

Esempio.

31 × 8 = 31 × 2 × 2 × 2 = 248

Tecnica n. 6: dividere un numero per 4

Per dividere un numero per 4 basta dividerlo due volte per 2 ovvero fare la metà della metà del numero stesso.

Esempi.

84 : 4 = 84 : 2 : 2 = 42 : 2 = 21

124 : 4 = 62 : 2 = 31

230 : 4 = 115 : 2 = 57,5

Tecnica n. 7: moltiplicare un numero per 5

Nota che 5 è la metà di 10.

Per moltiplicare un numero per 5 basta dividere il numero per 2 e moltiplicare il risultato per 10.

Esempi.

18 × 5 = 18 :2 × 10 = 90

86 × 5 = 43 × 10 = 430

54 × 5 = 27 × 10 = 270

Tecnica n. 8: dividere un numero per 5

Per dividere un numero per 5 basta moltiplicare il numero per 2 e dividere il risultato per 10.

Esempi.

125 : 5 = 125 × 2 : 10 = 250 : 10 = 25

80 : 5 = 160 : 10 = 16

64 : 5 = 128 : 10 = 12,8

Tecnica n. 9: moltiplicare un numero per 20, per 30, per 40, ...

Nota che:

20 = 2 × 10;

30 = 3 × 10;

40 = 4 × 10;

...

Per moltiplicare un numero per 20 basta moltiplicarlo per 2 e moltiplicare il risultato per 10.

Per moltiplicare un numero per 30 basta moltiplicarlo per 3 e moltiplicare il risultato per 10.

Per moltiplicare un numero per 40 basta moltiplicarlo per 4 e moltiplicare il risultato per 10.

...e così via, fino a 90...

Per moltiplicare un numero per 90 basta moltiplicarlo per 9 e moltiplicare il risultato per 10.

Esempi.

23 × 20 = 23 × 2 × 10 = 46 × 10 = 460

7 × 30 = 210

12 × 40 = 489

Tecnica n. 10: moltiplicare un numero per 9, per 19, per 29, ...

Nota che:

9 = 10 -1;

19 = 20 -1;

29 = 30 -1;

...

Per moltiplicare un numero per 9 basta moltiplicarlo per 10 e sottrarre dal risultato il numero stesso.

Esempi.

13 × 9 = 13 × 10 - 13 = 130 - 13 = 117

25 × 9 = 250 - 25 = 225

160 × 9 = 1600 - 160 = 1440

Per moltiplicare un numero per 19 basta moltiplicarlo per 20 e sottrarre dal risultato il numero stesso.

Esempi.

7 × 19 = 7 × 20 - 7 = 140 - 7 = 133

Per moltiplicare un numero per 29 basta moltiplicarlo per 30 e sottrarre dal risultato il numero stesso.

Esempio.

4 × 29 = 4 × 30 - 4 = 120 - 4 = 116

Tecnica n. 11: moltiplicare un numero per 11, per 21, per 31, ...

Nota che:

11 = 10 + 1

21 = 20 + 1

31 = 30 + 1

...

Per moltiplicare un numero per 11 basta moltiplicarlo per 10 e aggiungere al risultato il numero stesso.

Esempi.

24 × 11 = 24 × 10 + 24 = 240 + 24 = 264

15 × 11 = 150 + 15 = 165

310 × 11 = 3100 + 310 = 3410

Per moltiplicare un numero per 21 basta moltiplicarlo per 20 e aggiungere al risultato il numero stesso.

Esempi.

6 × 21 = 6 × 20 + 6 = 120 + 6 = 126

8 × 21 = 160 + 8 = 168

35 × 21 = 385

Tecnica n. 12: Usare la scomposizione in fattori 2, 5, 10, 100, ...

Per moltiplicare due numeri si possono scomporre in fattori opportuni e applicare le proprietà commutativa e associativa.

Questa tecnica è utile quando tra i fattori ci sono il 2, il 5, il 10, il 100, etc.

Esempio 1.

15 × 16 =

5 × 3 × 2 × 8 (scomposizione opportuna)

5 × 2 × 3 × 8 (proprietà commutativa)

10 × 24 (proprietà associativa)

240

Esempio 2.

240 × 25 =

2 × 2 × 6 × 10 × 5 × 5 =

2 × 5 × 2 × 5 × 10 × 6 =

10 × 10 × 10 × 6 =

6000

Altri esempi.

18 × 35 = 9 × 7 × 10 = 630

30 × 20 = 3 × 2 × 10 × 10 = 600

Tecnica n. 13: Usare il valore posizionale delle cifre

Per addizionare due numeri si possono addizionare separatamente le unità, le decine, le centinaia e poi fare il totale generale.

Esempio 1.

35 + 42 =

30 + 5 + 40 + 2 (uso del valore posizionale)

30 + 40 + 5 + 2 (proprietà commutativa)

70 + 7 = (proprietà associativa)

77

Per moltiplicare due numeri si può usare la proprietà distributiva di × rispetto a +.

Questa tecnica è utile quando uno dei due numeri è formato da una sola cifra.

Esempio 2.

7 × 23 =

7 × (20 + 3) = (uso del valore posizionale)

7 × 20 + 7 × 3 = (proprietà distributiva di × rispetto a +)

140 + 21 =

161

Tecnica n. 14: fare stime con la tecnica del "quasi"

Una stima è un calcolo veloce e approssimato. Il risultato da cercare non è proprio quello esatto ma è abbastanza vicino a quello esatto.

Esempio 1.

5,98 × 8,13 = ? (48,6174)

In casi come questo, si può fare il seguente ragionamento: 5,98 è quasi 6 e 8,13 è quasi 8.

Perciò:

5,98 × 8,13 = circa 6 × 8 = 48

In effetti, il risultato stimato è molto vicino a quello esatto, per difetto.

Esempio 2.

6,92 × 4,91 = circa 7 × 5 = 35 (il risultato esatto è 33,9772)

Questa tecnica funziona abbastanza bene quando i numeri si possono arrotondare senza troppo scarto.

In caso contrario, la stima è meno precisa.

Esempio 3.

7,65 × 3,42 =

circa 8 × 3 = 24 (il risultato esatto è 26,163)

Tecnica n. 15: fare stime usando poche cifre significative

Una variante della tecnica precedente è quella di arrotondare i numeri a 1 oppure 2 cifre significative e poi utilizzare le normali regole di calcolo

Esempi.

315 × 784 = circa 300 × 800 = 240.000 (il risultato esatto è 246.960, l'errore è del 3% circa)

126.478 × 12.147 = circa 130.000 × 12.000 = 1.560.000.000 (il valore esatto è 1.536.328.266, l'errore è del 1,5% circa)

Data creazione: marzo 2011

Ultimo aggiornamento: marzo 2011

×html 1.1

Sito Web realizzato da Gianfranco Bo