
[HOME - BASE Cinque - Appunti di Matematica ricreativa]
Attenzione: questo documento usa il tipo di carattere symbol.ttf per la visualizzazione di alcuni simboli matematici e delle lettere greche. Se non avete questo carattere installato nel vostro computer, alcune parti risulteranno illeggibili.
In tal caso vi consiglio di scaricare la versione in PDF, che risulta perfettamente leggibile.
Giuseppe Peano, Le definizioni in matematica (PDF)
Extret dels
ARXIVS DE L'INSTITUT DE CIENCIES
Any 1, Numero 1
Barcelona, 1911
I trattati di matematica procedono per definizioni e dimostrazioni.
I trattati di logica danno regole per le definizioni e dimostrazioni generali. Allora si presenta la questione di verificare se le definizioni e dimostrazioni matematiche soddisfino o no alle regole insegnate in logica scolastica e a quali regole speciali soddisfino.
OGNI DEFINIZIONE E' UNA EGUAGLIANZA
Ciò è chiaro nelle eguaglianze:
2 = 1+1
3 = 2+1
4 = 3+1
etc.
che si possono considerare come le definizioni delle cifre 2, 3, 4, etc. supposta nota la cifra 1, e il segno d'addizione +, anche limitato al caso in cui il secondo termine della somma è 1, cioè l'operazione + 1.
Sono pure eguaglianze le definizioni comuni dei numeri trascendenti

e della costante di Eulero:

Se il segno ideografico = non è scritto fra i due membri della definizione, esso è espresso con termini del linguaggio comune, cui si può sostituire.
Per esempio, la prima definizione di Euclide:
Shmeion estin, ou meroV ouqen
si può scrivere:
punto = "ciò che non ha parte"
La seconda definizione:
Grammh de mhkoV aplateV
ossia nella forma data da Legendre :
"La ligne est une longueur sans largeur"
può essere scritta:
linea = "lunghezza senza larghezza"
In questi esempi, e in numerosi altri, il segno = è posto non più fra due numeri, ma bensì fra due classi, cioè un nome comune punto, linea, e una frase composta di più parole.
In altri casi, il membro definito, che si suol scrivere il primo, è composto di più parole. Sono tali le comuni definizioni di "linea retta", di "numero primo", etc.
Il membro definito può anche essere una proposizione o una relazione.
Così la definizione del parallelismo fra due rette, in Euclide I 23, o ciò che fa lo stesso in Legendre:
"Deux lignes sont dites parallèles, lorsque étant situées dans le mème plan, elles ne se peuvent rencontrer à quelque distance qu'on les prolonge" può essere scritta:
"Due rette sono fra loro parallele" = "Esse giacciono in un medesimo piano, ed hanno nessun punto comune"
Parimente, la definizione di Euclide VII 13, può essere scritta:
"Due numeri sono primi fra loro" = "Essi hanno nessun divisore comune, oltre l'unità"
Quindi, per ridurre ogni definizione all'eguaglianza, è necessario usare il segno =, non solo fra due numeri, ma pure fra due classi, fra due proposizioni, e fra ogni specie di enti. Il segno di eguaglianza deve avere il valore generale espresso da Leibniz sotto la forma:
"Eadem sunt quorum unum in alterius locum substitui potest, salva veritate" che si può tradurre: "Due cose sono eguali, se ogni proprietà dell'una è pure proprietà dell'altra"
Con questi schiarimenti e generalizzazioni, la Regola precedente risulta dimostrata.
La proposizione della forma:
p = 3.1415...
non può essere una definizione, quantunque si presenti come un'eguaglianza; essa è un'eguaglianza impropria, indicando solo le prime cifre di p, o meglio essa significa in modo preciso:
3.1415 < p < 3,1416,
che non è un eguaglianza, e quindi non può essere una definizione.
Qualche rara proposizione data come definizione da qualche autore, non può ridursi ad eguaglianza, e quindi non può essere una definizione. Cosi la proposizione I 3,
di Euclide:
GrammhV de perata semeia
"gli estremi d'una linea sono punti", non può essere una definizione. Non è la definizione di punto, definito per la proposizione 1 sopra riportata; non è la definizione di linea, definita per la 2 ; non è la definizione di estremo, perché l'affermare che gli estremi della linea sono punti, esprime una proprietà degli estremi, che non basta a individuarli. La proposizione 3 ora citata ha il nome di definizione nella versione di Euclide fatta da Heiberg, in Lipsia 1883; ma il testo euclideo dà a tutte le proposizioni del capitolo il nome generico di oroi, e il greco oroV significa termino; la definizione è sempre indicata da Aristotele per orismoV Quindi la versione di Heiberg può essere impropria, e non dobbiamo rimproverare ad Euclide il piccolo difetto di aver chiamato definizione ciò che non lo è. La prima pagina di Euclide è pertanto una raccolta di termini o vocaboli, su cui si enunciano delle proprietà, che non sono necessariamente definizioni.
Secondo la nomenclatura generale, che noi adottiamo, ogni definizione ha la forma:
definito = definiente
ove il primo membro, o definito, indica il nome nuovo, o la proposizione nuova; e il secondo è una espressione composta con parole o segni, supposti prima noti. Però alcuni autori chiamano definizione, orismoV,, il nostro definiente,orizomenoV ;e fra questi si trova appunto Aristotele, che ora citeremo. Perciò questo avvertimento è necessario.
La regola finora studiata, si trova implicita in Aristotele. Citerò la versione di Barthèlemy Saint-Hilaire, Logique d' Aristote, Paris 1842.
Topiques livre VI § 1: "La définition (definiente) doit s'appliquer à tout le défini, et seulement au défini"
Idem livre VII § 7 : "les accidents qui sont à l'un devront aussi etre à l'autre". Questa condizione è simile alla definizione di eguaglianza data da Leibniz, e sopra riprodotta.
La stessa regola si trova in Leibniz, sotto la forma:
"Definitio est terminus aequivalens qui prodit per composito, substituendo simplices", ove la parola aequivalens indica appunto che deve essere una eguaglianza. Ed è più o meno chiaramente espressa da tutti i logici.
DEFINIZIONI REALI E NOMINALI
Aristotele classifica le definizioni in reali e nominali :
"O orizomenoV deiknusin h ti estin, h ti shmainei tounoma "
In matematica tutte le definizioni sono nominali, e perciò la classificazione non ha senso. Ciò è noto a tutti i matematici. Pascal, Pensées : " On ne reconnait en géométrie, que les seules définitions que les logiciens appellent définitions de nom"
Mobius, a.1815, Werke t. 1 pag. 388 : "Definitionum divisio in verbales et reales omni caret sensu"
E in generale per tutte le definizioni, in Stuart Mill, a. 1838: "AlI definitions are of names, and names only"
Ciò che in Storia naturale, alcuno chiama definizione reale, è detto da altri, e con maggior ragione, "descrizione. dell'animale o della pianta"
DEFINIZIONE PER GENERE E DIFFERENZA
Aristotele, Top. t. 8, pone la regola:
"O orismoV ek genouV kai diaforon estin"
che Boetio tradusse "per genus proximum et differentiam specificam"
L'esempio classico di questa proprietà è la definizione:
homo = animal rationale.
Qui "animal" e "rationale" indicano due classi, o, come dicono più spesso i matematici, ensemble, Menge, set, gruppo, etc. Fra quelle due classi è sottintesa l'operazione detta congiunzione dai grammatici, moltiplicazione logica dai logici dopo Boole, indicata in generale da et nel linguaggio comune, e in logica matematica dal segno Ç.
Quindi la regola di Aristotele direbbe che ogni definizione ha la forma:
x=a Çb
ove a e b sono classi note, dette genere e specie, e x è la classe che si definisce.
Qualche definizione matematica soddisfa alla regola Aristotelica. Così la definizione 22 di Euclide, che può tradursi:
quadrato = quadrilatero Ç equilatero Ç equiangolo.
Ma tale regola si può applicare al più alla definizione di una classe. Essa non è vera per la definizione del numero e, sopra citata, e per tutte le definizioni di numeri dell'analisi. Anche le definizioni di classi non hanno necessariamente la forma precedente. Per esempio:
numero composto = numero ´
ove per "numero" si intende intero maggiore di uno; cioè numero composto è il prodotto di un numero per un numero; fra le due classi, che in questo caso sono identiche, non è posto il segno di congiunzione logica Ç, ma il segno di moltiplicazione aritmetica.
Perciò la regola del "genus proximum et differentia specifica", che non si applica nella maggioranza dei casi, non può essere una regola.
DEFINIZIONI NEGATIVE
Aristotele critica e combatte le definizioni negative:
Top.VI § 5 : "On se trompe si l'on divise le genre par négation, comme ceux qui définissent la ligne une longueur sans largeur".
E a notarsi il fatto che Aristotele combatte la definizione adottata da Euclide un secolo posteriore. Ciò prova che i libri di Euclide sono la riproduzione di libri precedenti, cosa dimostrata del resto da molti argomenti.
Le definizioni negative sono numerose in matematica, e sono generalmente considerate esatte. Così :
"ligne courbe" = "ligne ni droite, ni composée de lignes droites" (Legendre)
"numero primo" = "numero non composto"
Esiste perfino in matematica una definizione con doppia negazione. Nella teoria dei numeri trasfiniti, di cui i principali risultati sono dovuti a G. Cantor, si dice che due classi hanno lo stesso numero, se gli elementi delle due classi si possono mettere in corrispondenza uno-uno. Una classe dicesi infinita se ha lo stesso numero di una sua parte; e dicesi finita se non è infinita; sicché la definizione ha la forma:
finito = non infinito
Se qui, al posto di "infinito" si scrive il suo equivalente "non finito" secondo etimologia, ne risulta un circolo apparente. In realtà non esiste, perché in questa teoria, "infinito" è considerato come idea semplice, e non nel suo valore etimologico. Frequente è in matematica l'uso di parole in senso speciale.
In conclusione, sonvi in matematica definizioni negative perfettamente rigorose.
ESISTENZA DELLA COSA DEFINITA
Alcuni logici affermano che si deve solo definire cose esistenti. Fra essi lo Stuart Mill, che partendo dalla definizione di cosa non esistente, e supponendola esistente, arriva a risultato assurdo. Ma l'assurdo deriva dal supporre esistente ciò che si è definito, non già dall'aver definito cosa non esistente.
Numerose sono le definizioni in matematica di cose non esistenti. Euclide libro IX prop. 20, dà un nome al massimo numero primo, e, ragionando su esso, conchiude che non esiste; cioè definisce un nome, allo scopo di provare che esso rappresenta nulla.
Le definizioni di limite, di derivata, di integrale di una funzione, non affermano l'esistenza dell'ente definito. La definizione di integrale è sempre seguita da una serie di proposizioni, della forma:
"Se la funzione è continua, esiste l'integrale"
"Se la funzione è crescente, esiste l'integrale"
"Condizione necessaria e sufficiente per l'esistenza dell'integrale è... "
Dalla definizione ordinaria:
"Derivata d'una funzione è il limite del suo rapporto incrementale"
risulta che la derivata esiste o non, secondo che esiste o non questo limite. Alcuni autori, per voler essere più rigorosi, dicono:
"Derivata è il limite, ove esista, del rapporto incrementale"
e allora se il limite non esiste, non si può più conchiudere che la derivata non esiste.
Del resto, la parola esiste ha più significati. La classe nulla rappresenta una classe in cui non esistono individui; ma essa esiste; cosi il numero 0 può indicare o l'assenza di grandezza, o la grandezza 0. In pratica conviene definire non solo cose esistenti, ma importanti.
DEFINIZIONE DELLE COSE CHIARE
Pascal dice "de ne point définir les choses claires et entendues de tous les homme et de définir toutes les autres". Questa regola non è assoluta.
Tutto il mondo ha, o crede di avere idea chiara di punto, linea, retta, piano, sfera. Ma è utile il sapere che la sfera si può definire:
"sfera di centro il punto o, e di raggio la quantità r" = "luogo dei punti che distano da o di r"
Invece le definizioni delle cose credute chiare: punto, linea, retta, etc. sono molto oscure; quelle nei comuni trattati sono molto discusse, ed occorre ben precisare ulteriormente la questione, per poter conchiudere se esse si possano definire, o non.
Il consiglio di Pascal può avere valore didattico. Si può dare un'idea di sfera colla visione del corpo fisico; in una scuola elementare si può fare a meno di darne la definizione logica, sopra riportata, e conviene certo di far a meno delle definizioni di linea e di retta, che sono oggi sempre più controverse.
DEFINIZIONI FINITE
M. Poincaré, nello studio di alcuni paradossi, di questi ultimi tempi, dice: "Je pense pour mon compte, et je ne suis pas le seul, que l'important c'estde ne jamais introduire des ètres que l'on ne puisse définir complètement en un nombre fini des mots"
Intesa letteralmente, questa regola è sempre applicata, poichè ogni definizione è sempre contenuta in poche linee di scritto, e le parole sono poche, e mai infinite. Sonvi però definizioni che involgono l'idea dell'infinito. Per esempio la definizione di derivata si applica ad infinite funzioni. Quasi tutte le definizioni matematiche involgono l'infinito.
DEFINIZIONI POSSIBILI
Ogni definizione è perciò una eguaglianza. Le altre regole esposte nei varii secoli, non hanno valore in matematica.
Affinché la definizione non si riduca ad un circolo vizioso, bisogna che nel secondo membro non ci sia il nome o segno definito nel primo. In alcune definizioni matematiche c'è nel secondo membro il segno definito del primo, ma in un altro senso. Cosi molti autori definiscono la somma di due frazioni mediante l'eguaglianza:

ove il segno di addizione + che si definisce nel primo membro, figura pure nel secondo. Ma nel primo, esso figura fra due frazioni, nel secondo fra interi; quindi la definizione non si può impugnare di circolo vizioso. Si può obbiettare da un altro punto di vista, di cui parleremo in seguito.
Diremo definizione possibile ogni eguaglianza, che contiene in un membro un segno, che non figura nell'altro, o vi figura con un valore differente.
Sono per esempio definizioni possibili del numero p le seguenti:

La prima è la definizione storica, ed è intelligibile al lettore che conosce gli elementi di geometria. La seconda, puramente analitica, indipendente da ogni idea geometrica, esige la conoscenza della teoria delle serie. La terza, pure analitica e semplice, esige il calcolo integrale. Ogni definizione possibile presenta i suoi vantaggi.
Immaginiamo disposte le idee che si considerano in un certo ordine. Per esempio, durante la nostra vita noi acquistiamo le idee in un ordine. Si dirà definizione possibile relativamente ad un dato ordine, una eguaglianza che contiene nel primo membro un segno, e nel secondo una espressione composta con segni precedenti esso. Per esempio, le tre definizioni possibili date di p, sono rispettivamente possibili a chi conosce la geometria elementare o la teoria delle serie, o il calcolo integrale.
Fra le varie definizioni possibili di un ente, in un ordine fissato, la scelta della definizione reale dipende dalla volontà dell'autore consigliato da ragioni didattiche. Quindi una proposizione può essere o non una definizione possibile; ciò dipende dalla sua natura. L'essere una proposizione una definizione, dipende dalla volontà dell'autore, e non solo dalla natura della proposizione.
Aprendo un trattato di matematica verso la sua metà, ogni nuova parola è definita per mezzo di quelle studiate nelle pagine precedenti. Ciò non avviene per le prime definizioni, e gli autori non sogliono dire quali idee essi suppongono premesse. Ma, se essi non lo dicono, è però possibile il fame il catalogo. Considero per esempio le prime definizioni di Euclide-Legendre:
"La ligne est une longueur sans largeur"
"La surface est ce qui a longueur et largeur, sans hauteur ou épaisseur"
Vediamo in esse definite le parole "linea, superficie" per le idee geometriche non prima definite "lunghezza, larghezza, altezza, spessore". Le idee che figurano nei secondi membri sono più numerose che quelle nei primi. E allora è naturale il domandarsi, se non convenga sopprimere queste definizioni, assumendo come idee non definite linea e superficie. Ed invero l'idea di lunghezza, che qui si da come intuitiva, è poi definita nei trattati di calcolo, e la definizione non è semplice.
Alcuni autori presuppongono nota la lingua volgare. Ma appartengono alla lingua volgare i termini "punto, linea, piano, sfera, uno, due, tre", etc. Perciò l'analisi della questione, se gli elementi più semplici della geometria, e le idee di numero, e le più semplici di aritmetica, si possano definire o non, esige l'analisi della lingua volgare, alla enumerazione di tutte le parole e flessioni grammaticali, che si presentano nelle prime pagine di queste scienze, e quindi alla ricostruzione della ideografia.
IDEE PRIMITIVE
Dato un ordine alle idee d'una scienza, non tutte si possono definire. Non si può definire la prima idea, che non ha precedenti; non si può definire il segno =, che figura in ogni definizione. Si dice che una idea è primitiva, relativamente ad un dato ordine, se, in quest'ordine delle idee, essa non si sa definire. Perciò l'essere una idea primitiva, non è un carattere assoluto, ma solo relativo. La questione "l'idea di punto è essa primitiva, o si può definire? ", non ha senso preciso, se noi non prefissiamo quali idee si suppongono note.
L'esistenza di idee primitive già è chiaramente espressa in Pascal:
"Il est évident que les premiers termes qu'on voudroit définir en supposeroint des précédents pour servir à leur explication... et ainsi est clair qu'on n'arriveroit jamais aux premièrs. Ainsi en poussant les recherches , de plus en plus, on arrive nécessairement à des mots primitifs, qu'on ne peut plus définir"
I comuni trattati di Aritmetica e di Geometria contengono un grande numero di idee primitive, cioè che essi non definiscono, quantunque non ne diano il catalogo.
La determinazione delle idee primitive della matematica diede luogo, in questi ultimi venti anni, a numerosissimi studii, quasi tutti fatti col sussidio della ideografia della logica-matematica.
Citerò in modo speciale i lavori di Burali-Forti, Padoa, Pieri in Italia, Korselt in Germania, Gérard in Francia, Russell e Whitehead in Inghilterra, Bòcher, Dickson, Huntington, Veblen in America.
Fra questi giunse a meritata fama il Pieri, ora prof. all'università di Parma, che nel 1898-99 pervenne al esprimere tutte le idee di Geometria, prima mediante tre, poi mediante due sole idee primitive: "punto, e distanza fra due punti" (1). Nello stesso periodo di tempo il prof. Hilbert di Gottingen, che pure fece profondi studii sui fondamenti, senza però servirsi della logica-matematica, era arrivato a decomporre le idee di Geometria in otto, date come primitive : "punto, retta, piano, situato, entro, parallelo, congruente, continuo" (2).
Quindi ben meritato è l'elogio che dei lavori del prof. Pieri fa B. Russell, nel suo grande e celebre libro: The principles of mathematics : "This is, my opinion, the best work on the present subject ".
(1) I principii della Geometria di posizione, Memorie Academia Torino,1898. Della Geometria elementare come sistema ipotetico deduttivo, Idem, 1899.
(2) Grundlagen der Geometrie, Leipzig, 1899.
Le proprietà fondamentali delle idee primitive sono determinate da "proposizioni primitive", o proposizioni che non si dimostrano, e da cui si deducono tutte le altre proprietà degli enti considerati. Le proposizioni primitive, che sono all'incirca gli assiomi o postulati degli antichi geometri, in generale sono evidenti, quantunque questo carattere sia relativo alla persona, e non a rigore necessario. Le proposizioni primitive fungono in certo modo come definizioni delle idee primitive. Gli autori citati esposero per le varie parti della matematica, più sistemi completi di idee primitive, e di proposizioni primitive.
LOGICA-MATEMATICA
Immaginiamo il vocabolario di tutte le parole che si presentano nei libri di matematica. Alcune di queste appartengono evidentemente alla geometria, come "punto, retta". Altre all'Aritmetica, come "numero, addizione". Altre alle matematiche superiori, come "derivata, integrale". Oltre a queste si hanno numerose parole, le stesse sia che si consideri un trattato di algebra o di geometria. Lo studio di quelle parole, compresi i suffissi grammaticali, che unite a termini proprii della matematica, permettono di esprimere tutte le proposizioni matematiche, appartiene a quella nuova scienza, che si chiama Logica-matematica.
La Logica-matematica contiene in sé una parte, di studio grammaticale; ma non di tutta la grammatica. In matematica per esempio, i verbi sono sempre alla terza persona, e al così detto tempo presente, perché la verità delle proposizioni matematiche è indipendente dall'io, e dal tempo.
La logica-matematica studia le idee rappresentate dalle parole sopra indicate, le loro proprietà, e le regole delle definizioni e dimostrazioni che si incontrano in matematica.
Leibniz fu il primo a isolare alcune idee di logica-matematica, enunciandone le proprietà. Gli studii di Leibniz rimasero sepolti per lungo tempo. Boole nel 1847 ritrovò per via indipendente parecchie idee di questa scienza.
Schroeder, nel 1877 fece una teoria semplice ed elegante delle classi che qui esporrò per sommi capi, coi simboli attuali.
CALCOLO DELLE CLASSI
"Classe" è la prima idea che consideriamo. Essendo essa la prima idea, non si definisce. La definizione scritta. in qualche libro:
"classe è l'insieme degli enti che soddisfano ad una medesima proprietà"
è un circolo vizioso manifesto. Invero classe e insieme sono sinonimi, come il francese ensemble, l'inglese set, il tedesco Menge, usati specialmente dai matematici, sono sinonimi della parola internazionale classe. Classe e proprietà sono poi sinonimi, non linguisticamente, ma per valore; poichè sussiste l'equivalenza:
"appartenere ad una classe" = "avere una proprietà"
sicchè classe e proprietà differiscono solo per la funzione grammaticale, che l'uno è accompagnato del verbo appartenere, e l'altro da avere; così astro e stella differiscono fra loro, in ciò, che l'uno è accompagnato dall'aggettivo al mascolino, e l'altro al feminino.
Indicheremo con a, b, c, ...delle classi qualunque, seguendo l'uso da Aristotele ai matematici moderni.
Considereremo il segno di relazione =, ben noto in algebra; e un segno di operazione Ç; sicché a Ç b indica la classe comune ad a e a b, o l'insieme degli individui che sono a e b. Leggeremo il segno Ç , colla congiunzione latina et.
Rappresentando le classi con figure nel piano, per esempio coi cerchi usati da Eulero, e prima ancora da Leibniz, si ha una idea sensibile delle varie classi e operazioni che introdurremo.
Sussistono le identità:
a Ç b = b Ç a
a Ç(bÇ c) = (a Ç b) Ç c
a Ç a = a
La prima esprime la proprietà che in algebra si chiama commutativa; la seconda la proprietà associativa. L'addizione e la moltiplicazione aritmetica hanno queste proprietà. La terza fu già espressa in simboli e in parole da Leibniz : "Repetitio ejusdem literae in eodem termino est inutilis". Essa fu chiamata legge di semplicità da Jevons, perchè rende il calcolo delle classi più semplice del calcolo algebrico sui numeri.
Se per a Ç b, ove a e b sono numeri, si intende il massimo dei numeri a e b, sussistono le tre leggi sopra scritte. Lo stesso se invece di massimo, si legge minimo, o massimo comun divisore, o minimo comune multiplo dei numeri dati.
L'operazione Ç dicesi moltiplicazione logica, perché ha le due prime proprietà della moltiplicazione, ma specialmente perché la maggioranza degli autori sopprime il segno di operazione, scrivendo ab invece di a Ç b.
Siccome l'addizione e la moltiplicazione aritmetica hanno la proprietà commutativa e l'associativa, ne risulta che questa proprietà non è conseguenza di quelle. Possiamo riconoscere che la proprietà commutativa e l'associativa non sono conseguenza delle altre due, col portare esempi di operazioni che hanno due delle proprietà, e non la terza.
Prenderò gli esempi dalla interessantissima memoria: Huntington, Sets of independent postulates for the algebra of logic. Transactions of the American mathematical society, 1904.
Se per a Ç b intendo il primo dei due elementi, cioè a, sussistono evidentemente le proprietà associativa, e di semplicità, ma non la commutativa.
Per fare altri esempi, osserviamo che se gli elementi a, b,... che si possono considerare, appartengono ad un sistema di un numero finito di elementi, si può definire una operazione su due elementi, che si potrà chiamare loro prodotto, col dare ad arbitrio una tavola a doppia entrata, che si potrà chiamare tavola di moltiplicazione. Se gli elementi sono due, chiamandoli 0 e 1, le tavole che danno il prodotto di due elementi, ove il primo si legga a sinistra, indicante la linea, e il secondo fattore in alto, indicante la colonna, quando per ab si intenda il massimo, o il minimo, o il primo, sono rispettivamente:
| 0 | 1 | |
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
Se l'operazione ha la proprietà semplificativa, cioè aa = a, risultano determinati gli elementi della diagonale principale, da alto-sinistra in basso-destra.
Se l'operazione è commutativa, la tavola di moltiplicazione è simmetrica rispetto alla diagonale principale. Perciò una operazione in un campo a due elementi, commutativa e semplificativa, è necessariamente o il massimo o il minimo, e quindi è associativa.
Una operazione fra tre elementi 0, 1, 2, commutativa e semplificativa, e non associativa; è indicata dalla tabella seguente:
| 0 | 1 | 2 | |
| 0 | 0 | 2 | 1 |
| 1 | 2 | 1 | 0 |
| 2 | 1 | 0 | 2 |
in cui a due elementi non eguali si fa corrispondere il terzo. Ivi (01)2 = 22 = 2, mentre (0)12 = 00 = 0
Così risulta dimostrato che le tre proprietà della congiunzione logica sono fra loro indipendenti, ed abbiamo dato un esempio del come si provi l'indipendenza di un sistema di proposizioni. Questo metodo di prova ebbe larga applicazione in questi ultimi anni, in aritmetica e in geometria, per opera dei professori Padoa, Burali, Russell, Veblen, Pieri, e di tutti i cultori della logica-matematica.
Alcuni autori proposero, dato un sistema di proposizioni, di provarne la compatibilità: e fra questi Hilbert. Ma questa prova è inutile se noi prendiamo le proposizioni da un soggetto reale. Per esempio le proposizioni precedenti sussistono, se ab indica la classe comune alle classi a e b, quale è lo scopo del nostro studio. Quindi è curioso, ma non necessario, l'aggiungere, che esse valgono pure in altre interpretazioni, come "minimo multiplo comune". La prova della coesistenza sarebbe necessaria, se si prendono le proposizioni a caso, e non si studia un qualche soggetto reale.
Avendo a Ç b il significato logico sopra spiegato, l'eguaglianza
a = ab
esprime la proposizione universale affermativa "ogni a è b". Essendo questa relazione molto importante, si suole indicarla con un segno: a É b (1).
(1) Il segno É, che si può leggere "è contenuto" è l’iniziale capovolta della relazione inversa "contiene".
Quindi si pone:
Definizione. a É b significa a = ab.
Ne risulta:
Teorema. a É a.
Infatti, per la 3, a = aa, che è appunto la proposizione a dimostrarsi.
Teorema. ab É a.
Infatti, ab = a(ab), per le proprietà 2 e 3.
Teorema. Se a É b, e b É a, resulta a = b.
Infatti, per definizione, a = ab, b = ba, e per la 1, a = b.
Teorema. Se a É b, e b É c, si ha a É c.
Infatti, dalle ipotesi si ha a = ab, e b = bc, onde a = a(bc) = (ab)c = ac, cioè a É c.
Questa ultima proposizione è il sillogismo, sotto la prima figura, o in Barbara. In modo analogo, si dimostrano facilmente le proposizioni.
Se a É b, e a É c, si ha a É bc.
Se a É b, sarà ac É bc.
Se a É b, e c É d, sarà ac É bd.
Però non bisogna illudersi sul significato di queste dimostrazioni. Per dimostrare la proposizione, che dicemmo sillogismo, si fecero dei sillogismi, e si applicarono più forme di ragionamento, comuni in matematica, ma che noi non abbiamo ancora analizzato.
Quindi in realtà, nei ragionamenti precedenti, noi non abbiamo dimostrato alcuna regola di logica; ma semplicemente, ammesse le forme di ragionamento, comuni in matematica, e ammesso che una certa operazione, indicata col simbolo Ç, abbia le proprietà 1, 2, 3, ne risulta che essa ha tutte le proprietà successive.
SEGUE IL CALCOLO DI CLASSI
In logica-matematica si considerano altre operazioni e enti, di cui darò un rapido cenno.
Il simbolo Æ rappresenta la classe nulla o vuota, che può benissimo risultare dal prodotto di due classi effettive. Qualunque sia la classe a, si ha :
a Ç Æ = Æ, o in altri termini, Æ É a
a È b indica la classe degli individui che sono o a o b. Questa operazione ha le proprietà:
a È b = b È a,a È (b È c) = (a È b) È c,a È a = a,
identiche a quelle del segno di congiunzione Ç Fra i due segni che leggeremo et e aut, passano poi le relazioni
a Ç (b È c) = (a Ç b) È (a Ç c), a È (b Ç c) = (a È c) Ç (b È c), a È Æ = a.
In molti scritti di logica simbolica, si introduce un simbolo, V, per indicare la classe totale; ma questo simbolo si è mostrato di nessuna utilità nelle applicazioni della logica alla matematica; inoltre l'idea del tutto assoluto è una idea non chiara; si hanno solo dei tutto relativi. E precisamente dalla sua considerazione dipendono alcuni paradossi su cui tanto si discusse in questi ultimi anni.
Data la classe a, con -a, leggasi "non a", si intende la classe degli individui che non sono a.
Si hanno le formule:
-(a Ç b) = -a È -b, -(a È b) = -a Ç -b
cioè la negazione di et è aut, e la negazione di aut è et.
Ma anche il segno di negazione generale è un po' indeterminato, non dicendoci dove si debbano prendere i non-a.
Ha invece senso chiaro l'espressione
b-a, i b che non sono a.
Per più ampi studii di queste operazioni logiche, e raccolta di formule, vedasi il Formulario mathematico, da me edito, specialmente il volume 3.
Coi simboli dell'aritmetica e dell'algebra si possono esprimere completamente alcune proposizioni, come:
2+3 =5
5>2
etc.
In generale però le proposizioni di analisi sono espresse parte in simboli e parte con parole. Introducendo i simboli logici, si può scrivere un maggior numero di proposizioni simboliche. Scriviamo N invece di numero; essendo a un numero, N ´ a significhi prodotto di un numero per a, o multiplo di a. Si ha:
4 ´ N É 2 ´ N,
cioè ogni multiplo di 4 è un multiplo di 2.
(2 ´ N) Ç (3 ´ N) = 6 ´ N,
"I multipli di 2, e contemporaneamente multipli di 3 sono multipli di 6".
(4 ´ N) È (6 ´ N) É 2 ´ N,
"I numeri che o sono multipli di 4 o multipli di 6 sono multipli di 2".
Questa ultima proposizione si può anche leggere: "i multipli di 4 e i multipli di 6 sono multipli di 2", sicché il segno È,che leggiamo aut, viene qui a corrispondere all'et del linguaggio comune. Non esiste una corrispondenza univoca tra le parole e i simboli; i simboli sono determinati mediante le loro proprietà, e non sono abbreviazioni stenografiche delle parole con cui proponiamo di leggerli. Così il segno di aritmetica +, si legge più, e si crede una deformazione fatta nel 1500 della lettera p, iniziale di plus. Ma esso è ora un simbolo, non una abbreviazione semplice.
Così la frase "somma di a con b", si scrive in simboli, "a + b", col segno + che non sta nel linguaggio comune.
Invece la frase, "a è più grande di b" si scrive, a > b senza segno + , benché nel linguaggio comune ci sia la parola più.
CALCOLO SU PROPOSIZIONI
Indipendentemente dalla teoria delle classi, alcuni autori, fra cui il Peirce nel 1880, costrussero un calcolo sulle proposizioni. Gli autori che indipendentemente trovano le stesse cose, introducono simboli differenti. Cosi nella teoria geometrica dei vettori, noi abbiamo una moltitudine di notazioni differenti, essendo essa stata scoperta più volte durante l'ultimo secolo. Colle notazioni precedenti, se a, b, c, sono proposizioni,
a Ç b indica la loro affermazione simultanea,
a É b indica che da a si deduce b..
Æ indica la proposizione assurda.
a È b indica una delle due proposizioni a e b è vera
-a indica la negazione di a.
Tutte le identità su classi sussistono fra proposizioni. Si hanno poi proprietà speciali. Ma per ben stabilire questa proprietà, bisogna distinguere le proposizioni senza lettere variabili, o categoriche, come 2 + 3 = 5, su cui nessun calcolo logico è adottato in matematica, dalle proposizioni che contengono una variabile, e che esprimono una condizione, e dalle proposizioni che ne contengono due e sono delle relazioni, etc.
Essendo a una classe, con "xÎa" indicheremo la proposizione singolare "x è un a" o "x è un individuo della classe a". Il segno Î è l'iniziale di esti.
Bisogna ben distinguere la proposizione singolare "x Î a" cioè "x è un individuo della classe a", dalla universale "x É a", cioè "ogni x è a " quantunque il linguaggio comune spesso li confonda.
La prima relazione esprime una proprietà di x;la seconda una proprietà degli individui di x. Ma più che le discussioni col linguaggio comune, si vede la differenza delle idee dalle loro differenti proprietà.
La relazione É è transitiva, cioè da a É b, e da b É c, resulta a É c, che è il sillogismo.
La relazione Î non lo è. Infatti da "a è un punto della retta punteggiata b, e b è una retta del fascio c " ovvero "7 è un numero primo, e numero primo indica una classe infinita" non si può conchiudere col sillogismo.
La forma scolastica del sofisma è "Pietro e Paolo erano apostoli, ma gli apostoli erano dodici; dunque Pietro e Paolo erano dodici". Gli scolastici già distinguevano il "sensus compositi" del Î, dal "sensus divisi" del É.
La relazione Î è distributiva rispetto ad È ; cioè la x Î N ´ 2 È N ´ 3, significa x è multiplo di 2, o x è multiplo di 3.
Invece la relazione É non lo è. Così da (N + 1)2 É 4N È (4 N + 1), ogni quadrato di un numero maggiore di 1 o è un multiplo di 4, o un multiplo di 4 più 1, non segue che ogni quadrato sia un multiplo di 4, o che ogni quadrato sia un multiplo di 4 più 1.
Schroeder, cui dobbiamo la voluminosa opera "Algebra der Logik", non pervenne a distinguere le due operazioni Î e É; quindi non poté costrurre un calcolo logico; essendo impossibile costrurre un calcolo con un simbolo che è e non è transitivo, che è e non è distributivo rispetto ad È; etc.
La proposizione x Î a indica una condizione in x.
Viceversa, data una condizione contenente una lettera variabile x, e sia p, con (x ' p) indichiamo la classe degli x che soddisfano alla condizione, p, sicchè posto a = (x ' p), ne resulta p = (x Î a), ossia ogni condizione p si può ridurre alla forma x Î a, ove a è una classe.
In una formula, una variabile x si dice reale, se il valore della formula dipende dalla variabile. La variabile dicesi apparente, se il valore della formula ne è independente. Questa distinzione è della massima importanza. Nelle formule analitiche
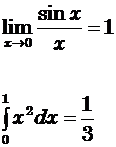
la lettera x è apparente nei primi membri, ed è scomparsa nei secondi.
Se p è una condizione in x, la scrittura x ' p contiene la lettera x apparente; poiché ad es,
x ' (x2 - 3x + 2 = 0),
cioè la classe delle radici della equazione in x:
x2 - 3x + 2 = 0
è identica ad
y ' (y2 - 3y + 2 = 0).
Allora se p e q sono condizioni nella lettera x, la proposizione
x ' p É x ' q
indica una proposizione in cui la lettera x è apparente.
Si può scrivere p Éx q, "da p si deduce, per rapporto ad x, la q", e si può sottintendere l'indice x al segno di deduzione scrivendo p É q, e leggendo "da p si deduce q", ove non siavi pericolo di ambiguità nella lettera rispetto cui si fa la deduzione, e precisamente, se l'ipotesi e la tesi contengono la sola lettera reale x.
Se la proposizione che si considera contiene due o più variabili reali, cioè è una relazione, si considera l' insieme di due variabili come un nuovo ente, indicato con x;y, che si legge la coppia formata da x e y. Se x e y sono dei numeri reali, rappresentati da punti su di una retta, x; y sarà rappresentato dal punto del piano, di coordinate x e y. La terna x; y ;z si definisce come (x; y); z, cioè come la coppia formata dalla coppia x; y e da z.
OGNI DEFINIZIONE DEVE ESSERE SIMBOLICA
Se le definizioni di matematica superiore, espresse col linguaggio ordinario, o anche parzialmente in simboli, possono parere soddisfacenti, non siamo mai certi che la definizione non contenga un circolo vizioso, nascosto in qualche parola o ipotesi, se non si è ridotta completamente in simboli. Per esempio, molti autori definiscono la serie come segue:
"Dicesi serie la successione di quantità formate con legge determinata"
ove la serie è definita mediante successione e legge, che dovrebbero alla loro volta essere definite.
Come pure la definizione di funzione:
"Si dice che y è funzione di x, se ad ogni valore di x corrisponde un valore di y" è un circolo vizioso evidente, definendosi la parola ignota funzione mediante la ignota corrispondenza. Alcuni dicono:
"Si dice che y è funzione di x, se per ogni x, si ha un valore di y" e allora il circolo vizioso è più nascosto, essendo la corrispondenza rappresentata dalla preposizione per, di cui si può domandare la definizione.
Scriveremo, per abbreviare a, b Î u, invece di (a Î u) (b Î u), e leggeremo secondo il linguaggio comune a e b sono u.
Divideremo le varie parti di una proposizione con dei punti, onde fare economia di parentesi. Allora la proposizione:
a,b Î Cls .É. (a É b)=(x Î a .É. x Î b)
"se a e b sono classi, allora la proposizione universale: ogni a è b, equivale, alla deduzione: da x è un a, segue qualunque sia x, che x è un b", contiene in un membro il É fra classi e nell'altro fra proposizioni.
Sarebbe però una illusione il credere che essa possa servire come definizione del É fra proposizioni mediante quello fra classi; perché l'eguaglianza-definizione contiene l'ipotesi e poi il segno di deduzione fra proposizioni. Invece, supposto noto il valore del segno É fra proposizioni, essa è una definizione possibile dello stessi segno fra classi.
La proposizione
a, b Î Cls É (x Î a Ç b) = (x Î a) Ç (x Î b)
contiene nel secondo membro il segno di moltiplicazione logica Ç fra proposizioni e nel primo fra classi.
Ma non si può definire il secondo mediante il primo, perché l'ipotesi a, b Î Cls è appunto già l'affermazione del prodotto logico "a Î Cls" e "b Î Cls", cioè l'idea che si cerca di definire, si trova già nella ipotesi.
Ma si può definire il prodotto logico di classi, mediante quello fra proposizioni, leggendo la formula precedente:
a, b Î Cls .É. a Ç b = x ' (x Î a, x Î b)
"indicando con a e b due classi, con a Ç b si intende l'insieme degli x che soddisfanno alle due condizioni x Î a e x Î b".
Questa definizione contiene. una ipotesi. Le definizioni con ipotesi sono numerose in matematica. Quando si definisce una espressione contenente variabili in generale si comincia con dire che cosa indicano queste variabili.
OMOGENEITA' DELLE DEFINIZIONI
Ogni definizione deve contenere nei due membri che la costituiscono, le stesse variabili reali. Esprimiamo questa regola dicendo che essa deve essere omogenea; e passiamo a studiare questa nuova regola.
Se ciò che si definisce è un simbolo costante, il membro definiente, se contiene variabili, le deve contenere solo apparentemente. Cosi la definizione già citata di e :

per m infinito, è omogenea, perché il primo membro contiene il simbolo costante e, ed il secondo contiene la sola variabile m, la quale è apparente, perché accompagnata dalla operazione limite.
La ragione della omogeneità risulta evidente. Se indico con un nome costante una espressione che può assumere più valori, avrò dato lo stesso nome a più cose differenti fra cui poi risulta impossibile il distinguere.
In matematica spesso la forma delle definizioni è difettosa. La definizione della risultante di due forze, come quella che ha per componenti rispetto ad assi coordinati le somme delle componenti delle forze date, che si trova in Kirckhoff, definisce la risultante delle due forze non solo mediante queste forze, ma ancora mediante gli assi di riferimento. Altre definizioni geometriche in cui si fa uso di assi coordinati, non sono omogenee.
La formula:

esprime la comune regola per la somma delle frazioni.
Ma, contrariamente a ciò che fanno più autori, non si può assumere come definizione, essendo contro al principio di omogeneità. Invero, dati i numeri a e b, resulta determinato il valore della frazione a/b; ma viceversa, data una frazione x, questa si può mettere sotto infinite forme a/b; ossia, mentre il valore della frazione è funzione del numeratore e del denominatore, invece il numeratore e denominatore della frazione non sono funzioni della frazione; poichè 1/2 = 2/4, e il numeratore della prima non eguaglia il numeratore della seconda.
Nel caso della formula precedente, il primo membro è una funzione delle due variabili a/b e c/d; mentre il secondo è funzione delle quattro variabili a, b, c, d. Quindi la proposizione, considerata come definizione, non è omogenea. La stessa obbiezione si può mettere sotto altra forma. La definizione della somma di due frazioni deve avere la forma:
x, y Î frazioni .É. x + y = espressione composta con x, y, e con segni noti.
Tale non è l'eguaglianza sopra considerata, perché nel secondo membro figurano i numeratori e i denominatori di x e y, che non sono determinati univocamente dati x e y.
Il numero irrazionale è il limite di razionali. Il limite può essere variamente considerato, come limite superiore o inferiore d'una classe, come limite di separazione di due classi contigue, come limite verso cui converge una successione. In ogni caso, il numero irrazionale è funzione della classe o della successione, ma la classe o successione non è funzione del numero irrazionale, potendo lo stesso irrazionale essere definito da più classi. Quindi gli autori, e sono ancora numerosi, che definiscono la somma di due irrazionali ricorrendo ad una loro rappresentazione, peccano contro l'omogeneità.
Per vedere meglio che non è permesso di definire una operazione sulle frazioni mediante una loro rappresentazione, permettiamoci di definire, x m y, medio di due frazioni x e y, la frazione che ha per numeratore la somma dei numeratori e per denominatore la somma dei denominatori. Cioè poniamo.

formula dello stesso tipo della precedente.
Si avrà (1/2) m (2/3) = 3/5, (2/4) m (2/3) = 4/7,
e poiché 1/2 = 2/4,
resulterebbe 3/5 = 4/7, resultato falso.
In matematica sonvi molte espressioni che hanno la forma grammaticale di funzioni e non lo sono. Oltre a numeratore e denominatore di una frazione, le parole: termini d'una somma, fattori di un prodotto, coefficiente, base, esponente, non sono funzioni del valore della espressione, ma della sua forma. Parimenti le parole: monomio, binomio, frazione irreduttibile, esprimono proprietà della forma, non del valore della espressione. Nella ideografia, queste parole non possono essere rappresentate da simboli. Quindi si vede che il numero dei simboli del Formulario mathematico sia molto minore delle parole del linguaggio comune, non potendo essere trasformate in simboli le pseudofunzioni e le pseudoclassi, e non essendo opportuno di introdurre un simbolo nuovo per sostituire una combinazione semplice di simboli noti.
UTILITA' DELLE DEFINIZIONI
Se una definizione è ben data, al posto del simbolo definito si potrà sempre sostituire il membro definiente, e perciò eliminare da tutta la teoria il simbolo definito. Questa eliminazione è cosa molto importante. Se eliminando il simbolo definito, la nuova esposizione non è più lunga e più complicata della precedente, ciò significa che quella definizione era poco utile. Se si incontrano difficoltà nella eliminazione, ciò prova che la definizione non fu ben data; anzi questo metodo della sostituzione è il migliore per riconoscere l'esattezza d'una definizione.
Resulta che in teoria, nessuna definizione è necessaria; però in pratica esse sono tanto utili da essere quasi necessarie.
Le definizioni, in teoria sono arbitrarie. Dice Pascal: "les définitions sont très libres, il et elles ne sont jarnais sujettes à ètre contredites, car il n'y a rien de plus permis que de ne donner à une chose qu'on a clairement désignée, un nom tel qu'on voudra". Leibniz pone però una limitazione pratica: "Definitiones per se quidem sunt arbitrariae, usui di tarnen accomodari et communi sociorum consensu probari debent". Non sempre le definizioni matematiche soddisfano a questo consiglio pratico di Leibniz; per esempio alcuni autori definiscono il massimo di una funzione in modo da attribuirci un valore un po' diverso dall'uso comune, traendo in errore il lettore poco attento.
Un altra legge pratica che regge le definizioni e le notazioni matematiche, è il così detto principio di permanenza, o principio di conservazione delle leggi formali. Questo principio impone che quando si stabilisce un nuovo sistema di notazioni, o un nuovo calcolo conviene fare in modo che il nuovo calcolo sia simile per quanto è possibile ai calcoli antichi, sicché lo studioso non debba imparare tutto un nuovo calcolo, ma solo le differenze colla teoria a lui nota. Questo principio corrisponde al principio dell'economia del pensiero, e del minimo lavoro.
Le idee precedenti sono accennate e sparse nei volumi del Formulario mathematico. Il materiale storico e le citazioni di Aristotele e di Pascal mi furono fornite dalla Dott. Maria Gramegna, ora prof. in Avezzano, e prima studente all'Università di Torino. E ringrazio l'egregio amico Prof. D'Ors del suo cortese invito a collaborare in questo archivio.
Università, Torino.
------------------------
Se trovate errori e/o omissioni, vi prego di segnalarle a:
Gianfranco Bo
gfbo@quipo.it
------------------------
Data creazione: ottobre 2007
Ultimo aggiornamento: ottobre 2007
html 4.01
Sito Web realizzato da Gianfranco Bo