
[HOME - BASE Cinque - Appunti di Matematica ricreativa]
C'Ŕ stato un periodo in cui i Geometri avevano la passione per le torri
Un particolare ringraziamento a: http://www.malhatlantica.pt/mathis/Histˇria da Matemßtica - histˇria dos problemas e a Panurgo per gli importanti contributi alla risoluzione dei problemi.
La scala fra due torri
Due torri sono alte rispettivamente 20 m e 24 m, e distano 22 m l'una
dall'altra.

In quale punto del suolo deve essere posata una scala in modo che,
appoggiata all'una o all'altra torre, ne raggiunga esattamente la cima?
Quanto deve essere alta la scala?
La torre, il fossato e la scala (Peter van Halle, 1568) |
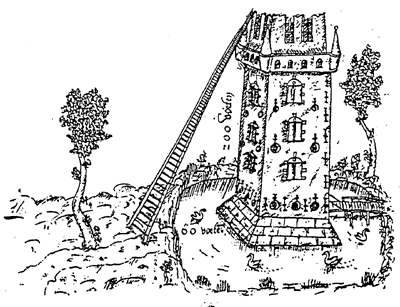 |
| Scala e torre della stessa altezza Una scala alta 20 braccia Ŕ appoggiata ad una torre alta 20 braccia. La base della scala si trova a 12 braccia di distanza dalla base della torre. Quanto Ŕ pi¨ bassa la cima della scala rispetto alla cima della torre? (Gaspar Nicolas, Prßtica D'aritmÚtica, 1519) |
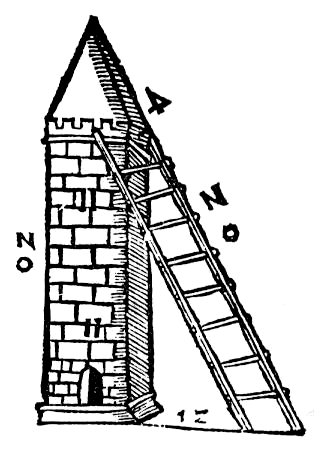 |
L'albero spezzato
C'Ŕ un albero alto 50 braccia sulla riva di un fiume largo 30 braccia.
Il caso vuole che l'albero si spezzi in un punto tale che la sua cima tocchi
la riva opposta del fiume.
Voglio sapere quante braccia di albero si sono rotte e quanto ne rimane
ritto.
La canna appoggiata ad una parete
Una canna Ŕ appoggiata obliquamente ad un muro verticale. La cima della
canna tocca la sommitÓ del muro.
Se la cima della canna si abbassa di 3 GAR allora la sua base si allontana
dal muro di 9 GAR.
Quanto Ŕ lunga la canna?
Quanto Ŕ alto il muro?
(tavoletta babilonese del III sec. a. C.)
| La torre, il fiume e la fune Una torre alta 40 braccia si erge in riva ad un fiume largo 30 braccia. Voglio sapere quanto sarÓ lunga una fune che colleghi la cima della torre con la riva opposta del fiume.
Filippo Calandri, 1491 |
|
| Le due torri e la fonte Due torri alte rispettivamente 90 braccia e 80 braccia distano 100 braccia fra loro. Fra le due torri si trova una fonte in un luogo tale che se due uccelli uguali partissero contemporaneamente dalle cime delle due torri arriverebbero a bere alla fonte nello stesso istante. Chiedo, quanto dista la fonte da ciascuna torre? (si suppone che gli uccelli volino alla stessa velocitÓ) (Gaspar Nicolas, Prßtica D'aritmÚtica, 1519) |
|
| Le torri e i passeri Due passeri iniziano a volare contemporaneamente e alla stessa velocitÓ dalla cima di due torri distanti 50 piedi e alte rispettivamente 30 piedi e 40 piedi. Arrivano contemporaneamente al centro di una fonte che si trova fra le due torri. Quanto dista la fonte da ciascuna torre? (Leonardo Pisano, Liber Abaci, 1202) |
|

Filippo Calandri, Trattato d'Aritmetica, 1491
Tratta da banca dati Biblioteca Riccardiana - Firenze
La scala fra due torri
La scala deve essere fissata su un punto P del terreno equidistante delle
sommitÓ delle due torri.

Tale punto si pu˛ determinare individuando ad esempio la sua distanza
dalla base della torre A.
Chiamiamo dunque x la distanza fra P e la base della torre A
Allora (22 - x) sarÓ la distanza di P dalla base della torre B.
Quando la scala Ŕ appoggiata ad una torre, diventa l'ipotenusa di un
triangolo rettangolo che ha come cateti la torre stessa e il tratto di
terreno compreso fra la scala e la torre. La stessa cosa accade quando la
scala Ŕ appoggiata all'altra torre.
Si possono formare quindi due triangoli rettangoli che devono avere la stessa
ipotenusa, la qual cosa ci permette di scrivere l'equazione:
242 + x2 = 202 + (22-x)2
576 + x2 = 400 + 484 - 44x +x2
44x = 308
x = 7
La base della scala deve essere posta a 7 m dalla base della torre A.
Sempre il teorema di Pitagora ci permette di trovare l'altezza della scala,
che Ŕ 25 m.
La torre, il fossato e la scala
208,806 piedi
Scala e torre della stessa altezza
4 braccia
L'albero spezzato
34 braccia e 16 braccia
La canna appoggiata ad una parete
La torre, il fiume e la fune
50 braccia
Le due torri e la fonte
Tutto sta nel porre la distanza di una torre dalla fonte come incognita (x) e
scrivere un'equazione che uguagli le distanze (a & b) percorse dai 2
uccelli (perdonate il disegno avevo solo farfalle).

quindi per fare a = b scrivo (pensando alla diagonale del triangolo
rettangolo):
(80^2 + x^2) = [90^2 + (100 - x)^2]
Facendo 2 conti viene
x = 58,5
Quindi la torre alta 80 piedi dista 58,5 piedi , quella alta 90 piedi dista
41,5 piedi (cioŔ 100 - 58,5).
Le torri e i passeri
E' lo stesso del precedente.
30 al posto di 80
40 al posto di 90
50 al posto di 100
Risultato: 30 dista 32 e 40 dista 18 dalla fonte.
Inviato da Pam6203 al Forum il 15 settembre 2006
Base Cinque ha cortesemente dato la soluzione delle torri alte 20 e 24 metri,
distanti 22 metri tra di loro.Ma qualcuno ha provato a calcolare per torri da
30 e 14, distanti 8?
Possibile che occorra una scala molto pi¨ lunga della torre maggiore?
Attenzione.
Per mettervi sulla buona strada devo precisare che le unitÓ di misura del mio
quesito sono parasanghe (non metri ).
Ultimo aggiornamento: Luglio 2007
xhtml 1.1
Sito Web realizzato da Gianfranco Bo