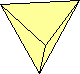
tetraedro
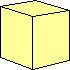
esaedro o cubo
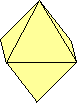
ottaedro
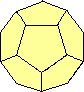
dodecaedro
icosaedro
[HOME - BASE Cinque - Appunti di Matematica ricreativa]
I poliedri regolari sono il punto d'arrivo degli Elementi
di Euclide e trovano la loro continuazione nei poliedri tronchi di Archimede.
In questo laboratorio di matematica ricreativa rappresentano invece il punto di
partenza per introdurre lo studio della geometria solida in 3° media.
Ecco 5 solidi particolari.
Volete imparare a costruirli con il cartoncino?

tetraedro |

esaedro o cubo |

ottaedro |

dodecaedro |

icosaedro |
Le fasi della costruzione del cubo
Ciascuna fase richiede e sviluppa abilità specifiche: tagliare, piegare,
incollare, risolvere problemi tecnici, essere precisi e avere una certa dose di
pazienza.
Si percepiranno con il tatto gli elementi principali dei poliedri: facce,
spigoli, vertici.
 1. Ritagliare |
 2. Piegare |
 3. Incollare |
 4. Perfezionare i particolari |

Ed ecco il risultato finale!

I cinque poliedri platonici in cartoncino
Il linguaggio dei poliedri
Ora è necessario indagare sulle proprietà dei solidi che abbiamo costruito
imparando le parole adatte a descrivere gli oggetti e le loro proprietà.

Definizione di poliedro
Un poliedro è un solido delimitato da un numero finito di poligoni
piani, detti facce del poliedro.
Definizioni di spigolo e vertice
In un poliedro ogni lato di ciascun poligono che costituisce una faccia
coincide con il lato di un'altra faccia e viene detto spigolo del
poliedro.
Ogni vertice di una faccia è vertice di altre facce (almeno 3) e si dice vertice
del poliedro.
Si dicono facce adiacenti del poliedro due facce che hanno uno spigolo
comune.
Due facce adiacenti formano un angolo che si chiama diedro.
Definizioni di poliedro convesso e poliedro concavo
In parole approssimative, un poliedro è concavo se ha delle rientranze, è
convesso se non ne ha.
Se vogliamo essere più "matematici", possiamo dire:
Un poliedro è convesso se ha le seguenti proprietà:
Altrimenti è concavo.
Definizione di vertice regolare
Consideriamo un vertice V di un poliedro e gli spigoli in esso incidenti; in
genere questi spigoli hanno lunghezze diverse e serve denotare con m la minima
di esse; prendiamo su ogni spigolo un punto che disti da V una lunghezza uguale
a m. Collegando questi punti otteniamo il "poligono associato al vertice":
se questo poligono è regolare si dice che V è un vertice regolare.

Ad esempio, nella figura qui sopra, V è un vertice regolare perché, presi VA = VB = VC, si ha che ABC è un poligono regolare (triangolo equilatero)
Definizione di poliedro regolare
Si dice poliedro regolare un poliedro le cui facce sono tutte
poligoni regolari e uguali e i cui vertici sono tutti dotati di poligoni
associati uguali e regolari, non necessariamente convessi.
Esistono 5 poliedri regolari convessi e 4 poliedri regolari concavi.
I solidi platonici
I solidi platonici, sono poliedri convessi le cui facce sono poligoni
convessi, regolari e uguali.
Esistono esattamente 5 poliedri di questo tipo: il tetraedro, il cubo,
l'ottaedro, il dodecaedro e l'icosaedro.
Le costruzioni dei cinque poliedri regolari sono dimostrate nel libro 13° e
ultimo degli Elementi di Euclide.
Le proprietà principali dei solidi platonici
I solidi platonici hanno le seguenti proprietà:
Contiamo le facce, gli spigoli e i vertici
| Solido | facce (F) | spigoli (S) | vertici (V) |
| tetraedro | 4 | 6 | 4 |
| cubo | 6 | 12 | 8 |
| ottaedro | 8 | 12 | 6 |
| dodecaedro | 12 | 30 | 20 |
| icosaedro | 20 | 30 | 12 |
La formula di Eulero
Osservando i dati della tabella, si ricava facilmente la seguente relazione:
V = S - F + 2
che è detta formula di Eulero, dal nome Leonard Euler, il grande
matematico svizzero del 1700.
Più in generale, la formula di Eulero afferma che per l'intera classe dei
poliedri convessi, ma anche per la più vasta gamma dei poliedri a superficie
semplicemente connessa (detto banalmente, quei poliedri che non presentano
"buchi" o "manici"), vale l'uguaglianza:
F - S + V = 2
Un metodo semplice per contare e calcolare facce, spigoli e vertici

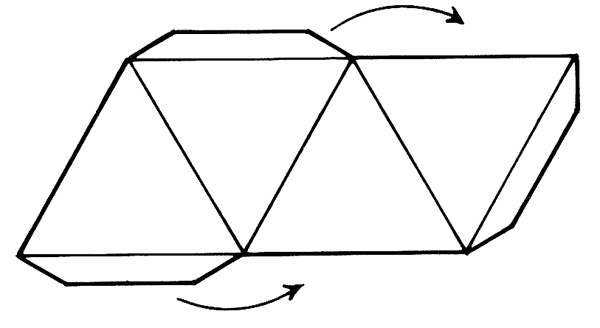
icosaedro |

un possibile sviluppo sul piano dell'icosaedro |
Consideriamo ad esempio l'icosaedro. Non è facile contare le facce, gli
spigoli e i vertici direttamente sul solido. Si corre il rischio di perdere il
conto o di dimenticare qualche elemento.
Se invece osserviamo lo sviluppo sul piano possiamo seguire tre fasi.
Una curiosità: i prefissi dei nomi dei poliedri
| num. facce | prefisso | num. facce | prefisso |
| 1 | mono | 16 | hexakaideca |
| 2 | di | 17 | heptakaideca |
| 3 | tri | 18 | octakaideca |
| 4 | tetra | 19 | enneakaideca |
| 5 | penta | 20 | icosa |
| 6 | hexa | 24 | icositetra |
| 7 | hepta | 30 | triconta |
| 8 | octa | 40 | tetraconta |
| 9 | ennea | 50 | pentaconta |
| 10 | deca | 60 | hexeconta |
| 11 | hendeca | 70 | heptaconta |
| 12 | dodeca | 80 | octaconta |
| 13 | triskaideca | 90 | enneaconta |
| 14 | tetrakaideca | 100 | hecato |
| 15 | pentakaideca |
Le idee di Platone sui cinque poliedri regolari
Il filosofo greco Platone utilizzò i 5 poliedri regolari convessi nel suo
libro intitolato Timeo, del 350 a.C., per spiegare il mondo naturale. Per
questo essi sono anche chiamati figure cosmiche.
Platone associò quattro poliedri a quelli che al suo tempo erano ritenuti i
quattro elementi fondamentali della natura, acqua, aria, terra, fuoco:
Il suo solido preferito era il dodecaedro del qual scrisse: “Restava una quinta combinazione e il Demiurgo (Dio) se ne giovò per decorare l’universo.”
La scoperta di questa figura risale almeno al VI sec. a. C., poiché oggetti a forma di dodecaedro appartenenti a quel periodo, sono stati rinvenuti in vari siti archeologici; i cristalli di pirite, che hanno forma dodecaedrica quasi perfetta, che si potevano rinvenire facilmente in molte zone della Magna Grecia, possono essere stati la fonte di ispirazione.
 Cristalli di pirite (ferro) in forma cubica |
 Cristalli di pirite (ferro) in forma dodecaedrica |
Griglie per la costruzione dei 5 poliedri regolari
Suggerimenti per l'uso (testati con Internet Explorer);
Salvate questa pagina sul vostro computer e scollegatevi da internet.
A questo punto avete varie scelte, ad esempio:
1) stampate la pagina, ritagliate le figure e fotocopiatele ingrandite su
cartoncino colorato; ingranditele in modo che ciascuna occupi interamente un
foglio di formato A4; io ho usato cartoncino per fotocopie da 140 gr;
Attenzione: se nella stampa le immagini risultano tagliate, cliccate su
File-Imposta pagina e impostate Orientamento Orizzontale.
2) fate una copia e incolla su Word (o altro elaboratore testi) e ingranditele in modo che occupino l'intera pagina; quindi stampatele su cartoncino colorato, meglio se con stampante laser;




settembre 2005
Sito Web realizzato da Gianfranco Bo