
[BASE Cinque - Appunti di Matematica ricreativa]
Il gioco delle 50 buste
(Inviato da Franco al Forum)
Siete stati selezionati per partecipare ad un nuovo programma in TV: “Il gioco delle 50 buste”.
Il gioco è molto semplice: di fronte a voi vi sono 50 buste che contengono cifre diverse e sconosciute (in particolare non avete la più pallida idea di quale sia l’importo massimo).
Dovete aprire una ad una le buste e di volta in volta decidere se accettare quella cifra e fermarvi oppure rifiutarla e passare alla busta successiva.
Alla fine la cifra è effettivamente vinta solo se è la più alta in assoluto fra tutte quelle delle 50 buste.
Qual è la migliore strategia per massimizzare la probabilità di vittoria?
La scelta del partner
(Inviato da Enrico Delfini al Forum)
La "dating strategy" si può descrivere più o meno in questo modo: immaginiamo uno scapolo che decida di voler mettere su famiglia. Si affida ad una agenzia di appuntamenti che gli garantisce, entro un anno, 10, o 20, o 50 incontri.
Dopo ogni serata, bisogna rispondere sì o no. Una volta detto no, non ci sono speranze di un ripensamento.
Primo appuntamento: sembra a posto, ma è verosimile che una delle prossime 49 sia meglio; "mi spiace cara, ma non se ne fa nulla..."
Ma non si può dire di no sempre: c'è il rischio di trovarsi con la scelta obbligata al 50° appuntamento (che è una racchia anche poco spiritosa!).
Quante scartarne quindi, prima di "scegliere la prima che è meglio della migliore vista finora"?
La risposta, non potendo tirare in ballo Fibonacci, la troviamo nell'onnipresente "e".
Variante alla scelta del partner
Il testo originale non parlava di giochi a premi ma di 100 fanciulle da
marito una delle quali sarebbe stata concessa a patto di riuscire a scegliere
quella con la dote (in senso economico $$$) più cospicua.
La carta più alta
(Inviato da Enrico Delfini al Forum)
Versione casalinga con le carte, e con 10 opzioni
Si mescolano le dieci carte di un seme
Se ne rivoltano un po'
Si continua fino a che una carta supera il valore maggiore visto.
Come prevedibile il risultato peggiore lo si ottiene rivoltando 0 carte o 9 carte: solo in un caso su dieci la scelta cadrà sulla carta davvero più alta. Voltandone 3, faremo la scelta migliore circa una volta su tre.
Sono gradite simulazioni.
L'algoritmo del parcheggio
Entri in un parcheggio nel quale si trova un dato numero di posti
auto liberi. I posti sono disposti casualmente e non sai dove si trovano.
Vuoi posteggiare in quello più comodo per te. Magari puoi scartare il primo,
magari anche il secondo, ma prima o poi devi sceglierne uno. Se scarti un
posto libero non puoi cambiare idea e tornare indietro.
Variante 1
Qual è la strategia migliore per massimizzare la speranza
matematica della comodità del parcheggio se ci sono n
ovvero 16 possibilità?
Variante 2
Qual è la strategia migliore per massimizzare la probabilità di
trovare il parcheggio più comodo se ci sono n ovvero 16
possibilità?
Nota: Il titolo di questa pagina, come quello dell'omonimo problema è tratto dal libro di Furio Honsell, L'algoritmo del parcheggio, Mondadori, 2007. A pagina 4 si legge: "L'autore devolverà i proventi della vendita di questo libro in beneficienza."
Il gioco delle 50 buste
(Soluzione inviata da Franco al Forum)
Visto che questo problema non ha avuto seguito e prima che passi definitivamente nel dimenticatoio posto la soluzione in allegato (non in chiaro così chi vuole può ancora cimentarsi):
Come già detto, ho trovato scritto (ma non mi sembra dimostrato) che, per N →∞, dovrebbe essere x = N/e e P = 1/e.
Se consideriamo che 50/e = 18,39 e che 1/e = 0,3679 ho motivo di pensare di aver ottenuto un risultato non disprezzabile (fra l’altro ho fatto qualche prova con N variabile e si vede che P diminuisce all’aumentare di N).
Tutto questo vale per il problema così come l'ho riformulato (si vince se trovi il massimo altrimenti niente).
Nota: il testo seguente è un'immagine in formato .gif

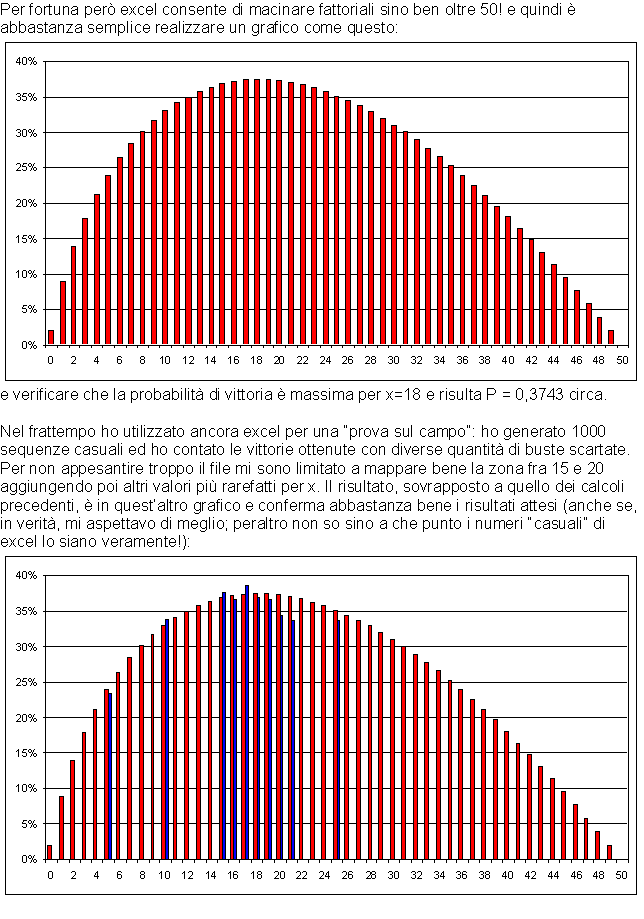
Ho provato a fare delle simulazioni anche con la precedente versione, nella quale si vinceva la busta scelta anche se non aveva la cifra massima.
In questo caso il criterio per massimizzare la vincita è lo stesso ma le buste da scartare all'inizio diminuiscono notevolmente; infatti se e vero che arrivando a 18 aumentano le probabilità di beccare quella con la cifra massima, aumentano anche le probabilità che il massimo sia fra le buste scartate e quindi che, dopo averle sfogliate inutilmente tutte, mi debba accontentare dell'ultima!
Non ho approfondito molto ma la vincita si massimizzava scartando circa
una decina di buste.
La scelta del partner
Variante alla scelta del partner
La carta più alta
L'algoritmo del parcheggio
Variante 1
Variante 2
Data creazione: novembre 2007
Ultimo aggiornamento: novembre 2007
xhtml 1.1
Sito Web realizzato da Gianfranco Bo