[HOME - BASE Cinque - Appunti di Matematica ricreativa]

Il Paradosso di Bertrand

Un particolare ringraziamento a Ivana Niccolai per questo contributo

Si tracci una corda a caso in un cerchio: qual e' la probabilità che essa sia più lunga del lato del triangolo equilatero inscritto?

(problema, di cui non è ancora stata pubblicata la risoluzione, proposto da Rocco Lupoi nel sito S.I.G. Giochi del Mensa Italia ).

L'enunciato del problema è ambiguo; non si può dare una risposta precisa se non viene espresso il significato di "tracciare una corda a caso", descrivendo il procedimento da seguire.

Infatti so che in base a determinati procedimenti nel tracciare la corda a caso, risultano ugualmente accettabili ben tre risposte distinte:

1)1/2

2)1/3

3)1/4

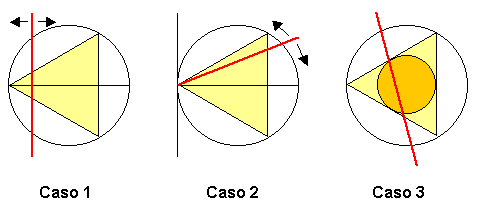
Prima risoluzione.
Tracciamo il diametro orizzontale e le corde perpendicolari a tale diametro, che passeranno per un punto che varia uniformemente lungo il diametro. Chiamo A il punto medio della base del triangolo equilatero inscritto (A giace,quindi, sul diametro) e B il punto del diametro, opposto ad A, che è la metà del raggio. Solamente quelle corde che tagliano il diametro fra A e B saranno più lunghe del lato del triangolo. Poiché il segmento AB è metà del diametro , la probabilità richiesta è 1/2.

Seconda risoluzione.
Chiamiamo A un punto della circonferenza (coincidente con un vertice del triangolo inscritto) e tracciamo una tangente al cerchio in A; l'altra estremità della corda varierà uniformemente sulla circonferenza generando una serie infinita di corde; solamente quelle corde che attraversano il triangolo sono più lunghe del lato del triangolo.
Poiché l'angolo del triangolo in A è di 60° e dato che le possibili corde giacciono tutte entro un campo di 180°, la probabilità di tracciare una corda più lunga del lato deve essere 60/180, cioè 1/3.

Terza risoluzione.
Nel triangolo equilatero inscritto, inscrivo un cerchio ; solamente le corde i cui centri giacciono entro il cerchio "più piccolo" sono più lunghe del lato del triangolo; poiché l'area del cerchio piccolo è proprio ¼ del cerchio grande, la probabilità richiesta è 1/4.

Insomma, i problemi inerenti alla "casualità" sono facilmente ambigui......

Risposte & riflessioni