[BASE Cinque - Appunti di Matematica ricreativa]
Parcheggio selvaggio
(Inviato da Franco al Forum)
Una via Ŕ lunga a sufficienza da consentire il parcheggio esattamente a 4 auto.
Gli automobilisti per˛ hanno la brutta abitudine di parcheggiare in maniera assolutamente casuale, senza interessarsi minimamente del fatto che qualcun altro voglia fare altrettanto (ma anche senza impegnarsi ad impedirlo).
Qual'Ŕ il valore atteso del numero di auto che trovano parcheggio nella via?
Naturalmente si considerino le auto tutte di uguale lunghezza e si ipotizzi pure che non occorra alcuno spazio per le manovre
Parcheggio selvaggio
(Soluzione inviata da Sancho Panza al Forum)
I posti auto disponibili sono 4, dunque ci sono solo 3 casi possibili:
A) La prima auto Ŕ parcheggiata tra il primo e il secondo posto
B) La prima auto Ŕ parcheggiata tra il secondo e il terzo posto
C) La prima auto Ŕ parcheggiata tra il terzo e il quarto posto
(Infatti la probabilitÓ che la prima auto sia parcheggiata esattamente su uno solo dei 4 posti disponibili Ŕ uguale a zero).
Nel caso B) resta un posto libero a destra e uno a sinistra. Totale: 3 auto parcheggiate
Nel caso A) e nel caso C)
da un lato non resta posto libero per un'altra auto;
mentre dall'altro lato, il posto libero Ŕ uguale a (2 + x) con x che varia da 0 a 1, quindi lo spazio tra la prima macchina parcheggiata e la seconda varierÓ in modo uniforme tra 0 e (1 + x)
Se lo spazio tra le due macchine Ŕ minore di x, vi Ŕ lo spazio per parcheggiare una terza macchina a destra o a sinistra; se lo spazio tra le due macchine Ŕ maggiore di 1, vi Ŕ lo spazio per parcheggiare una terza macchina tra le prime due.
Quindi, la probabilitÓ che la seconda macchina lasci lo spazio libero per una terza macchina Ŕ:
2x / (1+x)
Siccome x varia in modo uniforme tra 0 e 1, devo calcolare:
La probabilitÓ che ci stiano solo 2 macchine sarÓ quindi:
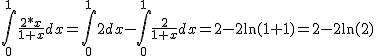
Numero medio di auto parcheggiate:
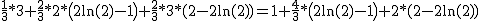
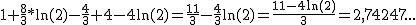
Data creazione: novembre 2007
Ultimo aggiornamento: novembre 2007
xhtml 1.1
Sito Web realizzato da Gianfranco Bo