[BASE Cinque - Appunti di Matematica ricreativa]

Il problema del collezionista (coupon collector's problem)

Avete mai completato un album di figurine?

All'inizio la collezione si riempie facilmente ma poi diventa sempre più difficile trovare nuove figurine. Infine, trovare l'ultima figurina mancante per completare l'album è un'impresa molto costosa!

Da questa situazione prende il problema del collezionista: quante figurine si devono comprare per completare l'album?

Cerchiamo di risolverlo partendo da alcuni casi più semplici.

1. Lancio della moneta

Quante volte, in media, si deve lanciare una moneta per ottenere almeno una testa e una croce?

2. Lancio del dado

Quante volte, in media, si deve lanciare un dado (a 6 facce) per ottenere tutti i numeri?

3. L'album di figurine

Quante figurine, in media, si devono comprare per completare un album di 100 figurine?
Le figurine si comprano una alla volta. Ogni figurina è chiusa in una busta, di cui non si può vedere il contenuto. Ogni busta contiene una figurina scelta a caso fra le 100 che compongono l'album. Le figurine sono tutte equiprobabili, cioè ogni figurina ha probabilità 1/100 di trovarsi in una busta.

4.Generalizziamo

Quante figurine, in media, si devono comprare per completare un album di n figurine diverse?

Le condizioni sono quelle descritte nel problema precedente.

Risposte & riflessioni

ATTENZIONE: appunti da completare.

Il numero atteso (o medio) di prove

Per risolvere in modo semplice il problema del collezionista è bene capire il concetto di numero atteso (o medio) di prove da fare perché un certo evento si verifichi.

Se un evento ha probabilità p, allora si verifica in media ogni 1/p prove.
Perciò il numero atteso di prove è 1/p.

Si parla anche di "tempo di attesa".

1. Lancio della moneta

Quante volte, in media, si deve lanciare una moneta per ottenere almeno una testa e una croce?

• Al primo lancio esce una delle facce (con probabilità 1).
• Quanti lanci devo ancora fare per ottenere l'altra faccia?
  La probabilità che esca tale faccia è p=1/2 perciò il numero atteso di prove per ottenerla è n=1/p=2.

In conclusione, per ottenere tutte le facce della moneta occorre 1 lancio per la prima e in media altri 2 lanci per la seconda:

n=1+2=3 lanci

2. Lancio del dado

Quante volte, in media, si deve lanciare un dado (a 6 facce) per ottenere tutti i numeri?

• Al primo lancio esce una delle facce (con probabilità 6/6=1).
• Quanti lanci devo ancora fare per ottenere una delle rimanenti 5 facce?
  La probabilità che esca una faccia diversa dalla prima è p=5/6, perciò il numero atteso di prove per ottenerla è:
  n=1/p=1/5/6=6/5 lanci
• Quanti lanci devo ancora fare per ottenere una delle rimanenti 4 facce?
  La probabilità che esca una faccia diversa dalle due già uscite è p=4/6, perciò il numero atteso di prove per ottenerla è:
  n=1/p=1/4/6=6/4 lanci
• Allo stesso modo, per ottenere la quarta faccia occorrono ancora:
  n=6/3 lanci
• Per ottenere la quinta faccia occorrono ancora:
  n=6/2 lanci
• Quanti lanci devo ancora fare per ottenere l'ultima faccia?
  La probabilità che esca una faccia diversa dalle 5 già uscite è p=1/6 perciò il numero atteso di prove per ottenerla è:
  n=1/p=1/1/6=6 lanci

In conclusione, per ottenere tutte le facce del dado occorre fare in media:

n=6/6+6/5+6/4+6/3+6/2+6/1=14,7 lanci

Cominciamo a capire che la formula generale sarà una sommatoria.

3. L'album di figurine

Quante figurine, in media, si devono comprare per completare un album di 100 figurine diverse?
Le figurine si comprano una alla volta. Ogni figurina è chiusa in una busta, di cui non si può vedere il contenuto. Ogni busta contiene una figurina scelta a caso fra le 100 che compongono l'album. Le figurine sono tutte equiprobabili, cioè ogni figurina ha probabilità 1/100 di trovarsi in una busta.

• Al primo acquisto ottengo una nuova figurina (con probabilità 1).
• Quanti acquisti devo ancora fare per ottenere un'altra delle rimanenti 99 figurine?
  La probabilità che esca tale figurina è p=99/100 perciò il numero atteso di prove per ottenerla è n=100/99.
• ... e così via, 100/98, 100/97, ... fino all'ultima figurina...
• Quanti acquisti devo ancora fare per ottenere la rimanente ultima figurina?
  La probabilità che esca tale figurina è p=1/100 perciò il numero atteso di prove per ottenerla è n=1/p=100 acquisti.

In conclusione, per ottenere tutte le figurine della collezione occorre fare in media:

n=100/100+100/99+100/98+100/97+...+100/1=518,7 circa acquisti

In formula:

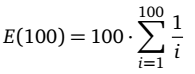
E(100) indica il numero atteso (Expected) di acquisti da fare per ottenere 100 figurine

4.Generalizziamo

Quante figurine, in media, si devono comprare per completare un album di n figurine diverse?

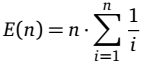
E(n) indica il numero atteso (Expected) di acquisti da fare per ottenere n figurine

Per dimostrarlo supponiamo di avere già raccolto i figurine diverse e chiediamoci quante ne dobbiamo comprare per averne una in più, cioè i+1.

La figurina che vorremmo trovare è una delle (n-i) che mancano alla nostra collezione.

La probabilità di trovarla in un acquisto è:

p=(n-i)/n

quindi il numero atteso di acquisti da fare per trovarla é:

numero acquisti=n/(n-i)

Una formula ricorsiva

Dalla formula:

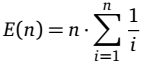
si ricava:

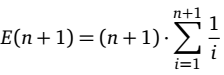
e  da quest'ultima, si ricava la formula ricorsiva:

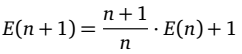
che può essere utile per calcolare i successivi valori di E(n).

---

Pace e bene a tutti.

GfBo

Data creazione: aprile 2020

Ultimo aggiornamento: aprile 2020

html5

Sito Web realizzato da Gianfranco Bo