[HOME - BASE Cinque - Appunti di Matematica ricreativa]
di Andrea Becucci
1. Come si fa
1.1 per le moltiplicazioni
1.2 per le divisioni intere
1.3 per le divisioni con resto
2. Significato della prova
Classi di resto modulo 9
3. Perché "del 9"?
Proprietà del numero 9 nel nostro sistema di numerazione
La finalità della prova del 9 è quella di
controllare l'esatezza di una moltiplicazione tra numeri...
"grandi", quando i calcoli sono fatti a mano.
Se la prova dà esito negativo, abbiamo sbagliato i calcoli
ed occorre rivederli nella moltiplicazione, se dà esito
positivo però non ci dà la certezza di avere in mano un
risultato corretto: il nostro risultato è corretto a meno di
un multiplo di 9.
Considerato che sbagliare di un multiplo di 9 una
moltiplicazione è abbastanza difficile, diciamo che quando
la prova torna, siamo abbastanza sicuri che quello calcolato
da noi sia il risultato corretto.
Passiamo ad analizzare come si fa.
Calcolo della prova del 9 per le
moltiplicazioni
Iniziamo a vedere come si fa con un esempio
59.714 * 24.339 = 1.453.379.046
Sarà corretto il risultato o no? Facciamo la prova del 9.
Si traccia una croce e la
riempiamo con i seguenti numeri:
In alto a sinistra: si sommano le cifre del primo fattore (5+9+7+1+4=26)
ripetutamente, finché non resta un numero ad una sola cifra
(2+6=8)
| 8 | |
In alto a destra facciamo lo stesso procedimento con il
secondo fattore (2+4+3+3+9=21 2+1+=3)
| 8 | 3 |
In basso a sinistra: si
moltiplicano i 2 numeri in alto sulla croce, e si riduce il
risultato ad una sola cifra, sommandone le cifre (3*8=24 2+4=6)
| 8 | 3 |
| 6 |
Infine in basso a destra
mettiamo la somma delle cifre del numero che noi crediamo sia
il risultato dell'operazione (1+4+5+3+3+7+9+0+4+6=42 4+2=6)
| 8 | 3 |
| 6 | 6 |
Se i due numeri in basso sono
uguali la prova ha esito positivo, altrimenti ha esito
negativo.
Ricordiamo che se la prova ha esito negativo, la
moltiplicazione è sicuramente errata, mentre se ha esito
positivo, il risultato trovato da noi potrebbe differire dal
risultato reale per un multiplo di 9.
Riepiloghiamo:
| Somma
cifre primo fattore |
Somma
cifre secondo fattore |
| Somma
cifre prodotto dei 2 numeri in alto |
Somma
cifre risultato "ipotetico" |
Calcolo della prova
del 9 per le divisioni intere
Dal momento che dividendo : divisore = quoziente
Segue che divisore * quoziente = dividendo
Per cui abbiamo:
| Somma
cifre divisore |
Somma
cifre quoziente |
| Somma
cifre prodotto dei 2 numeri in alto |
Somma
cifre dividendo |
Calcolo della prova
del 9 per le divisioni con resto
Dal momento che dividendo : divisore = quoziente con resto
non 0
Segue che divisore * quoziente + resto = dividendo
Per cui abbiamo:
| Somma
cifre divisore |
Somma
cifre quoziente |
| Somma
cifre prodotto dei 2 numeri in alto + somma cifre resto |
Somma
cifre dividendo |
Urge un esempio:
732 : 17 = 43 con resto 1
| 17 1+7 8 |
43 4+3 7 |
| 7*8=56 5+6=11 1+1=2 Dunque 2 è la somma delle cifre del prodotto tra i 2 numeri in alto; a questa bisogna aggiungere il resto (1), per cui il calcolo non è ancora finito. 2+1=3
|
7+3+2=12 1+2=3 3 |
Significato della prova del 9 per le
moltiplicazioni
Per capire bene cosa facciamo quando facciamo la
prova del 9, bisogna introdurre la "matematica
dell'orologio", ovvero le classi di resto.
I numeri naturali siamo abituati a figurarceli disposti su
una semiretta orientata. Possiamo immaginare di avere in mano
un gran cesto contenente tutti i numeri naturali (lo so che
sono infiniti, ma immaginiamocelo lo stesso) e di lasciare lo
0 alla partenza e, ad ogni passo che muoviamo sulla
semiretta, lasciare il numero successivo (l'1 al primo passo,
il 2 al secondo e così via.
Avremo perciò una situazione del genere:
|----|-----|-----|-----|----|-----|-----|-----|-----|----|-----|------|---------->
0.. 1... 2.... 3.... 4.... 5... 6... 7.... 8.... 9.. 10.. 11..
12 ...
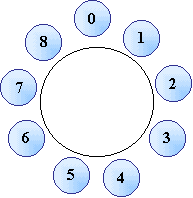
Divertiamoci a cambiare un pochino lo scenario.
Seminiamo i numeri anziché su una semiretta su un cerchio
sul quale ci sono 9 scatole capienti. Nella prima scatola ci
lasciamo lo 0, nella seconda l'1 e così via fino a mettere
l'8 nella nona ed ultima scatola; poi continuiamo a "deporre"
i numeri sempre girando in senso orario, per cui mettiamo il
9 nella scatola dove c'era già lo 0, il 10 dove c'è l'1,
ecc..
Avremo perciò una situazione del genere:

Vediamo che cambiando scenario e passando dal
seminare i numeri su una semiretta al seminarli su una linea
chiusa, abbiamo raggruppato tutti i numeri in varie scatole:
per capirsi di ogni scatola eleggiamo un "rappresentante",
un "capo-squadra" che per semplicità sarà di ogni
scatola il numero più piccolo.
Che cosa abbiamo nelle varie scatole?
Nella scatola dello 0 abbiamo i seguenti numeri: 0, 9, 18, 27,
36, 45, 54, 63, ...
Nella scatola dell'1 abbiamo: 1, 10, 19, 28, 37, 46, 55, 64,
...
Nella scatola del 2: 2, 11, 20, 29, 38, 47, 56, 65, ...
.
.
.
Nella scatola dell'8: 8, 17, 26, 35, 44, 53, 62, 71, ...
Un po' di osservazioni sui numeri contenuti nelle varie
scatole (si potrebbe pensare di farlo fare ai bimbi: una
sorta di scoperta guidata).
Nella scatola dello 0 ci sono i multipli di 9, ovvero tutti
quei numeri che divisi per 9 danno resto = 0. Importante
soffermarsi sul resto; in genere nella divisione siamo molto
più interessati a conoscere il quoziente, mentre il resto è
spesso una scomoda appendice. In questa specie di gioco con
regole cambiate, noi ce ne infischieremo dei quozienti, ma
saremo attentissimi al resto.
Nella scatola dell'1 ci sono tutti i numeri che divisi per 9
danno resto 1.
E così via.
Presa una scatola a caso e presi 2 numeri a caso da essa, la
differenza tra questi 2 numeri sarà sempre un multiplo di 9.
Presa una scatola a caso e pescato a caso un numero, la somma
(eventualmente ripetuta) delle sue cifre darà il numero
rappresentante della scatola, con la sola eccezione della
scatola dello 0, in cui tutti i numeri (0 escluso) danno per
somma 9.
Ed ora l'addizione.
Come si fa 3+2 sulla semiretta?
Si parte dall'origine e si cammina di tanti passi quanto
indicati dal primo addendo; poi ci si muove ancora del numero
di passi indicati dal secondo addendo. Alla fine ci si ferma,
alziamo gli occhi sul "cartello" che ci indica (in
buona sostanza) quanti passi ci siamo allontanati
dall'origine.
|----|-----|-----|-----|----|-----|-----|-----|-----|----|-----|------|---------->
0 ................3.......... 5
....................|----2----|
Nella matematica dell'orologio, il meccanismo è il solito:
partenza dall'origine (scatola dello 0), si fanno 3 passi in
senso orario e poi altri 2 e si guarda dove si arriva. Anche
qui si arriva al 5.

Benissimo e come la mettiamo con 7 + 5?
La mettiamo sempre uguale, anche se il risultato potrebbe
spaventarci.
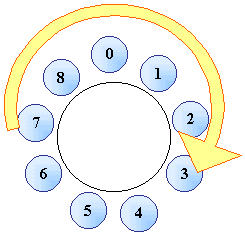
Dunque 7+5=3??? In effetti, girando in tondo
e camminando di 7 + 5 = 12 passi ci siamo allontanati da
"casa" soltanto di 3 passi; poco importa se abbiamo
compiuto un giro completo, questo per noi è ininfluente,
l'importante è stabilire dove siamo andati a cascare. Ma
visto che "normalmente" 7 + 5 = 12, chiediamoci in
quale scatola si trova il numero 12? Ma in quella di cui il 3
è degno rappresentante (ricordiamoci dell'osservazione sulla
somma dele cifre dei numeri di ogni scatola). Ecco che allora
in qualche modo le cose cominciano ad avere un senso.
Che cosa abbiamo imparato da tutto ciò?
Sommando ripetutamente le cifre di un numero scritto nel
nostro sistema di numerazione, fino a ridurlo ad un numero di
una cifra soltanto, otteniamo il resto di quel numero nella
sua divisione per 9 (eccezion fatta per i multipli di 9 per i
quali otteniamo 9 anziché 0).
Conclusione. Che cosa facciamo quando facciamo la prova del 9?
Calcoliamo il resto della divisione per 9 del primo fattore,
il resto della divisione per 9 del secondo fattore,
moltiplichiamo questi 2 numeri e sommando le cifre del
risultato, otteniamo il resto della divisione per 9 che il
risultato corretto deve avere. Poi calcoliamo il resto della
divisione per 9 del risultato che abbiamo calcolato noi.
Giusta dunque la conclusione che se questi 2 numeri sono
diversi, la moltiplicazione è errata, mentre se i numeri
sono uguali, la prova ci dice soltanto che hanno lo stesso
resto nella divisione per 9, ovvero differiscono tra loro per
un multiplo di 9, che noi speriamo ardentemente essere lo 0.
Perché "del 9"?
Abbiamo già notato che la somma delle cifre di un
qualsiasi numero dia come risultato il suo resto nella
divisione per 9. Ciò avviene perché nel nostro sistema di
numerazione, 9 è il maggiore tra i numeri che si possono
scrivere con una cifra soltanto.
Si può osservare che la divisione di 10 per 9 dà resto 1 (10=9+1
e 9 è divisibile per 9) e così la divisione di 100 per 9 (100=99+1
e 99 è divisibile per 9), di 1000 per 9 (1000=999+1), e così
via. La somma delle cifre di 10, 100, 1000, è ovviamente 1.
Ma succede sempre anche che 20, 200, 2000, ecc, hanno resto 2
nella divisione per 9? Certamente, visto che 20:9=(10+10):9=10:9+10:9
e così abbiamo resto 1 dal primo addendo, resto 1 dal
secondo e il resto complessivo è proprio 1+1=2.
Dunque stesso discorso per 30, 300, 3000, ..eccetera,
eccetera.
Conclusione preso un qualunque numero, possiamo determinare
il suo resto nella divisione per 9 semplicemente sommando le
sue cifre.
Esempio: 7483=7000+400+80+3.
Per quanto osservato sopra abbiamo resto 7 dal primo addendo,
4 dal secondo, 8 dal terzo e 3 dall'ultimo: 7+4+8+3=22. Ma un
numero diviso 9 non può avere un resto maggiore di 9; questi
22 oggetti che mi sono rimasti devono ancora essere divisi
per 9 e così potrò vedere quanti me ne restano. Ma allora,
per determinare il resto di 22 per 9 posso sommare le cifre:
2+2=4 e questo è il resto sia di 22 sia di 7483 nella
divisione per 9.
La prova del 9 dunque viene fatta perché è molto semplice
determinare il resto della divisione di un numero per 9 (basta
sommare le sue cifre ripetutamente finché non resta un
numero ad una sola cifra), in più "sbagliare" di
un multiplo di 9 è cosa abbastanza rara.
Fare la prova dell'8 o del 7 sarebbe estremamente più lungo
e complesso, che il gioco non varrebbe la candela.
Sito Web realizzato da Gianfranco Bo