[HOME - BASE Cinque - Appunti di Matematica ricreativa]
Ricreazioni di Dicembre 2002
![]()
300. L'isola dei cornuti, alternativa
di Marco M.
Carino il quiz dell'isola dei
cornuti. Vi propongo un'alternativa: supponiamo che di
cornuto ve ne sia uno solo (il sottoscritto, ovviamente) e
decida di perdonare la propria moglie, non gettandola di
sotto. Secondo voi cosa succederebbe?
>>> Risposte & riflessioni
Marco M.
Esatto! Tutte le mogli verrebbero gettate di sotto! (Cosa che
avrei fatto personalmente, tanto per far vivere con il
rimorso d'aver ucciso la propria moglie innocente il/i
gentiluomo/ini che mi fecero becco)
Nel caso in cui non vi fosse chiaro il perché tutte le mogli
verrebbero gettate, contattatemi pure :o)
![]()
299. Quanti quadrati?
di Peppe
Quanti sono i QUADRATI in questa figura?

>>> Risposte & riflessioni
Peppe
Contiamo i centri di simmetria di ciascun quadrato.
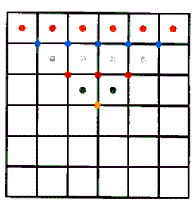
I quadrati sono:
36 da 1 quadretto
25 da 4 quadretti
16 da 9 quadretti
9 da 16 quadretti
4 da 25 quadretti
1 da 36 quadretti
Totale = 91 quadrati
![]()
298. I sette ponti di Konisberg
di Peppe
Sul fiume Pregel a Kónisberg ci sono due isole
collegate da sette ponti secondo questo schema:Si racconta
che i cittadini cercassero un percorso per fare tutta la
passeggiata dei ponti senza passare per due volte per lo
stesso ponte e senza saltarne alcuno. Il matematico Leonhard
Euler risolse il problema, stabilendo un teorema sulla
percorribilità di un grafo. Qual è il percorso?

>>> Risposte & riflessioni
Peppe
Nel 1736 il matematico svizzero Leonhard Euler provò che è
impossibile trovare un percorso che passi una sola volta su
ciascun ponte. Il problema può essere schematizzato con un
grafo come quello qui a fianco.Poiché tutti i nodi sono di
grado dispari (ogni regione è infatti collegata alle altre
da un numero dispari di ponti: 3 o 5) non è possibile:- ne
un percorso chiuso (che torna cioè al punto da cui si è
partiti) per il quale occorre che tutti i nodi siano di grado
pari (si può uscire da un nodo in cui si è entrati);- ne un
percorso aperto (che non torna cioè al punto di partenza)
per il quale è necessario che due nodi siano di grado
dispari, mentre tutti gli altri di grado pari (i primi due
saranno i nodi di partenza e di arrivo, mentre da tutti gli
altri si può uscire una volta entrati).

![]()
297. La lettera E
di Peppe
La lettera E della figura è composta da 10
quadretti.E' possibile tagliarla in 5 pezzi che, senza
ribaltarli, possono essere disposti in modo da formare un
quadrato.
In che modo?

>>> Risposte & riflessioni
Peppe
Il quadrato formato dai pezzi che compongono E deve avere il
lato lungo Radq(10).
Otteniamo tale lunghezza prendendo l'ipotenusa del triangolo
rettangolo i cui cateti misurano rispettivamente 3 e 1.

![]()
296. Tangram
di Peppe
E' un antichissimo gioco cinese formato da 7
tasselli (5 triangoli isosceli,1 quadrato e 1 parallelogramma)
che,opportunamente disposti,compongono il quadrato a lato.
Spostando, ruotando e ribaltando i tasselli si possono
formare un gran numero di figure, come ad esempio, il
telefono, il gatto ecc.
Con i tasselli del TANGRAM puoi ottenere dei poligoni
convessi. Prova a scoprire come ottenere un TRIANGOLO, un
QUADRILATERO, un POLIGONO con 5 lati e un POLIGONO con 6 lati.

>>> Risposte & riflessioni
Peppe
Con i 7 pezzi del tangram siPossono comporre
esattamente 13 diversi poligoni convessi(senza considerare i
loro ribaltamenti e le loro rotazioni).

![]()
295. Cicli di Langford
di Giofulmine
In una griglia di 5x4 mettiamo all'esterno i numeri
da 1 a 7, a coppie, come nella figura sotto:
1 4 5 3 6
7 7
1 2
6 4 2 5 3
Come si vede, leggendo in senso orario, data la coppia (h, h)
tra il primo e il secondo numero h ci sono sempre h numeri.
Per esempio, tra 1 e 1 c'è 7; tra 2 e 2 ci sono 3 e 5; tra 3
e 3 ci sono 6, 7 e 2; ecc. Chiamiamo (h,H,h) tale proprietà.
Proviamo a tagliare in qualche punto il ciclo e scriviamo i
14 numeri linearmente, p.es.:
1 4 5 3 6 7 2 3 5 2 4 6 1 7
Qui non vale (h,H,h) perché tra 1 e 1 ci sono 11 numeri
invece di uno. Provando tutte la possibili diverse partenze,
vediamo che solo:
5 3 6 7 2 3 5 2 4 6 1 7 1 4
gode della proprietà (h,H,h). Allora la figura iniziale
definisce un ciclo-uno di Langford. Se avessimo trovato m
partenze diverse, avremmo avuto un ciclo-m; ogni ciclo-m
fornisce m soluzioni al famoso problema di Langford. Vedere
su Internet il sito
http://www.lclark.edu/~miller/langford.html
Si abbia ora il ciclo:
3 7 2 4 6
2 1
5 5
6 3 7 4 1
Questo è un ciclo-zero di Langford perché vale (h,H,h) ma
non è sviluppabile linearmente. Sapendo che se due cicli
differiscono solo per il senso di rotazione sono considerati
un ciclo solo, trovare l'altro ciclo-zero.
>>> Risposte & riflessioni
Giofulmine
1 5 4 6 3 7 2 5 3 2 6 4 1 7
![]()
294. Tre quadrati all'interno di
un triangolo
di ...
So che oltre al triangolo equilatero, c'è un'unica
altra forma di triangolo, grazie alla quale si possono
sistemare all'interno tre quadrati uguali di dimensione
massima.
In tale triangolo qual è il rapporto tra il lato più lungo
e gli altri due?
>>> Risposte & riflessioni
Dino e Ivana

![]()
293. Corde
di Peppe
Una corda divide un cerchio in due regioni.
2 corde lo dividono in almeno 3 regioni; se si intersecano,
ne delimitano 4.
3 corde delimitano almeno 4 regioni; se si intersecano tutte
in punti diversi allora 3 corde delimitano 7 regioni.

Il numero di regioni è massimo quando considerando una nuova corda questa taglia tutte le precedenti senza che per un suo punto ne passi più di una.
Qual'è il numero massimo di regioni delimitato da 5 corde? E da 10 ? E da 7 corde ?
>>> Risposte & riflessioni
Peppe
L'n-esima corda tracciata risulta divisa in n segmenti
delimitati dalle n-1 corde precedenti e dai suoi due estremi.
Ognuno di questi segmenti taglia una delle regioni precedenti
in due e determina una nuova regione.
L'n-esima corda aggiunge n regioni al totale. Poiché 0
corde danno una regione, 5 corde danno al massimo:
1+1+2+3+4 +5=16.
In generale n corde danno:
1 +1 +2 +3 +....+ n
che si scrive:
(n2 + n + 2) / 2
Per n = 10 si hanno 56 regioni.
![]()
292. Numeri vicini e lontani
di Peppe
Lo schema qui sopra riprodotto è formato da cerchi
e da tratti che li uniscono tra loro. In questo schema si
devono disporre le cifre da 1 a 8 in modo tale che:
a) in ogni cerchio ci sia una delle cifre;
b) nei cerchi connessi tra loro da tratti non ci siano due
cifre contigue nella successione numerica.
Per esempio, se metto 4 nel cerchio a destra, in quelli
successivi a sinistra non potrò mettere (perché connessi
con il primo) nè il 3, nè il 5.

>>> Risposte & riflessioni
Peppe
Ecco la soluzione a schema riempito. Essa è unica,
e la sola via logica per ottenerla consiste nel comprendere
che l'1 e l'8 vanno posti nei cerchi centrali perché essi
sono i due soli numeri, nella successione data, che
posseggono un solo numero adiacente (rispettivamente il 2 e
il 7). Una volta giunti a questo punto la soluzione diviene
piuttosto semplice da reperire.

![]()
291. Collegamenti
di Peppe
2 punti sono collegati da 1 linea
0------------------0
3 punti da 3 linee

4 punti da 6 linee

Volendo collegare ogni punto a tutti gli altri, quante linee sono necessarie per collegare 5 punti? E quante per collegare 10 punti? E quante per n punti?
>>> Risposte & riflessioni
Peppe
Se vi sono n punti ognuno deve essere collegato a tutti gli
altri e per ogni punto vi sono (n-1) linee.
I collegamenti tra gli n punti sono perciò n * (n-1).
Tale numero va però diviso per 2 perché ogni linea è
contata due volte.
La formula che esprime il termine generale della successione
è:
an = (n * (n-1))/2
Quindi, 5 punti sono collegati da 10 linee, mentre 10 punti sono collegati da 45 linee.
Sito Web realizzato da Gianfranco Bo