[HOME - BASE Cinque - Appunti di Matematica ricreativa]
Ricreazioni di Luglio 2002
![]()
250. Il mistero di Vega
di Enrico Delfini
Faccio questa domanda a Giorgio Dendi perchè mi
pare di ricordare che lavora in banca, e che vive in Friuli.
Se le premesse sono vere, è probabile che abbia, o abbia
avuto, fra le mani la banconota da 50 talleri sloveni.

Scansione inviata da Peppe
Sulla banconota in questione è effigiato
Jurij Vega (1734-1802), che penso sia un matematico sloveno.
Sulla sinistra è riprodotta una figura geometrica (un
cerchio con raggi e segmenti vari di corde varie.
Non riesco a decifrare il concetto o teorema sottostante alla
figura.
Caro G.D., tu ne sai qualcosa?
Enrico
>>> Risposte & riflessioni
Per quanto riguarda la banconota con
effigiato Vega, introvabile nelle biblioteche e nelle
librerie, abbiamo scritto alla Società Numismatica Slovena,
e al sig. Andrei Novak, che ci hanno gentilmente fornito l'e-mail
del progettista della banconota sig.Miljenko Licul (lo
abbiamo contattato e stiamo aspettando una risposta)e hanno
detto che .il cerchio situato sul lato sinistro della
banconota da 50 talleri slovena, è una riproduzione di una
progettazione dal trattato di Vega sulla sfera che diviene
piatta sui suoi poli. Questo fenomeno, che è osservabile
anche nel caso della terra, è stato spiegato da Vega
matematicamente.
Comunque ti allego la lettera in inglese che abbiamo ricevuto.
Thank you for your e-mail letter of August 14th, 2002 in
which you explained that you are interested in banknote for
50 SIT.
The circle that you are curious about, located on the left
side of a 50 SIT banknote, is a reproduction of a design from
Vega's treatise on the sphere turning on its vertical axle
and getting flat on its poles. This phenomenon, which is also
observable in the case of the Earth, was explained by Vega
mathematically. The horizontal axle contains a protective
component in the form of micro-text composed of the name Bank
of Slovenia, numerical indication of value and shortened
designation of currency.
For further information on the topic you can contact Mr.
Miljenko Licul at e-mail address:
irena.l@studio-zodiak.si
You are invited to obtain more information about Slovenian
currency at the Internet address:
" http://www.bsi.si/html/eng/banknotes_coins/index.html"
For any additional numismatics issues about Slovenian
banknotes and coins, please contact:
Numizmaticno drustvo Slovenije (Slovenian Numismatic Society)
Ilirska ulica 14
SI-1000 Ljubljana, Slovenija
(e-mail address: "numdruslo@yahoo.com"
check the web-site "http.//www.angelfire.com/nd/numismatdrslo").
We hope that the above information will be useful to you.
Sincerely yours,
Andrej Novak dr. Brane Bertoncelj
Banknote Department
![]()
249. Al ballo del sabato sera
di Alessandro89
Al ballo di sabato scorso hanno partecipato 53
persone tra uomini e donne. Durante la serata una donna ha
ballato con 10 uomini, un'altra con 11, un'altra con 12, e
così via fino all'ultima che ha ballato con tutti gli uomini
presenti. Quante donne hanno partecipato alla festa?
>>> Risposte & riflessioni
Jack202
1 donna ha ballato con 10 uomini, dunque c'erano
almeno 1 donna e 10 uomini
1 altra ha ballato con 11 uomini, dunque c'erano almeno
2 donne e 11uomini
1 altra ha ballato con 12 uomini, dunque c'erano almeno
3 donne e 12uomini
...
C'erano dunque (x) donne e (9+x) uomini, in totale 53 persone
9 + 2x = 53 --> x=22
C'erano 22 donne e 31 uomini.
Dino e Ivana Niccolai
Le donne che hanno preso parte alla festa sono state
in 22.
Dette, infatti, d le donne presenti alla festa ed u gli
uomini, poichè dev'essere:
u - d = 9
abbiamo anzitutto:
u = 9 + d
Inoltre il totale dei partecipanti è stato:
u + d = 53
e sostituendo il valore di u trovato si ha subito:
9 + d + d = 53
ossia d = 22. Di conseguenza gli uomini intervenuti sono stati in:
u = 9 + d = 9 + 22 = 31
![]()
248. Travasi indeterminati
di Alessandro89
Abbiamo un recipiente contenente 2N litri d'acqua, e
due recipienti più piccoli di M e 2N-M litri rispettivamente.
Come possiamo dividere l'acqua in due parti uguali da N litri
ciascuna, potendo solo fare travasi da un recipiente
all'altro?
>>> Risposte & riflessioni
Risposta in sintesi tratta dalle FAQ
di it.hobby.enigmi di Mariano Tomatis
Il problema si risolve se N ed M sono primi tra
loro, e la soluzione (non necessariamente la piu` breve)
ricorda gli algoritmi di divisibilita`. Supponiamo per
comodita` M < N per sapere qual e` il recipiente piu`
piccolo. Versiamo acqua dal recipiente grande al piccolo fino
a riempirlo, e a questo punto travasiamo l'acqua nel
recipiente medio. Se a un certo punto esso ha N litri, siamo
a posto; altrimenti prima o poi si riempie. Allora versiamo
l'acqua dal medio al grande, e finiamo di travasare dal
piccolo al medio. La situazione e` simile a quella iniziale,
modulo una classe di resto (il numero di
litri d'acqua nel recipiente medio). Ripetendo le operazioni
da capo, scorreremo tutte le classi di resto, e quindi avremo
anche a un certo punto il valore N cercato.
Francesco Veneziano
Sia A il recipiente principale, B il maggiore dei recipienti
secondari, e C il più piccolo, siano (k+1)x+q, kx+q e x le
rispettive capacità dei recipienti (si assume che le capacità
siano espresse da un numero intero, o al massimo razionale).
Descriviamo la seguente strategia:
A>>B
B>>C
C>>A
B>>C
Dove gli ultimi due passaggi devono essere ripetuti sino allo
svuotamento di B
Verifichiamo dove ci porta questa strategia:
(k+1)x+q......0......0
x......kx+q......0
x......(k-1)x+q......x
2x......(k-1)x+q......0
2x......(k-2)x+q......x
3x......(k-3)x+q......0
Dopo k passaggi
(k+1)x......q......0
(k+1)x......0......q
Ripetiamo ora la stessa sequenza di mosse, questa ci porta a
(k+1)x-q......2q......0
(k+1)x-q......0......2q
Ripetuta a volte
(k+1)x-(a-1)q......aq......0
(k+1)x-(a-1)q......0......aq
Se il nostro "bersaglio" [(k+1)x+q]/2 è un
multiplo di q, prima o poi lo raggiungeremo in questo modo,
altrimenti, arriveremo ad un punto in cui il recipiente C non
sarà più in grado di contenere i multipli di q che
dovrebbero essere travasati, in particolare se x=jq-r
Si arriverà alla situazione
(k+1)x-(j-1)q......jq......0
(k+1)x-(j-1)q......r......jq-r
(k+1)x+q-r......r......0
(k+1)x+q-r......0......r
Ora lo scarto è di r, e ripetendo la procedura più volte
otterremo in successione tutti i multipli di r, se il "bersaglio"
è tra questi, lo raggiungeremo, altrimenti il recipiente C
non sarà più in grado di contenere i multipli di r che
dovrebbero essere travasati, in particolare se q=nr+t...
Ormai l'avrete sicuramente riconosciuto, è proprio lui,
l'algoritmo euclideo per il calcolo del massimo comun
divisore!
Infatti abbiamo cominciato con esprimere A e B come multipli
di x più un certo resto q, quindi abbiamo espresso x come
multiplo di q più un certo resto r, quindi q come multiplo
di r più un certo resto t, e così via sino ad arrivare a 1
se i volumi di B e C sono primi tra loro, o al loro MCD
altrimenti; se per un malaugurato caso i volumi fossero
irrazionali il processo di divisione andrebbe avanti all'infinito,
ed otterremmo approssimazioni razionali sempre migliori (credo
siano i convergenti della frazione continua).
Franco Cocca
Non sempre i travasi conducono a dividere in due
parti uguali il liquido.
Consideriamo la terna [2N,a,b] indicante le capacità dei tre
recipienti tali che
a+b=2N
All'inizio la situazione del liquido è
[2N,0,0]
Travasando il liquido fino "all'orlo" nei
recipienti si può riuscire ad ottenere nel recipiente di
capacità maggiore di N la combinazione lineare del tipo
m b - n a con m e n naturali
Affinchè tale quantità sia pari a N bisogna che
Esiste m apparten. Z , Esiste k apparten. Z : mb- ka=N
Moltiplicando l'equazione per 2 e ricordando che a+b=2N
2mb- 2ka=2N=a+b
e pertanto
(2m- 1)b=(2k+1)a (*)
Tale uguaglianza, per sussistere, essendo 2m- 1 e 2k+1
entrambi dispari, dovrà avere a e b, ridotti ai minimi
termini, entrambi dispari.
Ecco perché la terna [10,6,4] non permette la suddivisione
in [5,5,0]: 6 e 4 ridotti diventano 3 e 2 e il secondo
termine è pari.
Se invece a e b sono dispari la (*) è verificata quando
2m- 1=a
2k+1=b
e quindi quando
m=(a+1)/2
k=(b- 1)/2.
![]()
247. La scimmia e le noci di cocco (difficile)
di Alessandro89
Cinque marinai naufragano su un'isola semideserta (semi-,
perché c'è una scimmia).
Durante la giornata raccolgono un mucchio di noci di cocco,
per dividersele tra di loro il giorno dopo.
Durante la notte, però, uno si sveglia e decide di prendersi
la sua parte in anticipo: fa cinque mucchi uguali, vede che
avanza una noce, la dà alla scimmia e nasconde la sua parte.
Il secondo marinaio si sveglia poco dopo, va al mucchio (più
piccolo) e fa esattamente la stessa cosa: anche stavolta
rimane una noce per la scimmia.
Lo stesso fanno a turno gli altri tre: tutte le volte avanza
una noce per la scimmia.
Il mattino dopo, tutti vedono che il mucchio è più piccolo,
ma avendo la coscienza sporca stanno zitti. Fanno la
divisione, e di nuovo avanza una noce data alla scimmia.
Qual è il numero minimo di noci che i marinai avevano
raccolto?
Nota storica.
Questo problema è stato pubblicato (per la prima volta?) da
Ben Ames Williams in The Saturday
Evening Post nel 1926 e più
recentemente ripreso da Martin Gardner nel libro Enigmi e
giochi matematici 2°.
>>> Risposte & riflessioni
Riccardo
Innazitutto sono partito dal presupposto che il
numero iniziale debba avere obbligatoriamente 6 oppure 1 come
cifra delle unità.
Infatti il Numero stesso, diminuito di 1 (noce di cocco per
la scimmia), dev'essere divisibile per 5.
Non riuscendo ad impostare formule particolari che conducano
ad un risultato accettabile, ho proseguito per tentativi.
Ho notato che con un numero che ha come terna più a destra (centinaia,
decine e unità) 246 si andava oltre le tre possibilità di
suddivisioni consecutive (mentre con gli altri numeri testati
si arrivava massimo a tre suddivisioni consecutive).
Così facendo ho trovato 31246 che dà la possibilità di
giungere fino alla sesta ed ultima spartizione, con la noce
di cocco per la scimmia in tutte le suddivisioni.
Non so però se c'è un numero inferiore che dà le stesse
possibilità, perchè mi sono fissato a seguire la traccia
del 246.
La domanda di Riccardo
trova una risposta nel pregevolissimo intervento di Dino e
Ivana.
In sintesi: il numero più basso è 15621.
Dino e Ivana Niccolai
Indicando con n il numero di noci di cocco
complessivamente raccolte dai cinque marinai durante il
giorno, nella prima spartizione ogni gruppetto sarà formato
da:
a = (n - 1)/5
noci di cocco. Quando si sveglia il secondo marinaio non troverà più n noci di cocco, bensì un numero più piccolo: 4·a. Egli effettuerà una nuova suddivisione in altri cinque gruppetti ognuno composto stavolta da:
b = (4·a - 1)/5
noci di cocco. Sostituendo il valore di a precedentemente trovato si ottiene:
b = (4·n - 9)/25
Ripetendo lo stesso ragionamento per il terzo marinaio si ha:
c = (4·b - 1)/5 = (16·n - 61)/125
per il quarto:
d = (4·c - 1)/5 = (64·n - 369)/625
e per il quinto:
e = (4·d - 1)/5 = (256·n - 2101)/3125
Quando tutti si svegliano il giorno dopo effettuano un'ultima ripartizione per cui:
f = (4·e - 1)/5 = (1024·n - 11529)/15625
Questa equazione prende il nome di equazione diofantea perchè deve essere soddisfatta da valori di f ed n interi: Infatti il numero minimo di noci raccolte dai marinai non si ottiene impostando f = 1, cioè con l'ultima spartizione di un solo cocco a testa in quanto si otterrebbe un valore di n non intero! Occorre cercare allora quel valore minimo di f tale che anche n sia intero. La soluzione di questa equazione può essere trovata per tentativi, ma il procedimento é molto lungo. Facendo un ragionamento a ritroso però da f possiamo scrivere:
e = 5·f + 1
quindi:
d = e + 1 + e/4
Questo significa che e oltre ad essere intero deve essere anche multiplo di quattro, e per la precedente anche f, a meno di uno, deve essere multiplo di quattro. Continuando a ritroso si ha:
c = d + 1 + d/4
cioè anche d deve essere multiplo di quattro, ma ciò comporta che allora e deve essere multiplo di 16 ed f, sempre a meno di uno, anch'esso multiplo di 16. Per b, a, ed n possiamo ragionare analogamente:
b = c + 1 + c/4
a = b + 1 + b/4
n = a + 1 + a/4
In definitiva a è un multiplo di quattro, b multiplo di 16, c multiplo di 64, d multiplo di 256, e multiplo di 1024, ed f, sempre a meno di uno, ancora multiplo di 1024. Il primo valore di f valido è pertanto 1023.
Infatti, impostando tale valore nell'equazione diofantea si ottiene il valore più piccolo per n che risulta essere 15621.
Esiste anche una semplice ed elegante soluzione, che coinvolge il concetto di "noce negativa" per risolvere l'equazione diofantea. Osserviamo innanzitutto che, poichè il numero da trovare viene diviso sei volte per cinque, ogni risposta accettabile, se sommata a 56 = 15625, ci dà la risposta successiva di ordine superiore. E' ovvio che non esiste un numero n positivo piccolo che soddisfi all'equazione (basta fare qualche tentativo per accorgersene), ma é possibile che ve ne sia uno piccolo negativo: infatti se il marinaio si avvicina al mucchio composto da -4 noci ed in prima battuta aggiunge e sottrae una noce di cocco il risultato non cambia. In tal modo si otterranno -5 noci più una reale (positiva); regala quest'ultima alla scimmia ottenendo un mucchio formato ora da -5 noci. Lo divide per cinque e si prende -1 noce. Resta nuovamente il mucchio con -4 noci. Il secondo marinaio ripete lo stesso procedimento, una noce positiva tocca sempre alla scimmia, -1 noce a lui e ne restano ancora -4. Il procedimento si reitera per tutti i marinai, lasciando invariato il numero di noci dopo la divisione (sempre -4). In questo modo, infatti, i marinai non devono fare che sottrarre e aggiungere ogni volta una noce al mucchio originario per ottenere un'equa divisione dei beni (equa sì, ma svantaggiosa per tutti). Alla mattina dunque, lasciata una noce positiva alla scimmia, ogni marinaio si prende una noce negativa. Risultato: ciascun uomo ha -2 noci e la scimmia possiede 6 noci. Dunque n = -4 è una soluzione dell'equazione diofantea, ma ovviamente non è accettabile fisicamente. Basta però sommarvi 15625 per ricavare immediatamente la soluzione di ordine superiore: -4 + 15625 = 15621. Con questo risultato si può osservare che l'ultima divisione lascia ancora 1023 noci a ciascun marinaio. D'altra parte esiste anche un teorema che dice che se X e Y sono le soluzioni di un'equazione diofantea di forma A·x - B·y = C, allora un'altra soluzione è data da X + B e Y + A, cioè, in questo caso proprio da 15621 (= -4 + 15625) e 1023 (= -1 + 1024).
Per capire meglio il concetto di noce negativa Norman Anning del dipartimento di matematica dell'Università del Michigan nel 1912 ragionò nel seguente modo: quattro noci delle 56 vengono tinte di nero e messe da parte. Quando le rimanenti vengono divise per cinque ne rimane una che viene data alla scimmia. Dopo che il primo marinaio ha preso la sua parte e la scimmia ha avuto la sua noce, rimettiamo di nuovo le quattro noci nere con le altre in modo da averne un mucchio di 55 noci, evidentemente divisibile per cinque, però prima di fare la successiva divisione mettiamo di nuovo da parte le quattro noci nere in modo che dalla divisione rimanga una noce da dare alla scimmia. Questo procedimento di prendere in prestito le noci nere solo quanto basta per vedere che si può effettuare una divisione per cinque e poi metterle da parte viene ripetuto a ogni divisione. Dopo la sesta divisione, le noci nere rimangono da parte e non sono più di nessuno. Esse non hanno una parte essenziale nell'operazione, ma servono solo a rendere le cose più chiare nel procedere.
E' possibile effettuare la generalizzazione del problema delle noci di cocco: sia M il numero dei marinai, maggiore di due, detti X il numero totale di noci raccolte dai marinai ed Y il numero di noci distribuite a ciascuno alla fine risulta:
X = [K·M(M + 1)] - (M - 1) Y = [K·(M - 1)M] - 1
dove K è un numero intero positivo che, posto uguale a 1, fornisce i valori minimi cercati nel problema. Se il numero di noci di cocco date alla scimmia alla fine di ogni tornata è pari ad N, con N qualsiasi intero maggiore di uno, si ha invece:
X = [K·M(M + 1)] - N·(M - 1) Y = [K·(M - 1)M] - N
Sprmnt21
Volevo solo riscrivere in maniera leggermente diversa quello
gli altri hanno gia' scritto sul problema delle noci di rocco.
Indico con n e con x1, x2, ..., x5 il numero di noci di cocco
raccolte e quello che ognuno durante la notte sottrae e con x6
il numero di noci di cocco che spetta ad ognuno dopo la
divione mattutina.
Si ha in successione che:
n = 5 x_1+1
4 x_1 = 5 x_2+1
4 x_2 = 5 x_3+1
4 x_3 = 5 x_4+1
4 x_4 = 5 x_5+1
4 x_5 = 5 x_6+1
Sommando 4 ad ambo i membri delle precedenti uguaglianze, si
ottiene:
n + 4 = 5(x_1+1)
4(x_1+1) = 5(x_2+1)
4(x_2+1) = 5(x_3+1)
4(x_3+1) = 5(x_4+1)
4(x_4+1) = 5(x_5+1)
4(x_5+1) = 5(x_6+1)
da cui, "moltiplicando tutte le uguaglianze", si
ricava che
(n+4)4^5 = 5^6(x_6+1).
dato che ne' il 5 ne' alcuna sua potenza compare come fattore
di 4^5, si ha che n+4 e' multiplo di 5^6. Il piu piccolo
valore che risponde al problema e' percio' n = 5^6-4.
Sprmnt21
Ancora sulle noci di cocco, per sottolineare che
quello che e' essenziale alla natura del problema, non e' il
numero totale (5) di naufraghi o il numero di questi che
"prelevano" durante la notte, prima della
spartizione alla luce del sole, ma, in un certo senso, il
fatto che ci sia una sola scimmia nell'isola ;-).
Infatti siano n, k ed h il numero di noci di cocco
raccolte il numero di naufraghi e il numero di "nottambuli"
rispettivamente. Indicate con x_1, x_2, ..., x_h quello che
ognuno durante la notte sottrae e con x_{h+1} il numero di
noci di cocco che spetta ad ognuno dopo la divione mattutina.
Si ha in successione che:
n = k x_1+1
(k-1) x_1 = k x_2+1
(k-1) x_2 = k x_3+1
..
(k-1) x_h = 5 x_{h+1}+1
Sommando k-1 ad ambo i membri delle precedenti uguaglianze, e
"moltiplicando tutte le uguaglianze", si ricava che
(n+k-1)(k-1)^h = k^(h+1)(x_{h+1}+1).
essendo k e k-1 coprimi, si ha che n+k-1 e' multiplo di k^(h+1).
Il piu piccolo valore che risponde al problema e' percio' n'
= k^(h+1)-k+1.
![]()
246. Trasformazione di serie
di Cesarone
Trovate la legge che trasforma la serie:
... 45 55 66 78 91 105 120 ...
nella serie:
... 45 50 56 60 67 70 78 ...
>>> Risposte & riflessioni
Paolo P.
A guardare le due successioni ho pensato, indicando con An i
numeri della prima (A0=45, A1=55, A2=66, ...) e con Bn i
numeri della seconda (B0=45, B1=50, B2= 56, ...), di
calcolare (... audacemente) le differenze An - Bn = Dn.
Ho riscontrato che:
D0=0
D1=5
D2=10
D3=18
D4=24
D5=35
D6=42.
Dopo qualche tentativo, ho verificato che:
D1 = INT((A1-A0)/2) * 1
D2 = INT((A2-A1)/2) * 2
D3 = INT((A3-A2)/2) * 3
D4 = INT((A4-A3)/2) * 4
D5 = INT((A5-A4)/2) * 5
D6 = INT((A6-A5)/2) * 6
INT sta per Parte Intera ... e queste formule esprimono il
passaggio da An a Bn in funzione degli An stessi.
Coincide?
Dimenticavo: gli An dovrebbero essere della forma: An =
A0 + n*10 +
n*(n-1)/2 con A0 = 45
![]()
245. Nuove sequenze audioattive
di Cesarone
Ho provato a creare delle sequenze audio attive usando
altre regole...
Sicuramente qualcuno ci ha già provato... ma mi sembrano
interessanti.
Se leggo quanti 1 quanti 2 quanti 3 ecc. ecc. ci sono in una
sequenza (andando in ordine con le cifre che trovo), ottengo:
1
11
21
1211
3112 (perchè nella sequenza precedente compare 3 volte 1 e
una volta 2)
13212 (perchè compaiono un 3 due 1 e un 2 nella sequenza
prima)
211322
322113
232221
421311
14123113
41141223
24312213
32142321
23322114 ******
32232114
23322114 ******
In pratica mi fermo perchè torno sempre alla stessa sequenza!
Inoltre partendo con un simbolo qualsiasi mi pare che la
sequenza si blocchi ugualmente.
Se invece di andare in ordine con le cifre che trovo, seguo
tutte le volte l'ordine 1, 2, 3, 4, cioè dico prima quanti 1
poi quanti 2 poi quanti 3 poi quanti 4, ottengo:
1
11
21
1112 (nella sequenza prima ho un 1 e un 2)
3112
211213 (nella sequenza prima ho due 1 un 2 e un 3)
312213
212223
114213
31121314
41122314
31221324
21322314 *******
21322314 *******
......
Mi fermo perchè ottengo una combinazione da cui non mi
sposto più!
>>> Risposte & riflessioni
![]()
244. Altre lampadine da accendere
di Riccardo
Da cosa nasce cosa... e
Riccardo, nel tentativo di risolvere la ricreazione 242.
Una scacchiera 4x4 di Ivana Niccolai e
Dino, ha avuto un'idea...
Mi è tornato alla mente un
quesito analogo che vorrei proporre tra le ricreazioni.
Si hanno 25 lampadine spente disposte in 5 righe e 5 colonne
e ogni lampadina è collegata ad un proprio interruttore.
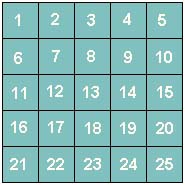
Manovrando un interruttore si inverte lo stato della lampadina collegata (se è spenta si accende e viceversa) e contemporaneamente si inverte lo stato delle lampadine adiacenti (orizzontalmente e verticalmente, ma non obliquamente). Ad esempio, manovrando l'interruttore n.12 si avrà la seguente situazione:
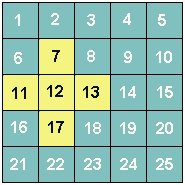
manovrando poi l'interruttore n.13 si avrà la seguente situazione:
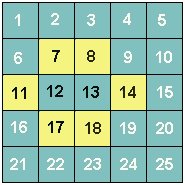
(Le lampadine 12 e 13 si spengono perchè erano accese e le lampadine 8, 14 e 18 si accendono perchè erano spente) si deve giungere ad accendere tutte le lampadine.
Le soluzioni sono diverse, ma qual è la sequenza più breve di interruttori da manovrare?
>>> Risposte & riflessioni
Francesco Veneziano
Bisogna capire che succede se si aziona un
interruttore collegato ad una delle lampadine del bordo, o
degli angoli; la cosa più naturale è che si considerino i
bordi collegati tra loro (superiore-inferiore e destro-sinistro)
così che, ad esempio, azionando la lampadina 3 le lampade
coinvolte sono 2-3-4-8-23 ed azionando la 1, sono 21-5-1-2-6.
Se le cose stanno così, basta premere tutte le lampadine una
volta, indipendentemente dall'ordine, così ogni
lampadina è azionata 5 volte (1 volta lei, e 4 volte dai
vicini) e rimane accesa.
Questa soluzione è valida qualunque sia il lato del
quadrato, ma è migliorabile se consideriamo il caso
particolare proposto da Riccardo, infatti selezionando 5
caselle disposte a "passo di cavallo" 1-8-15-17-24
tutte le lampadine del quadrato vengono azionate soltanto una
volta; naturalmente non si può fare di meglio.
![]()
243. Copertura del quadrato
di Paolo P.
Dovete inserire un triangolo e 2 cerchi in un
quadrato di lato unitario.
Qual' è la superficie massima che riuscite a coprire ?
>>> Risposte & riflessioni
Pietro Vitelli
La superficie massima, in un quadrato, che è possibile
ricoprire con un triangolo e due cerchio, è, con precisione
fino all'ottava cifra decimale: 93,07756449 %.
Vi mostro il perchè:
Innanzitutto la figura:
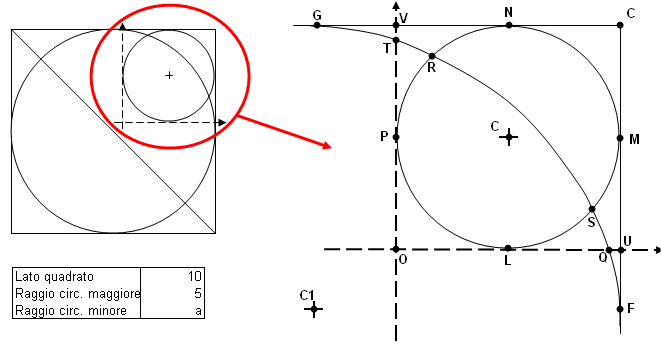 Le
mie posizioni:
Le
mie posizioni:
Circonferenza maggiore di centro C1:
C1(-1,-1)
raggio r1=5 (il diametro è 10 cosicchè l'area del quadrato
risulta uguale a 100, in modo tale da avere subito la
percentuale di area ricoperta)
Circonferenza minore di centro C:
C(a,a)
raggio r=4-a
Ricaviamo le equazioni delle due circonferenze:
eq. circ. maggiore:
(x+1)²+(y+1)²=5² da cui
x²+y²+2x+2y-23=0
eq. circ. minore:
(x-a)²+(y-a)²=(4-a)² da cui
x²+y²-2ax-2ay+a²+8a-16=0
A questo punto per il calcolo dell'area RNMS sono necessari i
punti R, S ed M;
M è chiaramente uguale a:
M(4,a)
Per calcolare R ed S, invece, dobbiamo intersecare le due
circonferenze:
x² + y² + 2x + 2y - 23=0 x² + y² - 2ax - 2ay + a² + 8a - 16=0 --------------------------------------------- // // (-2a-2)x + (-2a-2)y + a² + 8a + 7=0
da cui y= -x +(a²+8a+7)/(2a+2)
Andiamo ora ad intersecare tale retta con la circ. minore:
***
* x²+y²-2ax-2ay+a²+8a-16=0
* y= -x +(a²+8a+7)/(2a+2)
***
da cui si ottiene la seguente equazione di 2° grado:
8x²-4(a+7)x+a²+18a-15=0
la cui soluzione, calcolata con l'aiuto di derive è:
x=(a+7±rad(-a²-22a+79))/4
per cui:
R( (a+7-rad(-a²-22a+79))/4, -(a+7-rad(-a²-22a+79))/4 + (a²+8a+7)/(2a+2))
S( (a+7+rad(-a²-22a+79))/4, -(a+7+rad(-a²-22a+79))/4 + (a²+8a+7)/(2a+2))
A questo punto ho calcolato l'area RNMS come differenza di
integrali, e cioè:
Integrale[R,S](circ.minore)-Integrale[R,S](circ.maggiore)-Integrale[S,M](circ.minore);
ovviamente le equazioni delle due circonferenze devo essere
esplicitate rispetto ad una variabile; ecco:
eq.circonferenza maggiore, di centro C1:
y=-1±rad(-x²-2x+24)
(per il calcolo dell'integrale c'è bisogno della sola
equazione della semicirconferenza superiore)
eq.circonferenza minore, di centro C:
y=a±rad(-x²+2ax-8a+16)
(serviranno entrambe le equazioni delle due semicirconferenze
per il calcolo degli integrali).
Andiamo proprio a calcolare gli integrali:
Area(RNMS)=Integrale[R,S](circ.minore)-Integrale[R,S](circ.maggiore)-Integrale[S,M](circ.minore)
Risolviamo ciascun integrale singolarmente:
Integrale[R,S](circ.minore)
Integrale[R,S](a+rad(-x²+2ax-8a+16))
(il segno + nell'integrale c'è perchè si tratta della
semicirconferenza superiore)
La soluzione indefinita, trovata sempre con l'aiuto di
derive, è:
(a²-8a+16)*ARCSIN((x-a)/ABS(a-4))/2+(x-a)*RAD((4-x)*(x-2(a-2)))/2+ax
Integrale[R,S](circ.maggiore)
Integrale[R,S](-1+rad(-x²-2x+24))
La soluzione indefinita è:
25*ARCSIN((x+1)/5)/2+(x+1)*RAD(-x²-2(x-12))/2-x
Integrale[S,M](circ.minore)
Integrale[S,M](a-rad(-x²+2ax-8a+16))
(stavolta il segno nell'integrale è - perchè l'integrale
interessa la semicirconferenza inferiore)
La soluzione indefinita è:
-(a²-8a+16)*ARCSIN((x-a)/ABS(a-4))/2+(a-x)*RAD((4-x)(x-2(a-2)))/2+ax
Dopo aver calcolato questi integrali ho riportato i loro
valori in funzione di a, nonchè i valori dei punti R ed S,
anch'essi in funzione di a, in un foglio di calcolo di Excel.
Sul foglio ho fatto in modo che i valori di punti e integrali
fossero collegati ad una cella all'interno del quale poteva
essere inserita l'ascissa del centro C;
in questo modo ad ogni immissione del centro C si avevano
opportuni valori per i punti, gli integrali, e l'area RNMS,
cosicchè, per ogni valore del centro inserito, si aveva la
percentuale di area coperta.
Dopo una decina di tentativi ho trovato l'area massima
ricopribile, con precisione fino ad 8 cifre decimali e cioè:
93,07756449 %.
(uff!che faticata)
![]()
242. Una scacchiera 4x4
di Ivana Niccolai e Dino
In una scacchiera quattro per quattro sono
sistemate 16 lampadine, ognuna nella rispettiva casella.
Una di esse è spenta mentre tutte le altre sono accese.
| a | b | c | d | |
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 |
La lampadina b3 spenta è solo un esempio
E' possibile cambiare in un sol colpo lo stato delle lampadine (accese/spente) di tutte le caselle di una riga o di una colonna tramite un interruttore ben identificabile (ad esempio, se la colonna tre è tale di avere la sequenza accesa-accesa-spenta-accesa, può diventare con una sola manovra sull'interruttore colonna tre spenta-spenta-accesa-spenta).
Qual è la sequenza di manovre sugli interruttori più breve per rendere tutte le lampadine accese con nessuna spenta?
>>> Risposte & riflessioni
Jack202
A) Configurazione iniziale : tutte lampadine accese,
una spenta
B) Configurazione finale : tutte accese
Poichè si tratta solo di operazioni di switch binario, non
conta l'ordine in cui vengono fatte le mosse allo scopo di
ridurre A) in B)
Se consideriamo ogni switch colonna/riga come il
piazzamento di un rettangolo formato da 4 quadratini lungo la
colonna/riga, alla fine delle nostre mosse dovremo avere un
numero pari di quadratini che coprono ogni casella tranne
quella inizialmente spenta, che dovrà avere un numero
dispari di quadratini sopra. I quadratini piazzati sulla
scacchiera saranno quindi in totale un numero DISPARI.
Ma ogni rettangolo ha contribuito con il piazzamento di un
numero PARI di quadratini, dunque NON è POSSIBILE
passare da A) a B).
Ivana Niccolai e Dino
Non è mai possibile rendere tutte le lampadine
accese o, viceversa, tutte spente!
Infatti, posta la convenzione che ogni lampadina accesa vale zero e ogni lampadina spenta vale uno, se tutte le lampadine sono accese, come si vorrebbe, la somma dello schema che si verrebbe a formare sarebbe sempre pari a zero, altrimenti, se tutte sono spente sarà sedici. Quando si inverte lo stato delle lampadine di un'intera riga, o una intera colonna, si può avere solo uno dei seguenti cinque casi:
Prima della manovra |
Somma |
Dopo la manovra |
Nuova somma |
||||||
1 |
1 |
1 |
1 |
4 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
3 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
2 |
0 |
0 |
1 |
1 |
2 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
3 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
4 |
Da tale tabella notiamo che un qualsiasi cambiamento non muta mai la PARITA' del totale: da pari prima della trasformazione si va sempre in pari dopo la stessa mentre da dispari si va sempre in dispari. Quindi, con una sola lampadina spenta in tutta la scacchira il totale è pari ad uno, ovvero dispari, e non si potrà mai arrivare ad avere tutte le lampadine accese o spente, rispettivamente con totali pari a zero e sedici, che sono entrambi pari!
![]()
241. La bilancia "sbilanciata"
di Gianfranco Bo (variante ad un
problema di Jesus Escudero Martin)
Carletto ha costruito una bilancia a due piatti.
La bilancia sembra funzionare perfettamente, però un
oggetto se viene messo sul piatto destro pesa 10 g
mentre se viene messo sul piatto sinistro pesa 9 g.
Quante e quali potrebbero essere le cause dello "sbilanciamento"?
Quanto peserebbe in realtà l'oggetto in ciascuno dei casi?
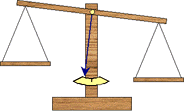
>>> Risposte & riflessioni
Può essere sbilanciata perché:
a) un piatto è più pesante dell'altro; (9,5 g)
b) i bracci della leva sono di lunghezza diversa; (9,49 g)
c) la base non è perfettamente orizzontale;
d) ...
Caso a)
Chiamiamo p il peso vero dell'oggetto.
Supponiamo che un piatto (il destro) pesi x più dell'altro.
1° pesata: 10 = x + p
2° pesata: p = 9 + x
da cui, sottraendo:
10 - p = x + p - 9 - x
2p = 19
p = 9,5
Che è la media dei due pesi.
Tra parentesi: si può anche calcolare la differenza di peso
fra i piatti
x = p - 9 = 0,5 g
Caso b)
Alessandro Venturi
La situazione è la seguente:
P----a----F--------b--------5
9----a----F--------b--------P
dove F è il fulcro della bilancia, P il peso incognito, a, b le misure dei bracci.
Se indico con:
P (peso incognito)
a (braccio corto)
b (braccio lungo)
k<1 a/b (rapporto tra i bracci)
P*a = b*9
P*b = a*10
Questo sistema che impone l'ugualianza dei momenti dei due
bracci consente di risolvere il problema.
P = 9/k
P = 10*k
Ricavo k
10k = 9/k
10k^2 = 9
k = +-sqrt(9/10)
Ricavo P (sostituendo il valore positivo di k)
P = 10*sqrt(9/10) = 9,49 g
![]()
Sito Web realizzato da Gianfranco Bo